新型高分辨率自然伽马测井仪器的优化设计与资料处理技术
陶宏根,商庆龙,刘长伟,汪宏年,李舟波
1.吉林大学地球探测科学与技术学院,长春 130026 2.大庆钻探集团测井公司,黑龙江大庆 163412 3.吉林大学物理学院,长春 130012
新型高分辨率自然伽马测井仪器的优化设计与资料处理技术
陶宏根1,2,商庆龙3,刘长伟2,汪宏年3,李舟波1
1.吉林大学地球探测科学与技术学院,长春 130026 2.大庆钻探集团测井公司,黑龙江大庆 163412 3.吉林大学物理学院,长春 130012
通过自然伽马响应函数与其探测器长度间关系的研究,选择长度为0.1m的NaI晶体作为新型高分辨率自然伽马仪器的探测器。为克服短NaI晶体会导致计数率降低和统计涨落误差增大等问题,利用4个大小完全相同的NaI晶体同时测量伽马射线强度,获得4条高分辨率自然伽马测井曲线;然后,对4条测量曲线进行累加并结合带通滤波技术充分降低统计涨落误差;在此基础上,进一步应用正则化反褶积处理提高仪器的纵向分辨率。理论模型和井场试验结果均证明,该新型高分辨率伽马仪器具有0.15m的纵向分辨率,比常规自然伽马测井仪器的分辨率提高了4倍以上。
自然伽马;测井;高分辨率;带通滤波;正则化反褶积
Key words:nature Gamma-ray;well logging;high vertical resolution;low-pass filter;regularized deconvolution
0 引言
由于放射性本身具有统计涨落效应,为提高测量效率并保证测量精度,自然伽马仪器往往采用长度较大的柱状NaI晶体作为探测器,其直径和长度分别是0.05m和0.325m,其纵向分辨率大约为0.6m。提高其纵向分辨率需要采用反褶积等高分辨率处理技术[1-2]。由于自然伽马仪器响应存在盲频,高分辨率处理能够得到的最大纵向分辨率大约为0.3m[3-4]。
大庆油田目前已进入后期开发阶段,如何保持稳产并延长其开采寿命,需要不断挖掘老油田中薄差层的油气潜力;因此,研制开发新的高分辨率仪器和高分辨率处理技术来满足薄差层解释评价的需要,已成为大庆测井公司重要的工作目标。过去10余年中,在高分辨率处理与电测井资料反演等方面开展了大量的合作研究[3-10],测井公司已建立了独立的高分辨率快速测井平台。目前正在研究开发0.2m纵向分辨率的系列测井仪器,包括自然伽马、中子、密度、三侧向等主要测井方法,为油田中薄差层准确识别和有效开发提供准确资料,为大庆油田持续稳产提供技术支撑。
笔者主要介绍在新的高分辨率自然伽马仪器研制过程中,在仪器参数优化设计与资料处理方面的主要研究成果。首先通过考察仪器响应函数与其探测器长度间的关系,选择长度只有0.1m的NaI晶体作为新型高分辨率自然伽马仪器的探测器。为提高测量精度和效率,在整个井下仪器中设置4个尺寸完全相同、彼此相互分离的NaI晶体并同时进行测量、提供4条完全相关的高分辨率自然伽马测井曲线。由于存在统计涨落误差,同时测量到的这4条伽马测井曲线往往存在较大差异;为此,采用曲线累加、带通滤波等资料合成技术充分降低统计涨落误差对观测结果的影响,获得分辨率相对较高的自然伽马测井曲线。在此基础上,进一步应用正则化反褶积处理提高仪器的纵向分辨率。最后通过理论模型和井场试验结果对该新型高分辨率伽马仪器的探测特性进行检验,证明该仪器能够达到大约0.15 m的纵向分辨率。
1 探测器长度选取与提高测量精度的措施
直接利用文献[1,3]的结果,可以得到探测器长度为L(m)、采样间距为Δ(m)、测速为v(m/s)的自然伽马仪器的空间域纵向响应函数的表达式:
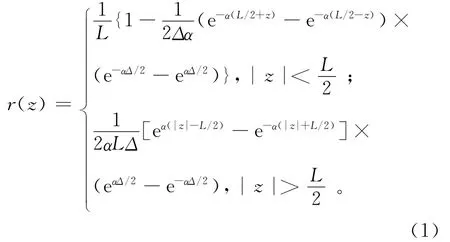
其中:α是伽马射线在地层中的衰减常数;z为垂直方向的坐标。对式(1)进行傅里叶变换,得到响应函数在频率域中表达式:
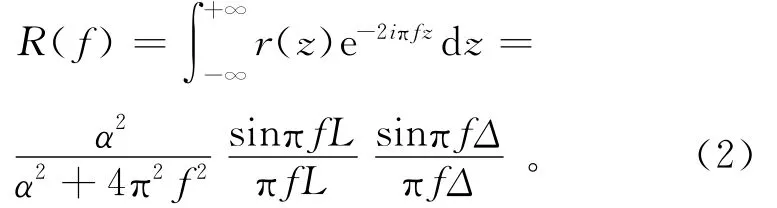
式中,f为空间频率(Hz)。
由于当f=±1/L和f=±1/Δ时,R(f)=0,所以自然伽马测井响应存在盲频问题;不难推断,自然伽马仪器的纵向分辨率将与探测器长度L和采样间距Δ有关。图1是探测器长度分别为0.05、0.08、0.1、0.2、0.4m,采样间距为0.02m情况下,由式(1)和式(2)计算得到的空间域和频率域响应函数。其中,衰减常数α值为7.45,该值由刻度井测量结果经最佳拟合得到(见后面的数值结果)。结果显示:0.05、0.08、0.10m的3个较短探测器,对应的空间域和频率域的响应函数均相差较小;但当探测器长度达到0.2m后,长度增加导致空间响应函数明显变宽和频率域响应函数的频带也明显变窄,表明其纵向分辨率也越低。需要指出的是,探测器在单位时间内接收到的伽马粒子数与其长度成正比,探测器越长,其接收伽马粒子的几率也越大,相应计数率U也越高。放射性元素的衰变满足Possion统计规律,计数率误差(变差)为槡U、相对误差为;因此,计数率越高,统计涨落影响也越小。
综上所述,探测器分辨率与其探测精度是相互制约的:如果探测器短,分辨率会提高,但其测量精度会降低(除非降低测量速度)。为此,选择0.10m的NaI晶体作为探测器,以保证仪器具有足够高的纵向分辨率。为有效保证测量效率和精度,在整个井下仪器中设置4个尺寸完全相同、彼此相互分离的NaI晶体并同时进行测量,获得4条不同的自然伽马测井曲线,通过简单的深度平移、计数率平均等合成技术计算出一条自然伽马测井曲线。这样不仅保证了自然伽马测井记录的纵向分辨率,也提高了每个深度点上探测器的总计数率,有效提高了测量精度。
2 自然伽马测井响应与资料处理
如果用u(z)表示井轴上的自然伽马测井记录,用m(z)表示地层中伽马射线的发射强度,利用式(1)的纵向响应函数r(z)以及Possion统计规律,自然伽马测井记录可表示为
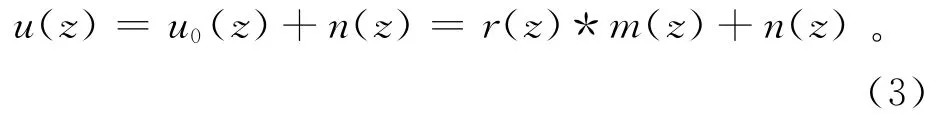
其中:u0(z)=r(z)*m(z)是自然伽马测井记录的希望值;n(z)为测井记录中的随机噪声。而且,


由于统计涨落效应,同一探测器在同一位置的不同时间内测量到的自然伽马记录往往不同。模拟0.1m长的4个相同探测的含有噪声的理论测井响应,以便研究噪声消除方法。利用随机数发生器产生一个取值为1或-1的4个不同的随机数序列Ni,k,i=1,…,4,k=1,2,…,106,同时假设采样间距为Δ;这时在深度点zk=Δk上4个探测器的噪声可
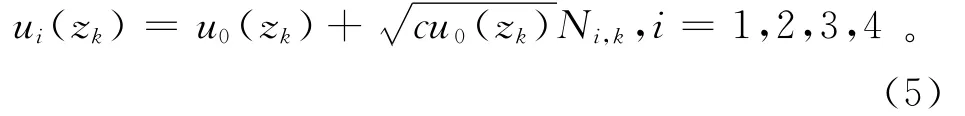
数据处理的主要目的是从含有Possion噪声的4条自然伽马测井记录ui(z),i=1,2,3,4中提取出可靠的自然伽马测井记录希望值u0(z)。为此,采用如下处理过程:
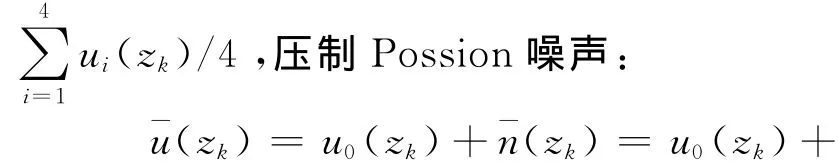
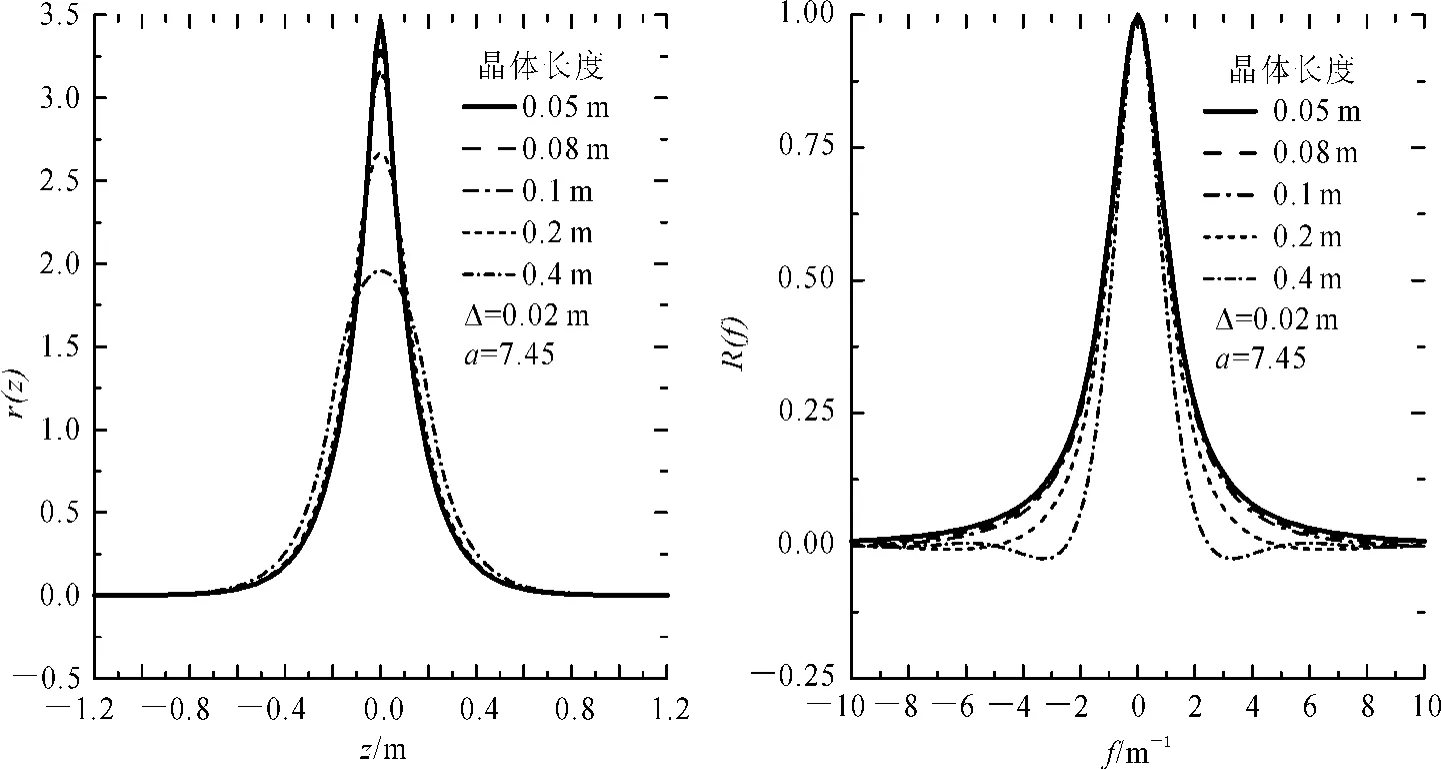
图1 不同长度的探测仪器在空间域和频率域的响应函数Fig.1 Response functions in both spatial and frequency domains of Gamma-ray detectors with variable lengths
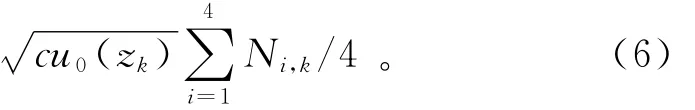
1)直接求4条测井曲线的平均值珔u(zk)=因Ni,k是取值为-1或1的随机数序列,故平均值是取值为0、±1/2和±1的随机数,且平均值等于0和±1/2的概率为7/8。因此,通过平均处理,式(6)中珔u(zk)的噪声珔n(zk)已经得到了有效压制,但噪声的平均值珔n(zk)仍然不完全等于零。
2)利用带通滤波器计算滤波测井曲线uf(z)=h(z)*珔u(z),进一步压制噪声珔n(zk),并用滤波曲线uf(z)作为新的自然伽马测井记录。由方程(2)给出的频率域中自然伽马测井仪器的响应函数R(f)的表达式不难推断,不含噪声的理想测井记录u0(z)是带限的,而噪声珔n(z)的频带肯定比u0(z)的频带宽。为有效压制高频噪声,利用文献[2]的结果引入频率域带通滤波因子:
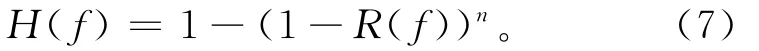
其中,n是正整数,通常取为5或6时就可以得到较满意的效果。
对式(7)求傅里叶逆变换确定空间域中的滤波因子h(z),即h(z)=F-1[H(f)],通过简单的褶积运算就可以得到滤波曲线uf(z)。
3)为进一步有效提高滤波测井曲线uf(z)=h(z)*珔u(z)的纵向分辨率,采用文献[3]中的正则化反褶积技术,利用下式先计算正则化反褶积因子
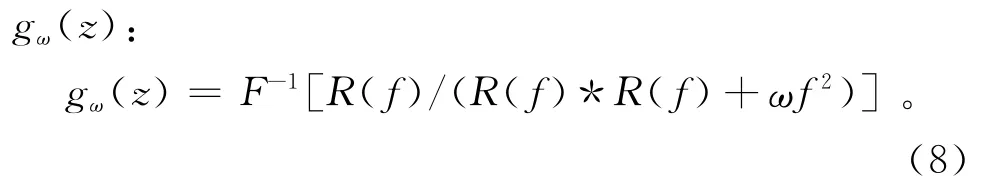
其中,ω是正则化反褶积因子。利用如下反褶积公式确定出高分辨率自然伽马曲线:
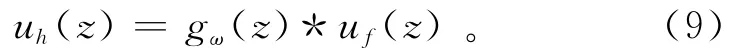
3 数值结果
3.1 自然伽马衰减常数α的确定
图2a是刻度井示意图,该刻度井由3个厚度分别为1.5、0.4、0.2m的高放层(放射性强度为223 API)以及一个厚度为0.4m和3个厚度分别为0.9 m的低放层(放射性强度为15API单位)组成,整个刻度井长度是5.2m。图2b中的GR0是半径和长度分别为0.05m和0.1m的单一圆柱状NaI晶体以60m/h测得的自然伽马测井记录(采样间距0.02m);因测速很慢,测井记录上的涨落效应已经很小。由于是试验性仪器且测速很低,同时测速误

极小化,确定衰减常数α以及刻度校正因子k′和b。得到α值为7.65,k′和b的值分别为0.976和10.419。图2b中,GRCOR是对原始记录GR0进行深度拉伸和按公式u′i=k′ui+b进行重新刻度后得到的结果,GRFWD是对应于α=7.56时的理论合成测井记录。可以看到,GRCOR和GRFWD吻合得非常好,也证明了褶积模型的正确性。
3.2 理论合成数据处理结果
图3a是新的高分辨率自然伽马仪器的理论合成响应,其中,GR1、GR2、GR3和GR4表示4个探测器上的合成测井记录。由于含有Possion噪声,4条测井记录均存在非常明显的起伏跳跃。模型由22个不同厚度的层状地层组成:上半部分由厚度依次为0.10、0.15、0.20、0.30、0.40、0.60m的低放层(放射性强度为55API)组成,且被厚度均为0.6m的高放层(放射性强度为223API)隔开;下半部分是厚度依次为0.6、0.4、0.3、0.2、0.1m的高放层被厚度均是0.6m低放层隔开。为压制图3a中各个曲线的噪声,先对每个深度上的GR1、GR2、GR3和GR4进行平均得到平均伽马曲线(GRAV),然后利用方程(7)的带通滤波器对GRAV滤波处理,得到滤波曲线GRFL。图3b给出了GRAV、GRFL以及不含噪声的理论合成曲线(GR0)的对比。不难看出:GRAV对伽马射线的起伏涨落效应有了非常明显的压制作用,但仍然存在较明显的起伏涨落现象;滤波曲线GRFL中的起伏涨落效应已得到更好地压制,与不含噪声的理论合成曲线GR0相差很小。
图3c是利用反褶积公式(9)对滤波曲线GRFL和理论合成曲线GR0进行高分辨率处理后的结果。结果证明,通过对伽马曲线进行平均、滤波以及高分差较大,导致测井记录存在着非常明显的深度偏差;需要对测井记录进行拉伸处理,以便与刻度井上的真实深度对齐。此外,低放层上的测井记录明显小于地层放射性强度真值mMOD,说明仪器的刻度也存在着一定的误差。
为确定方程(1)中的α,需要进行深度校正和测井记录的重新刻度。首先,选定高放层和低放层的中间位置zi(i=1,2,…,5),并读取深度校正各深度点上的测井记录ui(i=1,2,…,5);同时利用褶积模型u0(z,α)=r(z,α)*m(z)计算测井记录的希望值,然后通过对目标函数辨率处理,新的高分辨率自然伽马仪器纵向分辨率得到明显提高,对于0.1m的薄层仍然有非常明显的反应,且与无噪声GR0的反褶积结果基本相同,说明整个处理具有较强的抗噪能力。
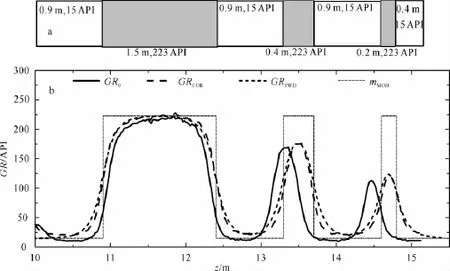
图2 刻度井上的测量结果与理论合成数据对比Fig.2 Comparison between the measurement results and synthetic logs in the calibration well
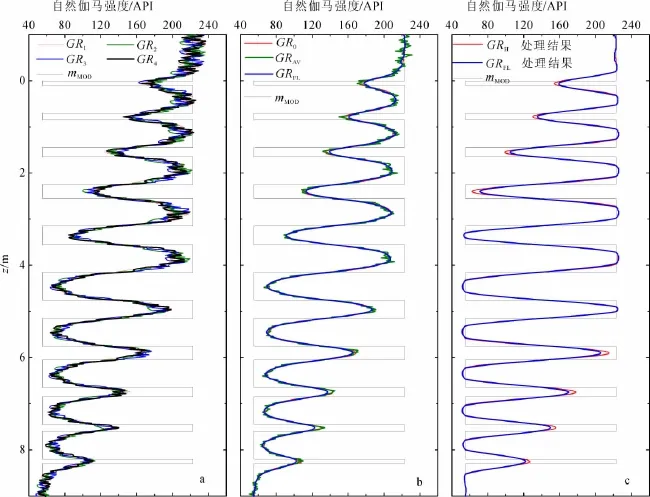
图3 理论合成数据与资料处理结果Fig.3 Synthetic Gamma-ray logs and process results
3.3 井场试验数据的处理结果
为检验新的高分辨率伽马仪器的实际测量效果,利用研制出的一台样机在井场进行了试验。这里给出原始测量数据、处理结果以及与其它测井记录的对比情况。
图4是新的自然伽马仪器在大庆某井上测量得到的原始测量数据、处理结果以及与其它测井记录的对比。其中,图4a是4个探测器同时测量得到的自然伽马计数率(U1、U2、U3和U4),由于计数率已经被转化成电信号,其单位为mV。该仪器的仪器常数c为0.575,将计数率乘以仪器常数得到自然伽马强度(API)。图4b是对原始计数率(U1、U2、U3和U4)乘以仪器常数c后进行平均、滤波以及高分辨率处理后得到的高分辨率自然伽马测井曲线(GRH)与常规自然伽马测井记录(GR)的对比。不难看出,GRH与GR的一致性比较好,但GRH的分辨率更高,对薄层的响应更好。此外,图4c和d还给出了高分辨率声波时差(ACH)曲线以及微电极(RMN和RMG)和微球型聚焦(RMSFL)测井曲线的对比。结果清楚显示,在低阻泥岩薄层和高阻砂岩薄层上,GRH曲线均有较明显响应。
最后,图5给出另一口试验井不同处理方法所得自然伽马曲线的对比。其中,GR10FZJ表示利用本文提出的平均、滤波以及高分辨率处理技术得到的结果;GR是常规自然伽马曲线;RMG和RMN是微电极电阻率测井曲线;RMSFL为微球型聚焦电阻率测井曲线。从该图可以看出,由平均、滤波以及高分辨率处理技术得到的测井曲线GR10FZJ具有较高的纵向分辨率。
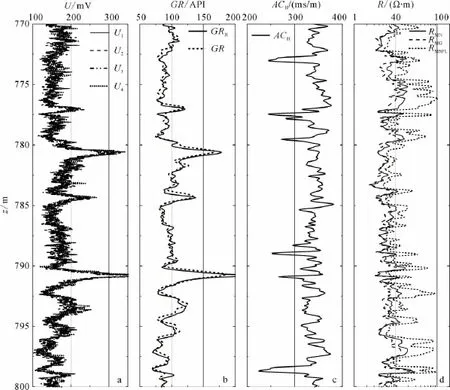
图4 井场试验资料处理结果Fig.4 Process results of field logs
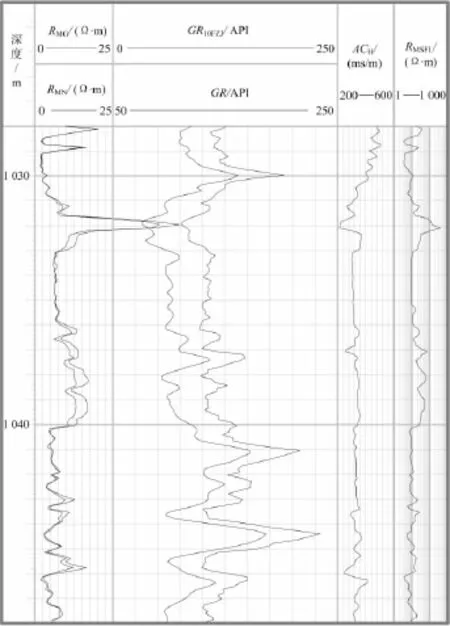
图5 不同处理结果的对比Fig.5 Comparison of results by different methods
4 结论
通过对不同晶体长度的自然伽马探测器响应函数特征的对比和考察,证实了通过减小探测器晶体长度能够有效提高自然伽马仪器的纵向分辨率;然而,晶体长度较短的探测器将减少探测器在单位时间内接收到伽马粒子数,从而会降低仪器探测精度。为此,采用4个完全相同的探测器同时测量伽马射线,并通过对4个测量值的平均、带限滤波以及正则化反褶积等方法,能够有效降低测量结果中统计涨落效应,并获得纵向分辨率达到0.15m高分辨率自然伽马测井记录。理论模型和井场试验结果均证明新的自然伽马测井仪器具有更高的纵向分辨率。
(References):
[1] Sheng P,White B,Nair B,et al.Bayesian Deconvolution of Gamma-Ray Logs[J].Geophysics,1987,52(11):1535-1546.
[2] Gadeken L L,Merchant A G,Jacobson A L,et al. The Utility of co mbining Smoothing and Deconvolution in Processing algorithm for Well Log Data[J].Proceedings of IEEE Nuclear Science,1990:810-816.
[3] 汪宏年,李舟波,常明澈,等.提高自然伽马测井曲线分辨率的正则化方法[J].地球物理学报,1997,40(6):847-856.
Wang Hong-nian,Li Zhou-bo,Chang Ming-che,et al.Regularized Algorithm for Enhancement of Vertical Resolution of Natural Gamma-Ray Log[J].Chinese Journal of Geophysics,1997,40(6):847-856.
[4] 汪宏年,李舟波,常明澈.地球物理测井综合高分辨率处理系统及其应用[J].测井技术,1996,20(6):441-448.
Wang Hong-nian,Li Zhou-bo,Chang Ming-che.The Integrated Processing System to Enhance Vertical Resolution of Geophysical Well Logs and Its Application[J].Well Logging Technology,1996,20(6):441-448.
[5] 李舟波.钻井地球物理勘探[M].北京:地质出版社,1995.
Li Zhou-bo.Geophysical Prospecting in Borehole[M].Beijing:Geological Publishing House,1995.
[6] 姚东华,汪宏年,陶宏根,等.水平层状介质中双侧向测井资料的正则化迭代反演与后验正则化因子选取[J].地球物理学报,2010,53(10):2227-2236.
Yao Dong-hua,Wang Hong-nian,Tao Hong-gen,et al.Iterative Tikhonov Regularization Inversion for Dual Laterolog in Horizontally Stratified Media[J].Chinese Journal of Geophysics,2010,53(10):2227-2236.
[7] 汪宏年,陶宏根,王桂萍,等.双感应测井资料的快速近似迭代反演[J].地球物理学报,2007,50(5),1614-1622.
Wang Hong-nian,Tao Hong-gen,Wang Gui-ping,et al.A Fast Approximate Iterative Inversion Technique of Dual Induction Logging Data[J].Chinese Journal of Geophysics,2007,50(5):1614-1622.
[8] 陶宏根,李庆锋,王桂萍,等.双感应测井资料实用化快速迭代反演技术及其在大庆油田的应用[J].测井技术,2007,31(5):441-445.
Tao Hong-gen,Li Qing-feng,Wang Gui-ping,et al.A Practical Fast Iterative Inversion Technique of Dual Induction Logging Data and Its Application in Daqing Oilfield[J].Well Logging Technology,2007,31(5):441-445.
[9] Wang Hong-nian.Simultaneous Reconstruction of Geometric Parameter and Resistivity Around Borehole inHorizontally Stratified Formations from Multiarray Induction Logging Data[J].Proceedings of IEEE Transactions on Geosciences and Remote Sensing,2003,41(1):81-89.
[10] 王斌,范晓敏.围岩对自然伽马测井响应的数值模拟[J].吉林大学学报:地球科学版,2006,36(增刊):166-168.
Wang Bin,Fan Xiao-min.Application of Numerical Simulation in the Rocks Influences the Gamma-Ray Logging[J].Joural of Jilin University:Earth Science Edition,2006,36(Sup.):166-168.
Optimizing Design of New High Resolution Gamma Ray Logging Device and Data Processing Technique
Tao Hong-gen1,2,Shang Qing-long3,Liu Chang-wei2,WANG Hong-nian3,Li Zhou-bo1
1.College of GeoExploration Science &Technology,Jilin University,Changchun 130026,China 2.Wireline Logging Company,Daqing Drilling Engineering Company,Daqing 163412,Heilongjiang,China 3.College of Physics,Jilin University,Changchun 130012,China
By studying the relation between response characters and the lengths of Gamma ray detector,we choose 0.1mlength of NaI scintillation detectors to develop a new high resolution Gamma ray tool which measures the total Gamma ray flux emanating from the formation.To overcome the increase of statistical fluctuation errors arising from the reduction of Gamma ray count rates due to the short detector,we assemble four detectors of the same type to achieve the four logs of Gamma ray fluxes with high vertical resolution simultaneously.And we sum up the four different curves from the detectors and then execute low-pass filter to reduce statistical fluctuation error in the Gamma ray logs.After that,we apply regularized deconvolution to enhance the vertical resolution of Gamma ray logs.The theoretical modeling and field results prove that the new Gamma ray tool has the vertical resolution up to 0.15m,whose vertical resolution is about 4times higher than that of other conventional Gamma ray tools.
book=2012,ebook=550
P631.81
A
1671-5888(2012) 04-0906-08
2011-11-03
国家自然科学基金项目(40874058)
陶宏根(1963-),男,博士研究生,教授级高级工程师,主要从事资料处理和解释方面的研究,E-mail:taohg@cnpc.com.cn
汪宏年(1962-),男,教授,博士生导师,主要从事非均质与各向异性介质电磁场数值模拟与反演研究,E-mail:wanghn@jlu.edu.cn。

