海洋运动对大尺度风场响应的解析研究*
赵艳玲,邓 冰,张 铭,刘天军
(1.中国人民解放军61741部队,北京100094;2.北京应用气象研究所,北京100029;3.中国人民解放军理工大学气象学院 大气环流与短期气候预测实验室,江苏 南京,211101)
海洋运动对大尺度风场响应的解析研究*
赵艳玲1,3,邓 冰2,3,张 铭3,刘天军2
(1.中国人民解放军61741部队,北京100094;2.北京应用气象研究所,北京100029;3.中国人民解放军理工大学气象学院 大气环流与短期气候预测实验室,江苏 南京,211101)
为探讨海洋向大尺度风应力响应的具体过程,建立了考虑海面风应力强迫的正压原始方程海洋模型,并利用Green函数做了解析求解和讨论。发现风应力引起的Ekman抽吸正比于风应力旋度。得到了海洋向风应力响应的具体形式:即海洋流场和压力场进行着准平衡的演变,并有海洋中压力梯度与科氏力之间的准地转平衡以及海洋Ekman体积输送的散度场与风应力旋度场之间的准平衡;此时有短周期的重力惯性波被激发,该波会较快弥散掉;而准平衡的演变则始终持续着。海洋在大尺度风场的强迫下的运动由重力惯性波、强迫惯性振荡和缓慢演变的准平衡过程三部分组成;前两部分是快过程,第一部分更快,第三部分是慢过程。最终海洋运动表现为强迫惯性振荡和准平衡演变过程的叠加。
大尺度风场;海洋模型;响应;Ekman抽吸
风应力驱动上层海洋的理论早在20世纪50年代就已出现[1],至90年代以来,海洋运动向风场的响应问题受到越来越多的关注。这种响应是海气相互作用的重要组成部分,在全球气候变化中起到了重要作用。直到目前,这方面的研究仍受到广泛重视。钱永甫等[2]利用POM模式(分辨率0.5°)研究了南海海流对冬季风应力的响应特征,认为南海浅表层海流和全流对定常风应力的响应时间均为120d,深层海流的响应时间较长。蔡树群等[3]利用一个分区性的正压、斜压衔接模式,考察了南海上层环流对季风转变的响应,发现在不同方式变化的季风转变、季风过渡时期,南海流场的调整有较大的差别,但在过渡之后最终的流场结构基本一致。对于渤、黄东海区域海流对冬季风应力的响应研究,赵保仁[4]利用黄海和东海近岸3个测站的观测资料作了初步探讨,认为上表层有离岸的Ekman输送时,趋岸的补偿流大约从1/3水深处直到海底的较厚水层中向岸流去,表层流大约6~12h可建立与风相适应的风生流动,底层流的适应时间大约是15~20 h。Qiu[5]则研究了东太平洋风应力强迫的Rossby波。Cabanes等[6]研究了风应力驱动的正压Sverdrup平衡和一阶斜压Rossby波。Qiu和Chen[7]还研究了南太平洋海表面高度时空变化的动力机制等。以上这些研究以诊断分析和数值模拟居多。在解析研究方面,Gill在文献[1]中指出,在一定条件下,此时海洋运动可分解为两部分:一部分是风应力作为直接强迫项驱动的强迫惯性振荡,在该部分压力梯度不起作用;另一部分是风应力引起的Ekman抽吸,此时则存在该抽吸引起的垂直运动,并通过其进一步影响海洋运动,该部分有压力梯度。然而总的看来,这方面的研究尚不很多。本研究曾建立了一个水平二维正压准平衡海洋模型,并在考虑西海岸的情况下,对气候尺度的准定常和时变风场(异常)强迫下的海洋流场响应做了解析求解[8],并试图解释中纬度北太平洋实际流场异常的原因。因该模型做了准平衡(准无辐散)近似,重力惯性波被滤去了,故其仅能反映海洋对大尺度风应力响应的最终状态,而不能给出其响应的具体过程,这点为其局限所在。为此,本研究建立了一个考虑海面风应力强迫的线性化正压原始方程海洋模型,在对该模型做了理论分析后,进一步对该模型做了解析求解和讨论,以便探讨正压海洋对大尺度风应力响应的具体过程。
1 数学模型
海洋对风应力的线性化正压响应方程组[1]为:

式中,u为x方向流速,v为y方向流速;Xs,Xb分别表示海面风应力和海底摩擦应力的x方向分量,Ys,Yb则为y方向分量;η为受扰后流体厚度与未受扰流体厚度的偏差,H为未受扰流体厚度,ρ为流体密度,两者均取为常数。令

式中,UE,VE是海面与海底边界层的Ekman体积输送,其满足方程

而up,vp则满足以下方程

在此φ=gη,其为位势偏差。在式(4)中,强迫项已被消去。将式(2)代入式(1)的连续方程中,再乘以g,则可得

这里co2=gH,wE=∂UE/∂x+∂VE/∂y,其为由风应力造成的Ekman抽吸的垂直运动。当海洋表面出现体积辐散时,其下部的水要向上涌升,故有wE>0,反之亦然。
由此可见,风应力造成的海洋运动能够分解成两部分。一部分是风应力作为直接强迫项驱动的强迫惯性振荡,其控制方程组由式(3)式决定,注意在该部分压力梯度不起作用。另一部分是风应力引起的Ekman抽吸,此时存在Ekman抽吸引起的垂直运动,并通过该垂直运动进一步影响海洋运动;其控制方程为式(4)和式(5),该部分有压力梯度。
对于第一部分即海洋的强迫惯性振荡部分,文献[1]已给出了直角坐标系下的解,还讨论了在极坐标下热带气旋造成的海洋强迫振荡问题[9],故本研究就不再讨论该问题了。下面重点对第二部分进行讨论。在讨论之前,先来估计wE与风应力(Xs,Ys)之间的关系。
若不考虑海底摩擦应力,由式(3)可得,

将以上UE、VE代入wE=∂UE/∂x+∂VE/∂y式中,则有,

若假定海洋运动呈准定常或相对惯性时间尺度f-1变化很缓慢,即其属海洋大尺度运动,此时在热带外海洋其运动的时间尺度大于1d,空间尺度大于100km(气候问题中海洋运动显然属该大尺度范畴);本文章中的“海洋”均为以上所指的大尺度海洋,在此不讨论海洋中小尺度的问题,以下不再赘述。这样式(7)最后1个等号右边的第二项相对于第一项是小项,其可略,故此时有:

即Ekman抽吸正比于风应力的旋度,且此时有海洋Ekman体积输送的散度场和风应力旋度场之间的准平衡,并能得到Ekman抽吸的估计式(8),用该式则可从风应力的分布诊断得到Ekman抽吸的垂直运动。
2 方程的求解
现设海洋运动属海洋大尺度,此时方程(5)可写为:

式中,aφ=∂YS/∂x-∂XS/∂y为风应力的旋度。方程组(4)和(9)构成了上述海洋运动第二部分的控制方程组。下面对该方程组进行求解。
首先用式(4)可分别求得涡度方程和散度方程:
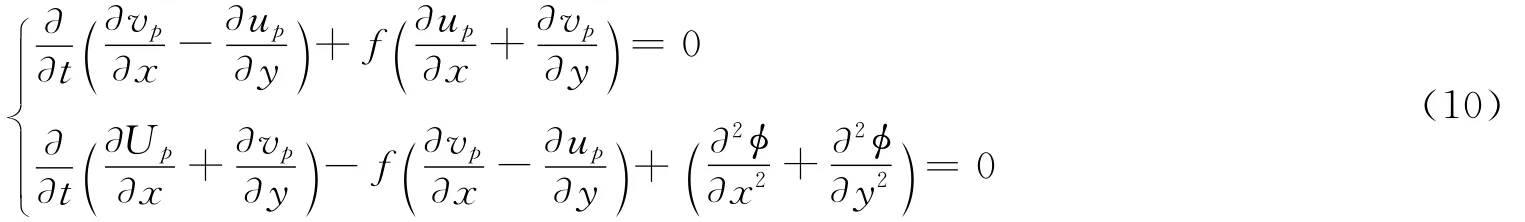
然后消去涡度,可得,

这里算子Δ=∂2/∂x2+∂2/∂y2,为二维Laplace算子。最后将式(9)与式(11)联立以消去散度,则可得一个与单一变量φ的倾向即∂φ/∂t有关的方程:



在此算子

其为正压流体的波动算子,而BΩ,Bφ,Bu,Bv则定义如下:

由上式可见,BΩ,Bφ,Bu,Bv则均与风应力的旋度有关。
对于全平面的情况,非齐次方程的解可由相应齐次方程的解加上非齐次项导致的“推迟位势”来表示。对式(13)~(15)来说,齐次方程组Λ(F)=0是典型的波动方程(F 为∂up/∂t,∂vp/∂t,∂φ/∂t),存在有满足初值F(x,y,0)=F(0)(x,y)和∂F(x,y,0)/∂t=F(1)(x,y)的唯一解;这样对非齐次方程组Λ(F)=-A(x,y,t)而言(这里-A为非齐次项,即式(13)~(15)中等号右端的部分,其均与风应力的旋度有关),则借鉴文献[10]中的数学处理,可得到其解为:

其中

在此有

而在式(18)~(20)中r的表达式则为

注意,式(18)中的F 实为倾向,即∂φ/∂t、∂up/∂t和∂vp/∂t。将式(18)对时间t积分,此时要用到分部积分和积分号下求微商等运算,最终可得[10]:


其中,

这样就求出了非齐次方程组式(13)~(15)的解,该解也是控制方程组式(4)和(9)的解。以下将对该解做出分析讨论。
3 讨 论
以下仍然借鉴文献[10]中的思路来进行分析讨论。当存在风应力的外强迫,即Aφ≡0时,则由解式(22)~(24)可见,其可分为两部分(该两部分在式(22)~(24)中分别用大括号括起)。第一部分(下标为I的部分)为初始场的影响,其中包括初始风应力场的影响,但初始风应力场只直接影响φ(x,y,t),而不直接影响up(x,y,t),vp(x,y,t)(因这两者无A(0)φ项)。第二部分则为外强迫,即风应力强迫对解的影响,并给出了大尺度海洋向风应力响应的具体形式。
以上已指出,第一部分为受初始扰动影响的φi,upI,vpI,注意到,若初始扰动只局限在局部地区,或有(∂φ/∂t)(0),(∂up/∂t)(0),(∂vp/∂t)(0)以及等均 ∈L2,即在全平面能量有限,则在较长时间后,因重力惯性波的弥散,φI,upI,vpI将趋于平衡。这种平衡是海洋中压力梯度与科氏力之间的地转平衡。若(∂φ/∂t)(0)等不局限在有限地区,但设初始时刻扰动是准地转的(这表明初始风应力引起的海洋非地转运动不明显),则在任何时刻φI,upI,vpI始终是准地转的。
以下分析第二部分。这部分决定外强迫即风应力对海洋适应过程的影响(如果有适应过程的话,由下文可见,对大尺度风应力的确有适应过程)。从式(22)~(24)可见,BΩ,Bφ,Bu,Bv描述了风应力激发出的海洋扰动,其与 Green函数0(r,t-t′)和∂0(r,t-t′)/∂t′密切有关。这两种 Green函数的图形如图1、图2所示。图1给出了Green函数随时间的变化,其横坐标是无量纲时间τ=f·t,其中f为地转参数,t为时间,纵坐标则是与Green函数0和∂0/∂t′有关的各种函数值κ(其中也包含这两种Green函数的值),值κ也均为无量纲量,而各种函数的具体形式则见图1右方数字1~5后的表达式。图2给出了Green函数0(r,t-t′)/∂t′和∂0(r,t-t′)的空间分布,其横坐标为无量纲距离ξ=fr/c0→0)。由图1可见,当t→∞即τ=f·t→∞时则有~K0(r,t)→(fr/c0)(由该图可见曲线2逼近直线3,在此K0是虚变量零阶Bessel函数),即麦克唐纳函数)0(r,t)围绕着平衡位置K0(fr/c0)上下摆动(参见该图上的曲线2);但当r很小时,即r<<c0/f,也即r远小于海洋运动的Rossby变形半径c0/f时,则0(r,t)恒为正;当r较大时(fr/c0>1),因K0(fr/c0)很小,0(r,t)才有可能为负,不过振幅很小。这说明在任一点上,其周围不远地区的BΩ的贡献是随时间和随地区积累的。若再设强迫海洋的风是准定常的或相对惯性时间尺度f-1变化得很缓慢(此时其属大尺度大气运动,即其时间尺度大于1d,空间尺度T大于1d,空间k度大于2 000km,注意大尺度大气的空间尺度典型值要远大于大尺度海洋),此时式(22)~(24)中第二个大括号中由BΩ所决定的这部分(该大括号中的第一项)就沿着比较确定的方向缓慢地演变着,呈现准平衡的状态,即是海洋中压力梯度与科氏力之间的准地转平衡以及海洋Ekman体积输送的散度场和风应力旋度场之间的准平衡。再注意到,∂0(r,t-t′)/∂t′围绕着0上下摆动(参见图1上曲线4),周期约略等于惯性振动周期2π/f。这说明,各点周围地区Bφ,Bu,Bu的贡献在时间上和空间上是相互抵消的,由此可知,式(22)~(24)中第二个大括号中的这部分(该大括号中的第二项)大体是沿时间振动着的,而且周期短,其具有重力惯性波的特点。总之,外源强迫即大尺度风应力的作用是使流场和压力场沿着某一方向进行着上述准平衡的演变,但同时又激发出环绕着该基本方向的短周期重力惯性波。

图1 Green函数随时间的变化Fig.1 Variations of the Green function with time

图2 Green函数的分布Fig.2 Distribution of the Green function
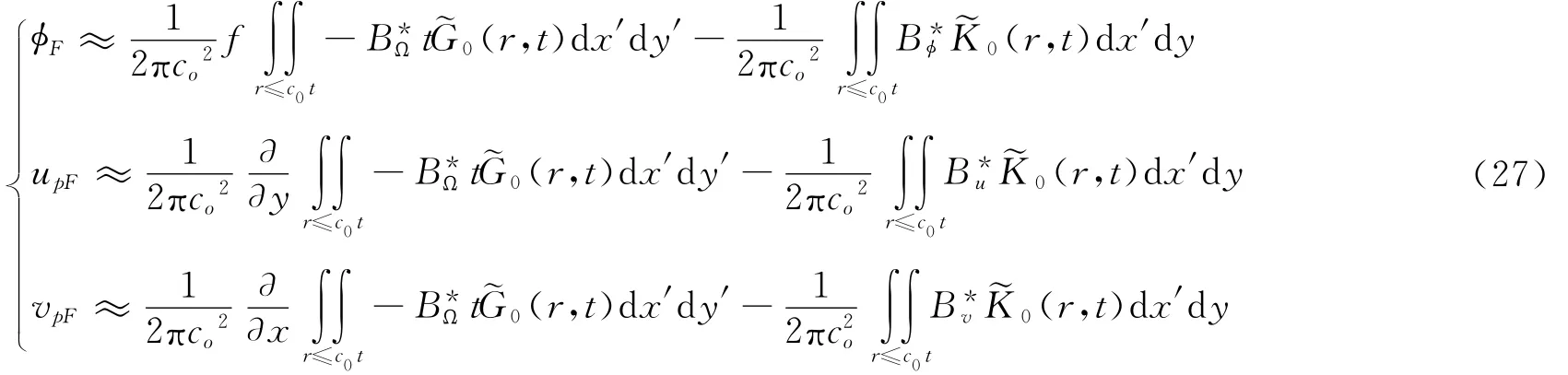
其中,


注意到影响最大的是r=0附近的扰源,于是根据式(29)可知,若满足以下的条件:的量级不小于的量级,∂/∂y的量级不小于f的量级,∂/∂x的量级不小于f的量级,则在t>>f-1之后,从整体来说,在式(27)的两项中以第一项占优,这种情况下外强迫即风应力所导致海洋响应的总效果是比较缓慢的演变。此时海洋运动以准平衡状态占优。流场的重力惯性波部分(式(27)中的第二项)相对于流场的准平衡部分(式(27)中的第一项)而言,其处于次要的地位。考虑到该风应力激发出的重力惯性波还会向全平面弥散,而使其振幅衰减,且准平衡的运动长期保留,并随时间缓慢演变,这样海洋在该风应力强迫下的这部分运动就可分为“快过程”即重力惯性波和“慢过程”即准平衡的演变过程两部分。该风应力不断激发出重力惯性波,同时使海洋沿着比较确定的方向比较缓慢地准平衡演变,且激发出的重力惯性波会弥散掉,而准平衡的演变则持续着。这就是海洋向该风应力的适应以及其演变的情况。
以上假设了风是准定常的或相对惯性时间尺度f-1变化很缓慢的(其属大气大尺度运动),而这种情况就是大尺度风场强迫海洋的情况。在考虑到式(17)并注意到有后,则此时有

式中,τ为大尺度大气运动的时间尺度,即平流时间尺度(τ大于1d),并有τ>f-1,在此f-1是惯性振动的时间尺度。此时有,

注意到τ>f-1则有

同样,

这里L为大气大尺度运动的空间尺度(L>2 000km)。此时,

故有,

同理有,

4 结 语
本研究建立了一个考虑海面风应力强迫的正压原始方程海洋模型,以探讨海洋向风应力响应的具体过程。将海洋运动对风场的响应分解成相对独立的两部分:第一部分是风应力作为直接强迫项驱动的强迫惯性振荡,在该部分压力梯度不起作用;第二部分是风应力引起的Ekman抽吸,此时则有该抽吸引起的垂直运动,并通过其进一步影响海洋运动,该部分有压力梯度。因第一部分已有研究,故本文章只讨论第二部分,并仅对大尺度风场强迫海洋运动的情况做了解析研究。首先对风应力引起的Ekman抽吸做了估计,得到在大尺度海洋Ekman抽吸正比于风应力旋度的结论。然后通过对该抽吸引起的该海洋模型控制方程组的求解,给出了海洋向大尺度风场风应力响应的具体形式:其是使流场和压力场沿着某一方向进行准平衡的演变,并有海洋中压力梯度与科氏力之间的准地转平衡和海洋Ekman体积输送的散度场与风应力旋度场之间的准平衡。与此同时,有短周期的重力惯性波被激发出来。该重力惯性波会较快弥散掉,而准平衡的演变则始终持续着。故海洋在大尺度风场的强迫下其运动由以下三部分组成:第一部分是强迫惯性振荡,其时间尺度是f-1,这是1个快过程;第二部分是比较缓慢演变着的准平衡过程;第三部分是重力惯性波,这也是快过程,其时间尺度比惯性振荡还要短。第二部分与第三部分相比,前者占优且后者还要向全平面弥散,故最终海洋运动表现为强迫惯性振荡和准平衡演变过程。
最后要指出的是,本研究只讨论了海洋运动对大尺度风场的响应,对于海洋运动对中小尺度风场的响应,则在文献[9]中做了介绍。
参考文献(References):
[1] GILL A E.Atmosphere-ocean dynamics[M].Translating by ZHANG L Z,LE K T,ZHAO X Y.Beijing:Ocean press,1988.GILL A E.大气-海洋动力学[M].张立政,乐肯堂,赵徐懿,译.北京:海洋出版社,1988.
[2] QIAN Y F,WANG Q Q,ZHU B C.Responsive properties of oceanic currents in the south china sea to wind stress of winter monsoon[J].Scientia Meteorologica Sinica.2000,20(1):1-8.钱永甫,王谦谦,朱伯承.南海海流对冬季风风应力的响应特征[J].气象科学,2000,20(1):1-8.
[3] CAI S Q,SU J L,GAN Z J.Response of south china sea upper circulation to monsoon transition[J].Journal of Troical Oceanography.2001,20(1):52-60.蔡树群,苏纪兰,甘子钧.南海上层环流对季风转变的响应[J].热带海洋学报,2001,20(1):52-60.
[4] ZHAO B R.A study of the effects of local wind on currents in the off-shore areas of the east china sea and huanghai sea[J].Chinese Journal of Oceanology and Limnology,1982,13(6):479-490.赵保仁.局地风对黄海和东海近岸浅海海流影响的研究[J].海洋与湖沼,1982,13(6):479-490.
[5] QIU B.Kuroshio Extension variability and forcing of the Pacific decadal oscillations:responses and potential feedback[J].J.Phys.Oceanogr.,2003,33:2465-2482.
[6] CABANES C,HUCK T,VERDEREE C D.Contributions of wind forcing and surface heating to interannual sea level variations in the Atlantic Ocean[J].J.Phys.Oceanogr.,2006,36:1739-1750.
[7] QIU B,CHEN S.Decadal variability in the large-scale sea surface height field of the South Pacific Ocean:Observations and causes[J].J.Phys.Oceanogr.,2006,36:1751-1762.
[8] ZHANG Y C,LU K C,ZHANG M.Barotropic quasi-equilibrium ocean model and its solution.PartⅠ:Mid-latitude forcing of large-scale wind field[J].Journal of the Meteorological Sciences Scientia Meteorologica Sinica,2011,31(1):11-16.张永垂,路凯程,张铭.正压准平衡海洋模型及其解Ⅰ-中纬度大尺度风场强迫情况[J].气象科学,2011,31(1):11-16.
[9] ZHAO Y L.Analytical study on response of ocean to wind stress and high resolution numerical research on sea wave and current in the Bohai Sea,the Yellow Sea and the East China Sea[D].Nanjing:Doctor degree thesis of PLA univ.of sci.and eng.,2008.5.赵艳玲.海洋对风应力响应的解析研究及渤黄东海浪流的高分辨率数值研究[D].南京:中国人民解放军理工大学,2008.
[10] ZENG Q C.Numerical physical basis of numerical weather prediction I[M].Beijing:Science press,1979.曾庆存.数值天气预报的数值物理基础(第一卷)[M].北京:科学出版社,1979.
(杜素兰 编辑)
Analytic Research on the Response of Ocean Movement to Large-scale Wind Field
ZHAO Yan-ling1,3,DENG Bing2,3,ZHANG Ming3,LIU Tian-jun2
(1.Unit 61741,P.L.A,Beijing 100094;2.Beijing Institute of Applied Meteorology,Beijing 100029;3.Laboratory of Atmospheric Circulation and Short-range Climate Forecast,Meteorological College,P.L.A.University of Science and Technology,Nanjing 211101)
A barotropic primitive ocean model forced by the sea surface wind stress is established for discussing the response processes of the ocean to the large-scale wind stress,and the Green function is used to solve the analytic solutions of the ocean equations.It has been found that the strength of the Ekman pumping induced by wind stress is positively proportional to the curl of wind stress,and that the response form of the ocean to the wind stress can be described as a quasi-equilibrium evolution between the flow field and the pressure field in the ocean,which includes the quasi-geostrophic equilibrium between the pressure gradient in the ocean and the Coriolis force and the quasi-equilibrium between the divergence of Ekman transportation and the wind stress curl.Meanwhile,inertia gravity waves with short period will be excited out,but disperse very soon.However,the quasi-equilibrium evolution is always sustained.The ocean movement forced by large-scale wind field consists of the following three parts:the inertia gravity waves,the forced inertial oscillation and the quasi-equilibrium evolution.The first two parts are quick processes,with the first one being quicker than the second,and the third one is a slow process.The final performance of the ocean movement is the superimpostion of the forced inertial oscillation and the quasi-equilibrium evolution.
large-scale wind field;ocean model;response;Ekman pumping
October 11,2011
P732
A
1671-6647(2012)03-0328-10
2011-10-11
国家重点基础研究发展规划项目——北太平洋副热带环流变异对大气强迫的反馈作用(2007CB411805)
赵艳玲(1980-),女 ,河北唐山人,工程师,博士,主要从事物理海洋方面研究.E-mail:bbygg99@yahoo.com.cn

