双组元离心式喷注器雾化性能的大涡模拟数值研究
汪凤山,毛晓芳,虞育松,张 榛,王 平
(1.北京控制工程研究所,北京100190;2.北京交通大学,北京100044)
双组元离心式喷注器雾化性能的大涡模拟数值研究
汪凤山1,毛晓芳1,虞育松2,张 榛1,王 平1
(1.北京控制工程研究所,北京100190;2.北京交通大学,北京100044)
基于气液两相体积混合分数建立某型双组元离心式喷注器内部流场及雾化场的数学模型,并采用大涡模拟(LES)方法对其雾化性能进行研究.计算结果表明,喷注器外路喷射速度低于内路喷射速度,内外两路同时喷射时,两路相互影响,雾化锥角增加;随着喷注器出口直段长度的增加,内外路喷射速度和流量系数均呈单调下降趋势;随着喷注压降的增加,喷注器流量系数和出口喷射速度随之增加,而雾化粒度不断降低,雾化锥角不断增大.
同轴离心式喷注器;混合分数模型;大涡模拟;数值模拟;雾化粒度;雾化锥角
随着航天科技的发展,新一代大型、长寿命卫星对双组元姿控发动机的稳态及脉冲工作性能要求提出了更高的要求.液体火箭发动机工作过程涉及到流动、雾化、燃烧及传热等多个过程,其中推进剂雾化是直接影响推力器比冲、可靠性与寿命的关键过程.为提高发动机的工作性能,通常需要对推进剂雾化单元(即喷注器)进行良好设计,尤其要对推进剂的雾化性能进行详细的研究.
液体雾化现象包括液膜形成、液膜破碎和雾滴形成,是一种复杂的物理过程,工质物性、喷注器结构设计、出口背压条件及入口压力等均对其雾化性能产生影响.一直以来,国内外学者试图通过采用流体力学原理建立对雾化过程的数学描述,并建立多种数学模型[1].目前,针对液体在入口压力作用下的雾化现象,通常采用欧拉近似方法与欧拉—拉格朗日迭代方法(即ALE方法)两种方数值方法进行仿真分析.第一种方法完全忽略喷雾粒子的初速和在流场中的受力,液滴分布完全由气流决定,通过平均计算,以拟流体的方法计算喷雾过程中的气流和喷雾粒子的运动规律.该方法的优点是计算工作量较小,速度快,能够在较短的时间内获得喷雾粒子的运动规律,特别适用于计算粒径较小、初速较低的喷雾输运现象,如饱和蒸气运动、煤粉输运过程等.第二种方法中喷雾粒子的运动不仅与初速有关,而且还受气动力的影响,运动规律通过拉格朗日方法进行描述,更符合喷雾过程的实际情况,能够捕捉到雾化过程中的一些细节现象,精度也较高,因此在实际中也应用较广.
针对双组元液体火箭发动机,喷注器出口推进剂雾滴速度通常较高,且在气流中的受力情况复杂,因此,不宜采用欧拉近似方法对其雾化过程进行仿真计算,通常采用欧拉-拉格朗日迭代方法.但由于喷雾粒子尺寸较小,受气流场中湍流运动关系密切,而通常采用的雷诺应力湍流模型空间分辨率较低,很难得到喷雾场的具体细节.如20世纪90年代,Jeng等[2-4]运用欧拉-拉格朗日迭代方法追踪压力旋流喷嘴的气液分界面,同时运用数值模拟和实验相结合的方法研究了结构参数对液膜厚度和喷雾锥角的影响.周立新等[5]采用基于单流体模型及气液两相混合分数概念对离心式喷嘴内部流场进行数值计算,并与Jeng的ALE方法进行对比.但由于采用了雷诺应力湍流模型,未能给出喷雾场的具体分布规律.
大涡模拟(LES)方法是通过将耗散尺度的湍流脉动过滤掉,只求解大尺度湍流脉动的一种新型纳维-斯托克斯(N-S)方程数值求解方法.与传统的雷诺时均模型(RANS)方法相比,具有分辨率高、普适性高、更能真实反映流动微观结构等优点,但计算量要比雷诺时均模型方法的要大.该方法能够得到较为精细和准确的流场细节,为通过采用数值计算的方法获得喷雾场的细节提供了可能.随着近年来计算机运行速度和计算能力的迅速进步,采用大涡模拟方法已经可以处理部分工程问题的湍流流动,在国内外喷雾学界已经得到了越来越广泛的应用.
本文通过采用大涡模拟数值方法对某型双组元离心式喷注器的喷雾流场进行了数值仿真分析,得到了不同条件下喷注器的雾化性能参数和液滴分布特性,探索喷注器雾化特性数值求解的可行性与方法,所得结果可为未来双组元喷注器的设计提供参考.
1 数值仿真模型与算法
1.1 气液两相流数学模型
针对喷注器出口喷雾区域内同时存在气液两种不相容工质,气液两相之间存在界面的情况.为对气液两相共存情况进行描述,通过引入体积分数的概念,可实现采用一组纳维-斯托克斯(N-S)方程描述气液两相及相界面,这种方法被称之为体积分数法(VOF),单元体积分数εk的计算公式为
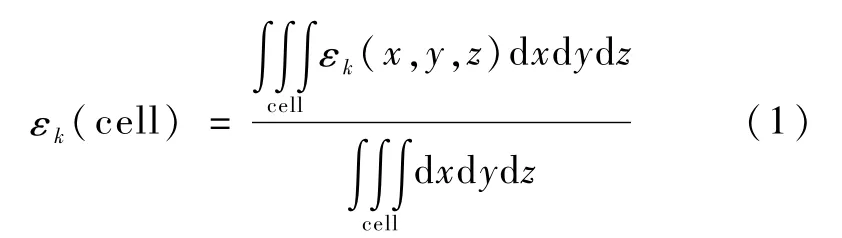
通过引入体积分数,对于液体喷雾特性可用如下基于压力、速度和体积分数的N-S方程描述:△
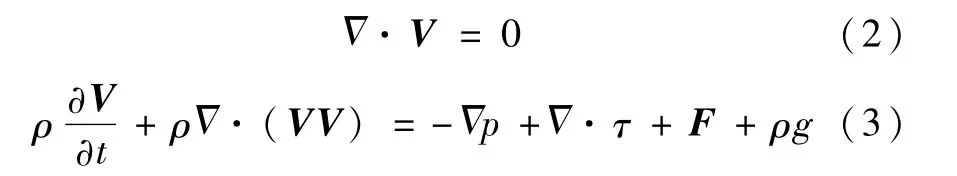
对于牛顿流体,在斯托克斯假设下:
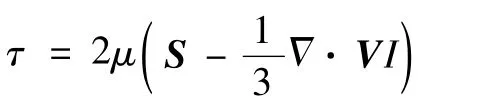
由公式可得:

式中,V为流体速度矢量,ρ为流体密度,p为流体各向同性压力,F为体积力(表面张力),g为重力,μ为流体动力黏度,τ为剪应力,I=δij为克罗内克符号,S为速度梯度张量.对于牛顿流体,粘性系数为常数,则:

考虑到:
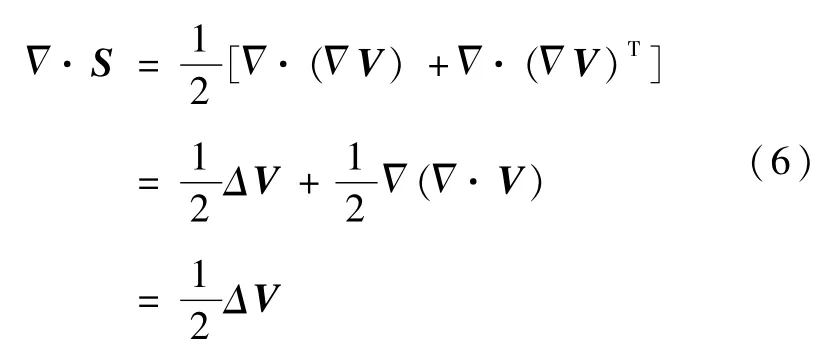
将方程(6)代入方程(5),则有:△

相界面的跟踪是不相溶多相流数值模拟的关键问题之一,通过基于异相流体混合分数的假设,VOF方法可以建立每一相流体体积分数的输运方程,对相界面进行跟踪:
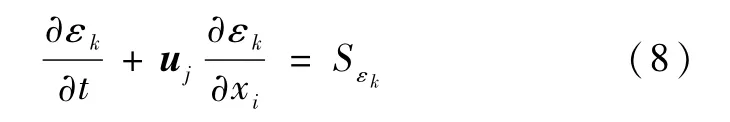
式中,Sεk是描述相间质量转移的物理量,由于雾化过程模拟不考虑相变,因此相间不存在质量转移,即Sεk=0.对于一定体积分数下的密度和黏度满足:
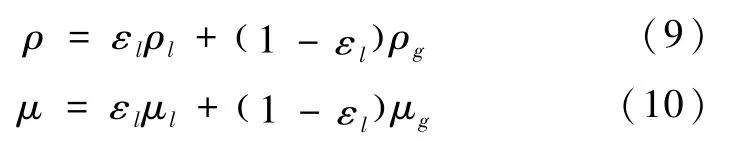
式中,下标l和g分别代表液相和气相.
气、液相界面结构在流场作用下变得非常复杂,精确求解三维空间的界面曲率和表面张力相当困难.Brackbill等[6]利用较为简洁的连续表面张力模型(CSF)解决了表面曲率和表面张力求解的问题,具体的表达式为:
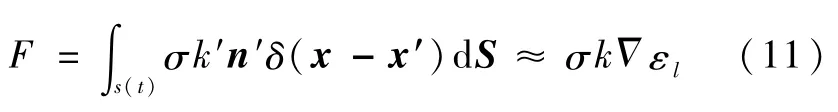
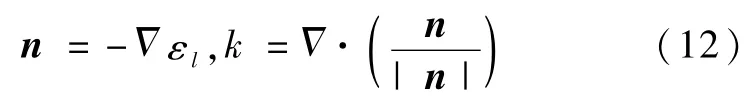
1.2 方程的数值解法
N-S方程的基本特点是非线性和耦合性,在一般情况下不能用解析方法得到封闭形式的解,因此需要采用一定的数值解法对N-S方法进行求解.在本文中,通过采用LES方法来完成对控制方程的数值求解.
LES方法求解N-S方程的思想是对控制方程进行滤波处理,将流场中的大小湍流涡团进行分离.大尺度湍流涡由控制方程直接求解;小尺度湍流涡通过引入亚网格尺度(SGS)湍流模型进行模拟求解.由于小尺度湍流涡结构比大尺度湍流涡具有更好的各向同性,因此LES对SGS模型的要求不像雷诺应力模型(RANS)那样高.当大涡模拟的网格间距逐渐减小时,SGS黏度趋于零,预测结果逐渐逼近直接数值模拟(DNS)结果.
在采用LES数值方法对N-S方程求解过程中,为了使方程封闭,需要引入模型对该亚网格尺度应力项进行计算.目前,使用最广泛且最简单的亚网格尺度应力模型是Smagorinsky涡黏性模型[7],该模型通过建立未知亚网格尺度应力与已知的变形速率张量之间的简单函数关系来实现对亚网格尺度应力项的模拟.假设亚网格应力张量正比于平均应力张量,则:
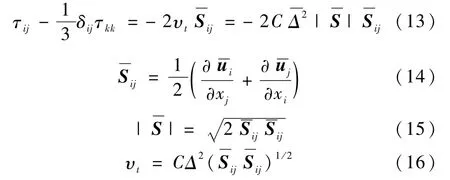
式中,δij为克罗内克符号,是已知的应变张量,υt为湍流涡黏度(m2/s),为滤波尺度(定义为(△χ△y△z)1/3).LES的湍流涡黏度υt∝uλ,其中,u
式中,k是表面曲率,σ是表面张力系数,n是垂直表面的法向单位向量,εl为液相体积分数,其中:是流动速度,λ为最大的耗散湍流涡泰勒尺度(Taylor尺度).
通过对上述微分方程组离散化,将连续变化形式描述的微分方程转化为离散形式的代数方程,采用有限体积法在计算机上进行数值求解.
2 仿真分析
2.1 喷注器的几何结构
本文研究的喷注器采用双旋涡离心喷嘴结构,该结构具有雾化效果好,喷雾场分布均匀,以及便于在燃烧室壁面组织液膜冷却等优点,如图1所示.为了尽量减小数值计算的网格数量,取网格平均间距为100μm,总网格单元数约5×106,喷嘴外区域的张角根据试算预先确定.
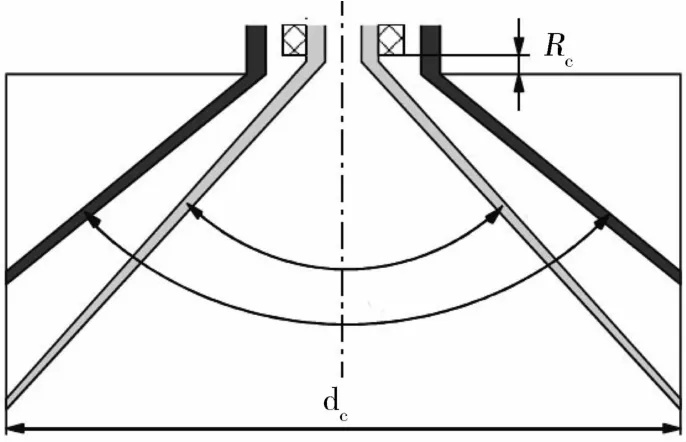
图1 双旋涡离心喷注器工作原理图Fig.1 Principle of coaxial centrifugal injector
2.2 边界条件
在喷注器入口处根据给定压力入口边界条件,湍动能和耗散率根据经验公式给出,出口设置压力出口边界条件,壁面设置无滑移固体边界条件,近壁函数采用标准壁面函数法求解.
3 仿真结果与分析
图2为喷注器在不同时刻的喷雾形态数值仿真结果,从图中可以看出,液体离开喷嘴后,液膜迅速分裂为数根细长的液丝,随后连续液丝会分裂为较长的离散液滴,从而完成整个雾化过程.对于外路喷嘴,由于出口液滴喷射速度相对较低(约4m/s),其雾化过程相对较慢;而对于内路喷嘴,由于出口液滴喷射速度较高(约9m/s),其雾化过程进度相对较快,但喷雾形态具有明显的周向不对称性,喷雾边缘区域存在较长的连续液丝;对于两路同时喷射的情况,内外喷嘴出口液滴相互之间发生强烈的相互作用,雾化速度介于内外路独立喷射之间,且基本消除了内路单独喷射时的周向不对称现象.

图2 喷注器不同时刻的喷雾形态Fig.2 Shape of the propellant spray varied with time
图3 为喷注器在不同时刻喷雾锥角变化示意图.从图中可以看出,对于喷注器,大概经过4ms左右,其喷雾锥已基本成形.由于外路速度较低,其雾化锥角与实际数值(110°)相差较大,而内路雾锥角度却略小于实际数值(90°);内外两路同时喷射时,由于同向旋流叠加的加强作用,其雾化角度比内外路单独喷射的时候均略有增加.
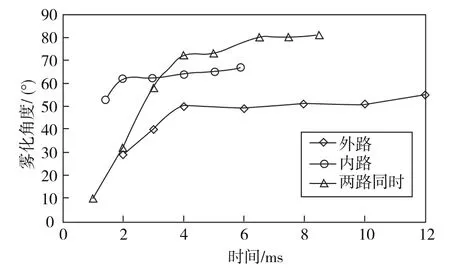
图3 喷注器雾化锥角随时间的变化Fig.3 Spray angle varied with time
图4 为在0.5MPa压差下,不同出口直段长度下喷注器喷射速度与流量系数的变化示意图.从图中可以看出,随着出口直段长度的增加,内外路喷射速度和流量系数均呈单调下降趋势.可见随着出口直段长度的增加,在摩擦力的作用下,喷注器总流阻不断增加,从而导致喷嘴旋流速度不断降低,进而影响到喷注器喷雾特性.
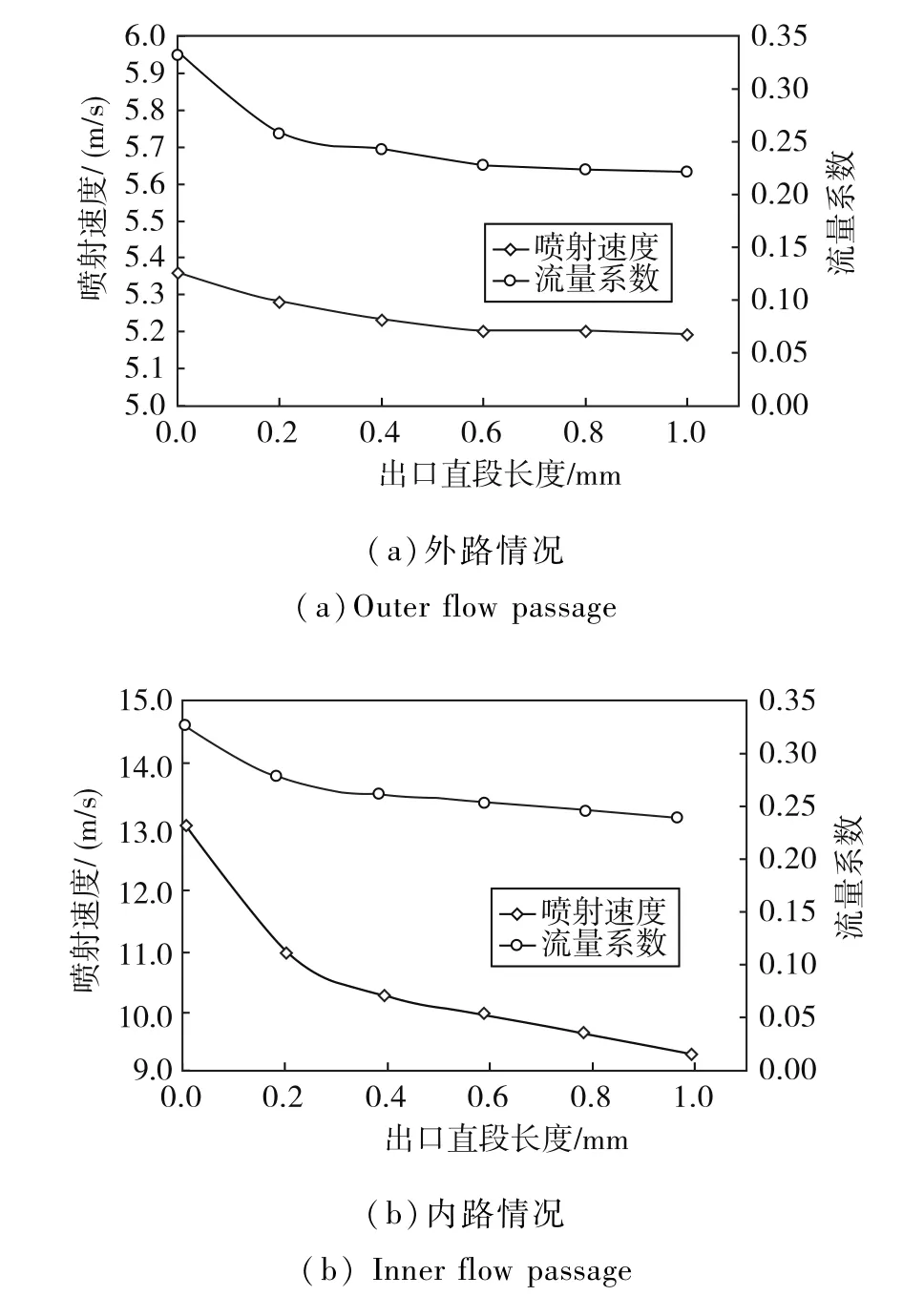
图4 内外路喷射速度和流量系数随出口直段长度的变化Fig.4 Spray velocity ejected from the flow passage varied with the injector exit length
图5 为不同喷注压差下内外路喷射速度和流量系数的变化.从图中可以看出,随着喷注压差的增大,喷注器喷射速度和流量系数也随之增大.
图6为外路喷嘴雾化粒度和雾化锥角随喷注压降的变化.从图中可以看出,随着喷注压降的增加,外路雾化粒度不断降低,雾化锥角不断增大.可见,随着喷注压降的提高,液体出口速度不断升高,液膜与气流之间的剪切作用更为强烈,液膜的不稳定性增强,雾化粒度不断降低;另外,由于喷注压降的升高,增强了出口液膜的旋流速度,从而导致形成的雾锥角增大.
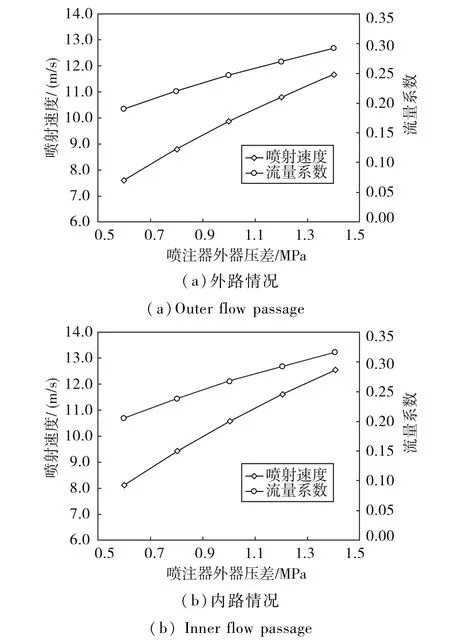
图5 内外路喷射速度和流量系数随喷注压差变化计算结果Fig.5 Spray velocity from the flow passage and flow coefficient varied with the injector pressure drop
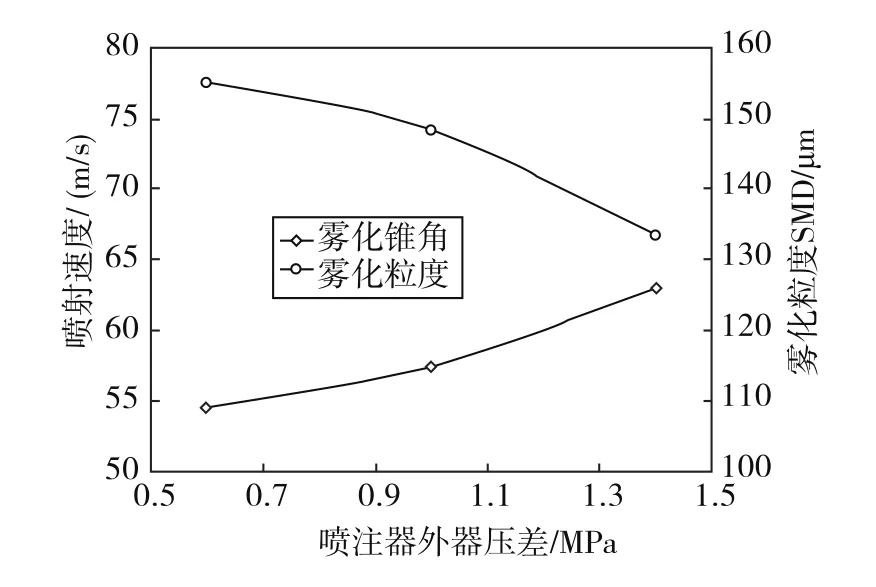
图6 外路雾化锥角和雾化粒度随喷注压差的变化Fig.6 Spray velocity and SMD ejected from the outer flow passage varied with the injector pressure drop
4 结 论
本文通过引入气液两相流体积分数近似方法描述气液两相及相界面特性,并采用LES方法对某型双组元离心喷注器的雾化性能进行了数值研究,结果如下:
1)喷注器外路喷射速度低于内路喷射速度,从而导致外路达到雾化稳定的时间要比内路更长;
2)内外两路同时喷射时,两路相互影响,由于旋转方向相同的缘故,喷注器雾化锥角较两路均有所增加;
3)随着喷注器出口直段长度的增加,内外路喷射速度和流量系数均呈单调下降趋势;
4)随着喷注压降的增加,喷注器流量系数和出口喷射速度随之增加,而雾化粒度不断降低,雾化锥角不断增大.
对计算结果进行分析,可见通过引入体积分数(VOF)对气、液两相雾化流动纳维-斯托克斯(N-S)方程进行简化,并采用大涡模拟(LES)的方法对其进行数值求解,能够较为准确地捕捉到雾化过程中的细节,计算精度也较高,是一种值得推广应用喷注器雾化过程数值仿真方法.如能通过与实验测试数据进行充分比较和分析,近一步优化计算模型,将能为液体火箭发动机喷注器的设计、优化提供更准确的参考依据.
[1] Lefebvre A H.Atomization and sprays[D].Hemisphere Publishing.New York.1989
[2] Jeng SM,Joe M A,et al.Computational and experimental study of liquid sheet emanating from simple fuel nozzle[R].AIAA-97-0796
[3] Holtzclaw D,Sakman T,Jeng SM,et al.Investigation of flow in a simplex fuel nozzle[R].AIAA-97-2970
[4] Rizk N K,Chin J S.Comprehensive fuel nozzle model [R].AIAA-94-3278
[5] 周立新,雷凡培.离心式喷嘴内流场特性的数值模拟[J].推进技术,2002,23(6):480-484 Zhou L X,Lei F P.Numerical simulation of internal flow field of swirl nozzle[J].Journal of Propulsion Technology,2002,23(6):480-484
[6] Brackbill J U,Kothe D B,Zemach C.A continuum method for modeling surface tension[J].Journal of Computational Physics,1992,100:335-354
[7] Smagorinsky J.General circulation experiments with the primitive equations.I.the basic experiment[J]. Monthly Weather Review,1963,91(3):99-164
Num erical LES Study of Sp ray Perform ance in a Bi-Propellant Coaxial Centrifugal In jector
WANG Fengshan1,MAO Xiaofang1,YU Yusong2,ZHANG Zhen1,WANG Ping1
(1.Beijing Institute of Control Engineering,Beijing 100190,China; (2.Beijing Jiaotong Uniυersity,Beijing 100044,China)
A numerical study of spray performance in a bi-propellant coaxial centrifugal injector is proposed by using the large eddy simulation(LES)method,based on themultiphase volume fraction model of the gas and liquid.The results show that the spray velocity ejected from the inner flow passage is larger than the outer flow passage,and the spray angle increases slightly when both of the two flow passages simultaneously inject.The spray velocity and flow coefficient increase with the decrease of the injector exit length and increase of the injector pressure drop.The spray droplet size(SMD)decreases and the spray angle increases with the increases of the injector pressure drop.
coaxial centrifugal injector;multiphase fraction model;large eddy simulation(LES);numerical study;spray droplet size;spray angle
V43
A
1674-1579(2012)06-0013-05
汪凤山(1981—),男,高级工程师,研究方向为双组元推力器技术;毛晓芳(1971—),女,研究员,研究方向为航天器推进技术;虞育松(1979—),男,副教授,研究方向为燃烧科学与技术;张 榛(1983—),男,工程师,研究方向为双组元推力器技术;王 平(1981—),男,高级工程师,研究方向为双组元推力器技术.
2011-08-10
DO I:10.3969/j.issn.1674-1579.2012.06.003

