一种基于固定配平的飞行器滚转制导律研究*
李自行,李高风,黄瑞玲
(1.北京控制与电子技术研究所,北京100038; 2.北京希曼顿自动化研究所,北京100080)
技术交流
一种基于固定配平的飞行器滚转制导律研究*
李自行1,李高风1,黄瑞玲2
(1.北京控制与电子技术研究所,北京100038; 2.北京希曼顿自动化研究所,北京100080)
具有固定配平攻角的飞行器升力大小不可控,只能通过单通道的滚动控制实现飞行轨迹的控制.为实现精确制导,提出了一种基于固定配平攻角飞行器的滚转制导律.建立了固定配平攻角飞行器相对目标点的运动关系方程,分析了方程中各部分的物理意义;给出了滚转制导的基本导引关系,证明了基本导引关系的正确性,得出了滚转制导指令的计算方法;通过数学仿真分析了滚转制导导引弹道的特点.仿真表明,滚转制导通过一定的滚动策略消耗掉了多余的升力,达到了精确控制飞行器落点的目的.
固定配平飞行器;滚转制导律;制导精度
可实现机动飞行控制的气动外形再入飞行器有3种[1]:一是十字舵面外形,可通过三轴的姿态控制,达到改变控制力大小和方向的目的;二是可变攻角倾斜转弯外形,它具有两轴控制的特性,通过控制再入飞行器的滚动角度,同时控制俯仰产生的升力,实现机动控制;三是固定配平攻角外形,利用再入飞行器的外形不对称或质心偏移产生不可控制的气动配平攻角,采用滚动单通道控制的方式改变配平升力的方向,实现对飞行器弹道的控制.相对于前两种气动外形,固定配平攻角外形的再入飞行器气动外形简单、控制通道少[2],但是由于它的升力大小不可控,无法实现零升力弹道,在飞行器接近目标落点时,要实现对落点精确控制需要有合适的制导律来消耗多余的升力,本文将对此进行研究.
固定配平攻角外形的再入飞行器,最早应用在飞船和空天返回式运载器上,如Gemini号飞船、Apollo号飞船以及欧洲的Space Mail capsule,它们的再入机动控制一般采用实时的路径预测法和参考弹道法[3-5].实时路径预测法通过近似求解飞行器运动微分方程或代数方程,结合飞行的限制条件,预测弹道并给出飞行器的开环控制输入.参考弹道法是事先规划一个标准再入弹道,控制飞行器在标准弹道附近飞行.这两种导引方法的落点控制精度不高,但能满足飞船的要求.美国的MK500逃逸型机动弹头[6]也采用了固定配平攻角外形,它通过弯头锥的形式产生固定配平攻角,在再入时通过控制滚动来进行机动,达到躲避敌方高性能导弹拦截的目的.但MK500仅是按预定程序飞行,它实际上是靠牺牲一定的精度来换取机动能力的.有关文献也研究过固定配平攻角外形飞行器的制导问题[1,7],但他们大都是对三轴或两轴控制飞行器制导律的简单应用,无法解决固定配平攻角外形飞行器接近目标时的升力多余问题,导致落点精度不高.
1 滚转制导律
1.1 坐标系定义
a.目标坐标系TXgYgZg
以目标点T作为坐标系原点;TXg轴在当地水平面内指北为正;TYg轴沿当地地垂线向上为正; TZg轴与上述两轴垂直并构成右手坐标系.由于再入时间较短,本文不考虑地球的自转,视目标坐标系为惯性坐标系.
b.弹道坐标系O1X¯VY¯VZ¯V
以飞行器质心O1作为坐标系原点;O1X¯V轴沿飞行器速度方向;O1Y¯V轴在包含目标坐标系TYg轴所在的铅垂平面内且与O1X¯V轴垂直,并指向上方; O1Z¯V轴与上述两轴垂直并构成右手坐标系.
1.2 滚转制导律
设飞行器的质量为M.可得如下关系式:
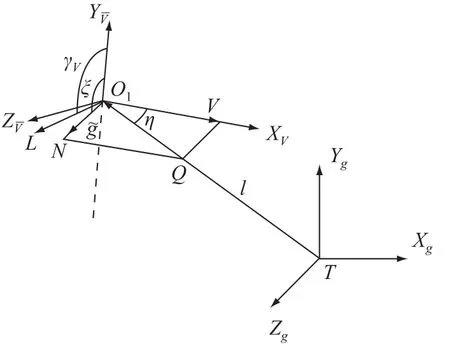
图1 滚转制导示意图Fig.1 The illustrative diagram of rolling-guidance
通过控制减小误差角η并使之趋于零,可使飞行器精确命中目标点.对于升力L大小和方向可控的弹头,可以使升力L处于误差平面内,其方向沿着使误差角η减小的方向,同时调节 L的大小,使 η趋近于零是可以实现的;但是对于固定配平的飞行器,升力L的大小不可控,若仍按上述方法,使升力L的方向处于误差平面内且沿着使 η减小的方向,当η减小到零时,由于升力 L的存在,˙η不为零,因此会产生出新的误差角,此时升力 L必须反向进行修正,如此重复.按照此种控制方式,飞行器必须快速地来回翻滚,以达到升力反向的目的,剧烈地滚动不仅对飞行器的稳定飞行不利,也会对滚动控制装置提出难以实现的要求.
分析式可知,等式右端第一项代表了无力作用时飞行器自由运动对误差角η的影响,等式右端第二项代表了地球引力作用对误差角η的影响,等式右端第三项代表了升力作用对误差角η的影响.前两项是不可调节的,要对误差角 η进行控制,只能通过调节第三项来实现.但是由于升力L的大小不可调节,要调节升力作用效果,只能通过调节升力的作用方向来实现,也即改变式(1)中cos(ξ-γV)的大小.为控制误差角η的变化,考虑使式(1)中等号右边第二项和第三项正比于第一项,即式中K定义为制导系数.

定理1.在以下条件
1)式(3)成立;
2)K>1;
3)V>0;
4)η的初值不等于π.
成立的情况下,对于由式(1)、(2)组成的微分方程组,在任何初值条件下,其解都满足(η→0,l→0),即飞行器能精确命中目标.
证明.
将式(3)代入式(1),联立式(2),得:
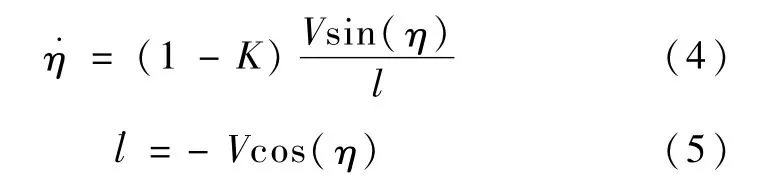
当η初值不为零且不为 π时,将式(4)除以式(5)整理可得
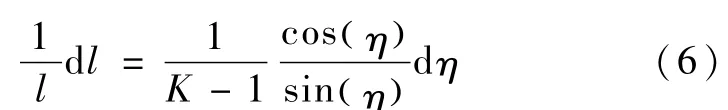
积分上式可得:
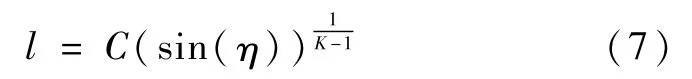
式中C>0为积分常数.
将式(7)代入式(4)整理可得
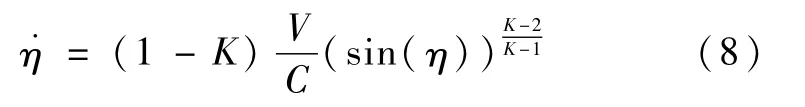
讨论1.对于η的初值等于π的特殊情况,此时代表了飞行器初始速度矢量沿视线器的速度背离目标.由式(4)可知误差角的变化率为零,即=0,η将始终保持π值.由于cos(π)= -1,由式(5)可知˙l=V>0,l将单调增加.在此情况下,飞行器将飞离目标.但在飞行器实际飞行的过程中,η=π是制导系统设计的孤立的非收敛点,即由于飞行器在飞行过程中不可避免的要受到各种干扰,使η产生摄动,从而使η≠π,此时将满足定理1的条件,使(η→0,l→0).
由定理1及讨论1可知,在实际飞行的任何初始条件下,当制导系数K>1时,导引关系式(3)都能使飞行器命中目标.
讨论2.以上的分析结果是以式(3)的成立为前提,分析式(3)可知,由于
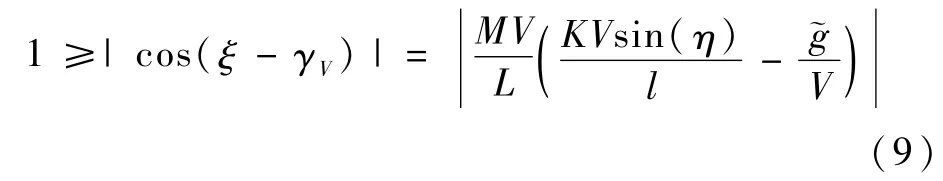
综上分析,结合式(3)可以得出制导指令 γV的确定方法

本文称按式(10)给出制导指令的方法为滚转制导律.
2 仿真分析
本节通过三自由度数学仿真分析滚转制导律导引弹道的特点以及制导精度.仿真中的再入初值如下:
速度:7000m/s;
当地弹道倾角:-10°;
高度:80km.
2.1 滚转制导典型弹道曲线
图2为固定配平飞行器再入飞行过程中误差角η的曲线.飞行器再入初段,由于气动力较小,升力对误差角η的控制能力小于飞行器自由运动和地球引力作用对误差角 η的影响,误差角 η逐渐增大;随着高度的下降,气动力逐渐增大,升力对误差角η的控制能力逐渐增大,误差角 η开始减小;当飞行器接近目标时,误差角η减小到0.24°,这保证了飞行器以较高的精度命中目标;最后时刻误差角η的突然增大是由飞行器接近目标时视线l变的很小造成的.
图3给出了速度倾侧角γV的曲线.可以看出,相应与图2的误差角曲线,当升力对误差角η的控制能力不足时,飞行器没有进行滚动,而是把升力保持在误差平面内最大限度的利用升力使误差角减小;当升力的控制能力过剩时,飞行器开始滚动以消耗多余的升力,飞行器滚动的直观表现是飞行器以螺旋式的弹道飞行(如图4所示).
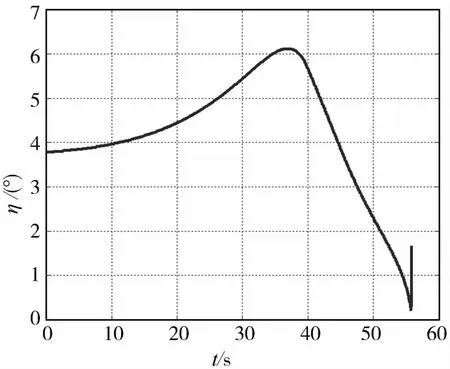
图2 误差角Fig.2 Error angle
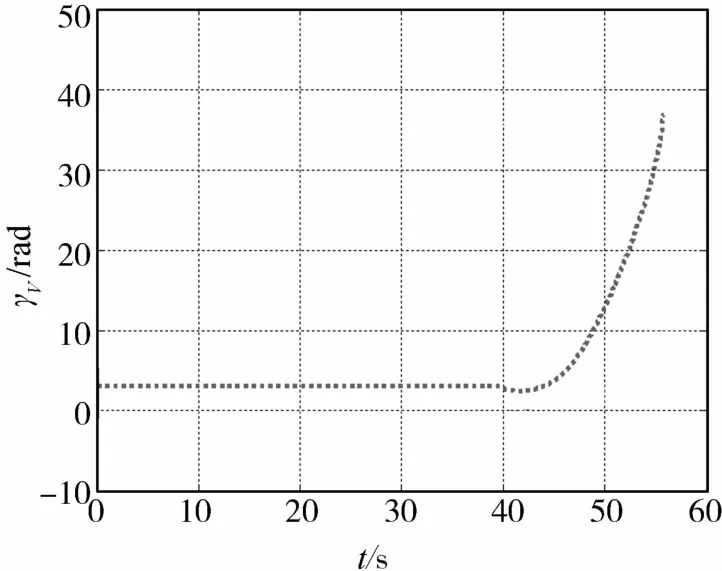
图3 速度倾侧角Fig.3 Velocity tilting angle
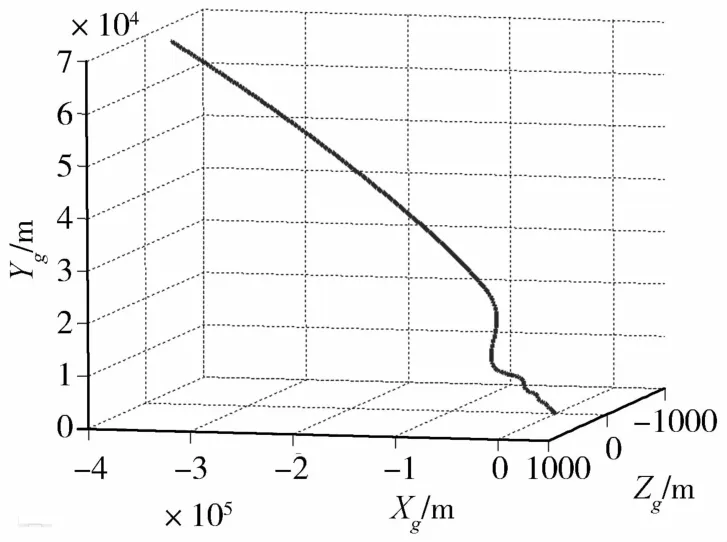
图4 目标系中的三维弹道曲线Fig.4 3D ballistic curve in the target coordinate frame
2.2 制导精度分析
当固定配平飞行器产生的固定配平攻角为3.6°时,取制导系数K为1.6,以375km为标准再入射程,目标在半径为15km的圆域内变化.图5给出了1000条随机弹道落点散布,落点的圆概率误差(CEP)为0.35m.可以看出滚转制导具有很高的制导精度.
在考虑气动阻力系数误差(最大偏差±15%)、升力系数误差(最大偏差 ±15%)、密度误差(最大偏差±15%)、质量误差(最大偏差 ±5%)的情况下,图6给出了误差随机组合情况下1000条弹道的落点散布图,其CEP为0.36m,可以看出滚转制导对各项误差具有很好的鲁棒性.
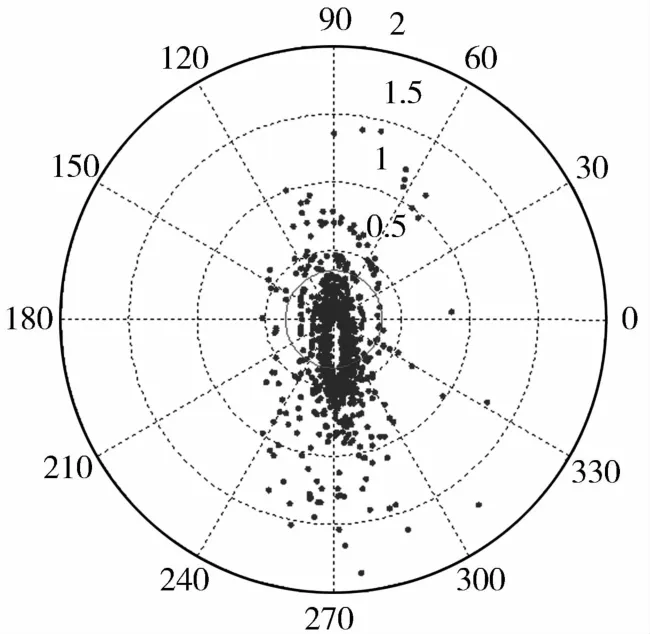
图5 无干扰情况下落点散布Fig.5 Landing point distribution without disturbance
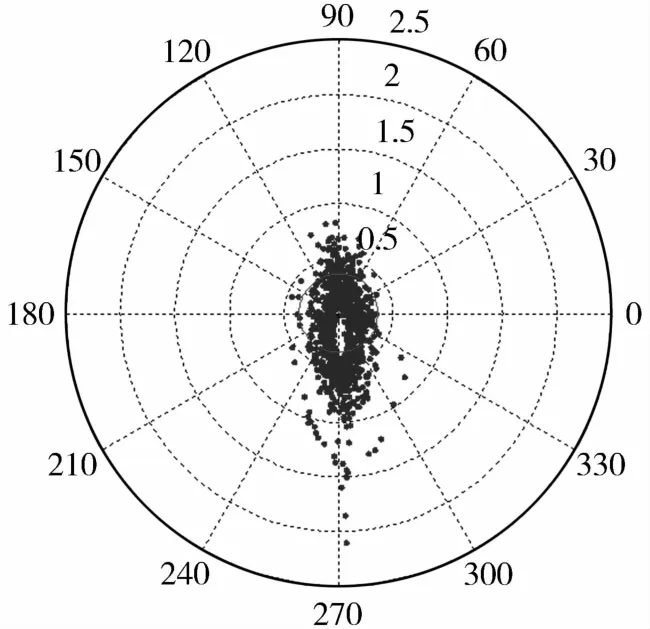
图6 干扰情况下落点散布Fig.6 Landing point distribution with disturbance
从图 5和图 6中可以发现滚转制导下落点散布存在一个有趣的现象,即在目标点附近存在一个落点的空白区.这说明通过调节固定配平升力的方向,滚转制导虽然能把多余的升力分布在各个方向上,使飞行器尽量接近目标,但是由于配平升力的旋转速率并不能无穷大,因此滚转制导并不能完全的消耗多余的升力,从而导致飞行器的落点分布在目标点的周围.
3 结 论
固定配平飞行器的升力大小不可控,无法实现零升力弹道,为合理分配升力,达到精确控制飞行器落点的目的,本文提出了一种基于固定配平飞行器的滚转制导律.通过定理证明了滚转制导导引关系的正确性,给出了滚转制导指令的计算方法.通过数学仿真验证了滚转制导律具有很高的命中精度.
[1] Page JA,Rogers R O.Guidance and control ofmaneuvering reentry vehicles[C].IEEE Conference on Decision and Control,California,Dec.1977
[2] Anon.Generic aerocapture atmospheric entry study [R].Pasadena:Jet Propulsion Laboratory,1980
[3] Rodney C,W ingrove.Survey of atmosphere re-entry guidance and controlmethods[J].AIAA Journal,1963 (9):2019-2029
[4] Roenneke A,Cornwell P.Trajectory control for a lowliftmaneuverable reentry vehicle[C].Aerospace Design Conference,Irvine,CA,Feb.1992
[5] Axel J,Klaus H.Reentry control of a low-liftmaneuverable spacecraft[C].AIAA Guidance,Navigation and Control Conference,Hilton Head Island,SC,Aug.1992
[6] Mathew B.Technology of ballistic m issile vehicles [M].Press of MIT,Cambridge,America,1984
[7] Gracey C,Cliff EM.Fixed-trim reentry guidance analysis[C].Guidance and Control Conference,Albuquerque,United States,Aug.1981
A Vehicle Rolling-Guidance Law Based on Fixed Trimm ed Angle of A ttack
LIZixing1,LIGaofeng1,HUANG Ruiling2
(1.Beijing Institute of Control and Electronic Technology,Beijing 100038,China; 2.Beijing Institute of Ximaden Automation,Beijing 100080,China)
The magnitude of lift force of reentry vehicles with fixed angle of attack is not controllable.The control of the flight path can only be achieved by roll-axis control action.In order to accurately steer the fixed angle of attack reentry vehicle,a rolling-guidance law based on fixed trimmed angle of attack (FTAA)is presented.The FTAA vehicle motion equation with respect to the target placement is established.The physicalmeaning of the motion equation is analyzed.The basic guidance method of the rolling-guidance is put forward.The correctness of the guidancemethod is proved.The calculationmethod of the rolling-guidance command is also given.The ballistic characteristic of the rolling-guidance is analyzed by a mathematical simulation.The simulation result illustrates that,by certain rolling strategy,the rolling-guidance law can consume the extra lift,achieving the accurate landing-point control of the vehicle.
fixed trimmed attack-angle vehicle;rolling-guidance;guidance accuracy
TJ765.3
A
1674-1579(2012)06-0023-04
李自行(1982—),男,工程师,研究方向为导航、制导与控制;李高风(1941—),男,研究员,研究方向为导航、制导与控制;黄瑞玲(1981—),女,工程师,研究方向为自动控制.
*部级预研资助项目.
2012-08-16
DO I:10.3969/j.issn.1674-1579.2012.06.005

