再入动力学的性质及其在轨迹优化中的应用*

王泽国，孟 斌

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

再入动力学的性质及其在轨迹优化中的应用*

王泽国1，2，孟 斌1，2

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

考虑具有终端约束和过程约束的探月返回飞行器再入轨迹设计问题，通过将性能指标泛函定义为再入终端位置误差的平方和，再入轨迹设计问题转化为具有过程约束和状态方程约束的优化问题.首先仅考虑状态方程约束，利用最大值原理，得到该优化问题的必要条件，选取间接法中的共轭梯度算法求解最优控制量.进而针对轨迹约束问题，研究了再入过载和轨道飞行段飞行距离与航迹角以及倾侧角的关系，在此基础上，提出了采用调整初始倾侧角序列的方法实现过程约束.该算法克服了罚函数方法中需要调节参数较多的问题，并且物理意义明确，实现简单.最后，给出了Apollo再入轨迹优化的数值仿真算例，验证了所给出算法的有效性.

探月返回;跳跃式再入;轨迹优化;再入动力学的性质;初值调整

近年来，探月飞行器的研究继Apollo后得到广 泛关注.对于探月返回再入轨迹规划问题，由于飞行器运动方程复杂，一般采用数值方法求解.数值方法可以分为直接法和间接法，两种方法各有优缺点[1].直接法将优化问题转化为非线性规划问题，采用某种优化算法来求解.由于飞行器运动精度要求较高，因此需要更多的离散点个数，并且直接法的初始状态难以选择，这给轨迹设计带来不便.本文考虑间接求解方法.在探月返回再入轨迹规划的间接法研究中，Istratie等[2]给出了在给定初始条件和最终条件下的最优轨迹，但未考虑过载和热流的限制.南英等[3]主要以轨迹中的过载、热流和动压的目标给出了最优轨迹，并比较不同次数再入情况下各个目标，但尚未考虑终端约束的限制.王乐等[4]给出了采用共轭梯度法设计临近空间飞行器再入轨迹的一般方法，给出了终端时刻固定的设计方法.在间接法中，当考虑过载等过程约束问题时，一般采用罚函数方法[3-4]，这将导致需要调节的参数增加，并且增加了算法收敛的难度.

本文研究探月返回飞行器有约束的跳跃式再入轨迹规划问题，轨迹约束包括终端约束、过载约束和热流约束.通过将性能指标泛函定义为再入终端位置误差的平方和，再入轨迹设计问题转化为具有过程约束和状态方程约束的优化问题.首先仅考虑状态方程约束，利用最大值原理，得到该优化问题的必要条件，选取间接法中的共轭梯度算法求解最优控制量.针对过载约束问题，通过分析过载、轨道飞行阶段飞行距离和倾侧角的关系，给出了初始控制量调节方法以实现过载约束.该算法克服了罚函数方法中需要调节参数较多的问题，并且物理意义明确，实现简单.最后，给出了Apollo再入轨迹优化的数值仿真算例，验证了所给出算法的有效性.

1 问题描述

忽略地球转动，探月返回飞行器无量纲运动方程为

对于具有低升阻比特性的再入飞船，若要求其在执行探月返回再入任务时实现长的飞行纵程，唯一可行的办法是采用跳跃式再入飞行.图 1为典型的跳跃式轨迹示意图.为了论述清晰，将跳跃式轨迹分为5段，如图 1所示.一般把高度120km作为再入起始点，再入初期空气阻力几乎为零，控制量对于飞行器的影响很弱，从120km到=0的再入初始阶段作为再入的第1阶段=0到=0段为第2阶段.假设飞行器高度第2次到达80km以上时，忽略大气的影响，飞行器以椭圆轨道运行.把飞行器第2次到达80km时称为跃出点，从=0到跃出点为第3阶段.把椭圆轨道飞行阶段称为第4阶段.第5阶段为飞行器从80km第2次再入大气层的飞行段.分别记每个阶段的起始时刻为ti，其中i表示阶段数，如图1所示.本文仅考虑在前3阶段存在一次˙=0和=0的情形，但所给出的结果可以推广到一般情形.

本文考虑探月返回飞行器受约束的跳跃式轨迹规划问题，轨迹约束包括过程约束、终端约束和控制量约束，过程约束包括过载和热流约束，终端约束为给定的飞行器的状态终值.具体地说，本文研究在给定初始状态(r0、θ0、φ0、V0、γ0和 ψ0)下，设计倾侧角变化曲线，使得飞行器再入过程满足状态方程(1)、过载限制、热流限制和倾侧角约束，并达到给定终端状态(Vf、θsite和φsite)，即满足终端约束.针对上述问题，本文研究了共轭梯度算法中轨迹约束过载的实现问题，提出了初始倾侧角序列调整的方法实现过程约束.下面首先给出倾侧角与轨迹约束过载的关系，在此基础上，给出探月返回飞行器再入轨迹优化设计方法.

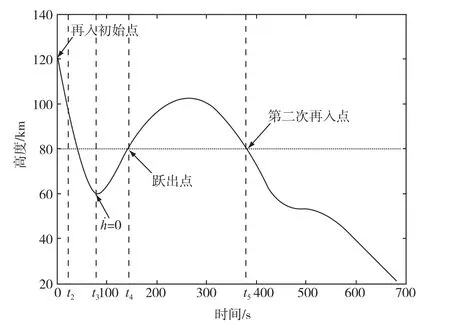
图1 跳跃式轨迹Fig.1 Skip trajectory

2 过载和第4阶段飞行距离与倾侧角的关系

本节考虑轨迹约束过载和第4阶段飞行距离与倾侧角的关系，首先考虑过载问题.由于第二次是以第一宇宙速度再入，与神舟飞船再入问题相同，因此这里主要考虑前3个阶段的过载问题.

从方程(1)可以看到，在纵向平面控制量倾侧角σ只是直接影响航迹角γ.因此，本节通过分析过载和第4阶段飞行距离与航迹角 γ的关系，以及控制量σ与航迹角γ的关系，给出过载和第4阶段飞行距离与控制量σ的关系.从而可以据此调节最优控制算法中的控制量序列.

2.1 过载和航迹角的关系

本小节分析第2、3阶段过载和航迹角的关系.过载为

其中动压q=ρV2/2.易见，由于小，动压q是过载n的主要影响因素.下面通过对动压q和航迹角γ关系的分析找到过载n和航迹角γ的关系.

引理1.针对系统(1)，˙q=0当且仅当sinγ=γth，其中，γth=2/(βV2).并且如果sinγ＞γth，那么＜0;反之亦然.

证明.为了表达简单，取q中的变量，定义

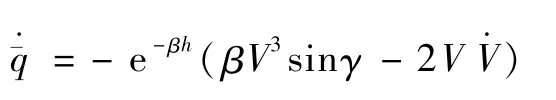
注意到 V＞0，β＞0，h＞0，以及 γth的定义，引理得证.

注意到阈值 γth是变量，下面证明在第2阶段，至少存在一个时刻，使得sinγ=γth.

引理2.针对系统(1)，关于γth的一些性质:

1)在第2、3阶段，γth＜0.

2)假设CD为常数，航迹角γ幅值较小.则在第2阶段，γth减小;第3阶段γth增大.

3)假设CD为常数，航迹角γ较小.那么在第2阶段满足如下关系:如果sinγ(t2)＜γth(t2)，则在第2阶段，存在一个时刻 tm，t2＜tm＜t3，使得sinγ(tm)=γth(tm)，其中t2和t3分别表示第2阶段的初始时刻和结束时刻;进而如果在第2阶段有 ˙γ＞0，那么sin(γ)与γth有唯一的交点.

4)假设CD为常数，航迹角γ较小.则在第3阶段sinγ＞γth.

2)当航迹角γ幅值较小时，由式(1)和Vs的定义可得，

由上式可知，如果CD为常数，那么当 ˙h＞0时，γth增大;反之亦然.亦即在第2阶段，γth减小;第3阶段γth增大.

3)由定义可知，第2阶段末端t3时刻的航迹角为0，由 1)可知，γth＜0，所以如果 sinγ(t2) ＜γth(t2)，则由各状态变量的连续性可知，在第二阶段存在一个时刻tm，t2＜tm＜t3，使得sinγ(tm)= γth(tm).进而如果第二阶段 ˙γ＞0，结合 γth单调递减，则在第2阶段sinγ与γth仅有一个交点.

4)由第3阶段γ＞0＞γth，显然得证.

由上述引理，可以得到第2、3阶段动压的性质.引理3.针对系统(1)，假设CD为常数，航迹角γ较小.如果sinγ(t2)＜γth(t2)，那么第2、3阶段的动压在第2阶段达到最大.进而如果第2阶段有 ˙γ＞0，那么第2阶段动压有唯一的极值点.证明.假设CD为常数，航迹角γ较小.由引理1和引理2，第3阶段γ＞0＞γth，则˙q＜0，因此，q(t)＜q(t3)，t3＜t＜t4，即，动压在第2阶段达到极大.进而如果第2阶段有 ˙γ＞0，由引理1和引理2，sinγ与γth有唯一的交点.也即第2阶段动压有唯一极大值点.

由引理3可知，再入过程第2、3阶段的过载最大值出现在第2阶段，我们可以将该问题归纳为极小极大问题，给出过载最大值极小的严格的理论结果.本文仅对该问题进行简单分析.为了减少过载最大值，需要增加或者减小航迹角，但是这可能导致增加高度的同时增加速度，或者减小高度的同时减小速度，因此对动压产生复杂的影响.

动压与高度和速度均相关，由式(1)可知，航迹角对于速度和高度具有相反的作用，因此对于动压的影响较复杂.下面通过比较3组具有不同高度和速度的状态(hm，Vm)、(hm(1+a)，Vm)和 (hm，Vm(1-b))的动压值，给出航迹角对于动压的影响关系.实际中轨迹的高度与速度的变化不超过50%，即a∈(0，0.5)，b∈(0，0.5).分别记三组状态所对应的动压分别为qm、qm1、qm2.则

假设动压最大值出现在高度为60km左右，则e-βhm约为6.85×10-4.如果qm1=qm2，则有b=1-0.0262a.当a∈(0，0.5)时，b＞a，即如果动压改变相同量，则速度减小幅度要大于高度增加幅度，因此高度增加对减小动压更加有效.所以在第2阶段通过增大航迹角，增加高度，可以有效减小动压极值.

2.2 第4阶段飞行距离和航迹角的关系

按照第1节的定义，把椭圆轨道飞行阶段称为第4阶段，如图1所示.一般来说第4阶段飞行器处于不受控的状态，本部分讨论该段飞行距离和航迹角的关系，从而给出控制量倾侧角对于第4阶段飞行距离的影响关系.

引理4.假设飞行器高度第2次到达80km以上时，忽略大气的影响，飞行器以椭圆轨道运行，跃出点速常数.则第4阶段飞行距离与跃出点航迹角正相关.证明.由假设，飞行器高度第二次到达80km以上时，忽略大气的影响，飞行器以椭圆轨道运行.下面由跃出点真近点角与跃出点航迹角的关系，得出第4阶段飞行距离与航迹角的关系.由文献[6]可知，跃出点飞行器的真近点角ϑt(如图2所示)满足

下面证明

由式(2)，求得cosϑt关于航迹角γt的导数

图2 跳跃式再入轨迹Fig.2 Skip reentry trajectory

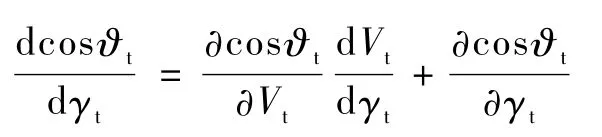
由假设、式(1)及γt较小，忽略阻力D和sinγt，得

由于ϑt＞90°，所以cosϑt＜0.由于Ct＜1＜1/cosγt＜1/cos2γt，可得

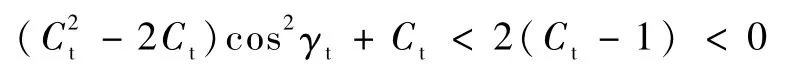
和

因为γt为大于0的较小值，我们有

结合上面的结果，可得

即cosϑt与γt正相关，ϑt与γt负相关.由于第4阶段飞行距离与ϑt负相关，所以第4阶段飞行距离与γt正相关.

由上述引理可知，第4阶段飞行距离与航迹角γt正相关.而第4阶段飞行距离一般是确定的，也就是跃出点航迹角γt不能有较大变化.

2.3 过程约束与倾侧角的关系

2.1 和2.2中分析了过载和第4阶段飞行距离和航迹角的关系，本部分首先分析倾侧角和航迹角的关系，进而给出过程约束与倾侧角的关系.

由cosγ≈1、1/r≈1，和式(1)可得

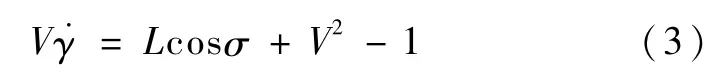
由于倾侧角可以在-180°至180°之间变化，cosσ∈[-1，1]，若L＞V2-1，那么倾侧角的选择会影响航迹角的导数符号，我们说倾侧角对于航迹角有主要影响.

引理5.假设升力系数CL是常数.则当V＞1，h＜导数的符号可以由倾侧角的幅值控制.

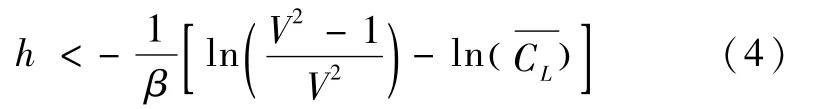
时，L＞V2-1.由式(3)可知，当L＞V2-1时，航迹角的导数的符号可以由倾侧角的幅值控制.由于ln(V2)-ln(V2-1)＞0，可知若V＞1，h＜

通过将常数CL=0.4717及仿真中表1的常数可估算出当 V＞1，高度小于68.92km时倾侧角的调整对于航迹角起主要作用.实际上所忽略的[ln(V2)-ln(V2-1)]/β对于高度估计也有影响，所以在更高的高度就可以使得控制量起主要作用.而且由于在较低高度的阻力很大，使得速度迅速下降，这样使得以后的控制量一直占主要影响.

综合上述分析，可以考虑减小第1阶段和第2阶段的倾侧角，并增加第3阶段的倾侧角，以减小动压极大值并保证轨道飞行阶段的飞行距离.

轨迹约束中关于热流的限制问题也是需要注意的.但由于热流最大值一般出现在再入初始阶段，因此控制量的选取对于热流的影响较小[7]，所以不对热流限制做单独设计.

3 最优轨迹规划

本节考虑探月返回飞行器受约束的跳跃式轨迹规划问题.通过将性能指标泛函定义为再入终端位置误差的平方和，再入轨迹设计问题转化为具有过程约束和状态方程约束的优化问题.首先仅考虑状态方程约束，利用最大值原理，得到该优化问题的必要条件，选取间接法中的共轭梯度算法求解最优控制量，利用上节给出的倾侧角和过程约束的关系，通过调整初始控制量序列以满足过程约束.

选择目标泛函为飞行器的终端经度 θf和纬度φf与目标点(θsite，φsite)的差的平方和J=k1(θfθsite)2+k2(φf-φsite)2最小[4]，其k1和k2为待定常数.则Hamiltonian函数为

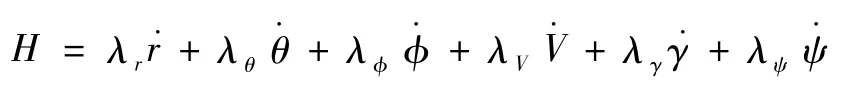
其中λr，λθ，λφ，λV，λγ，λψ为相应的协态变量.根据最大值原理，可得协态变量满足:

协态变量的终值为

其他终值为零;最优控制量σ满足

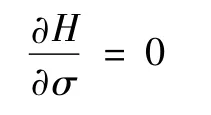
和控制输入约束.

下面采用共轭梯度法，求解上述无过程约束问题.共轭梯度法的主要思想是先给出一组初始控制量序列，在每次迭代中计算Hamiltonian函数关于控制量的偏导，控制量沿着令Hamiltonian函数减小的方向，最后达到使得目标泛函最小的最优解[8-9].

上述算法中需要调节的主要是初始控制量σ0.初始控制量序列σ0的选择根据第2节的结果进行调节，首先选取某个常数序列使得飞行器的纵程误差较小，并且算法收敛，然后通过翻转实现横程调节，进一步通过调整第2阶段的倾侧角降低过载，增加精度.

4 数值仿真

本节针对探月返回飞行器Apollo，利用初值选取原则和共轭梯度法设计受限再入轨迹.Apollo的参数和给定的初始状态和终端状态见表 1.飞行器在运行中需要考虑过载、热流和控制输入的限制.在文献[7]中给出了几类过载限制，分别是正常乘员逃生时的最大过载，正常乘员再入时的最大过载，和受伤乘员承受的最大过载.这里采用其中最严格的限制，即受伤乘员承受的最大过载.仿真中考虑了热流的限制[10](见表 1)，控制量的限制为 -180°≤σ≤180°.

下面按照第3节的算法给出再入轨迹，通过初始控制量序列调节方法以满足过载约束.首先选择一常数控制量序列，然后通过尝试得到飞行器翻转时刻，具体设计为常值倾侧角-45°，在时刻85s翻转.通过优化，飞行器刚进入大气层时过载比较大，在10s附近与乘员能够承受的最大过载重合.

下面通过调整初始控制量的方式来减少过载.由2.3节的结论，选择再入初始时较小的倾侧角幅值和跃出点较大的倾侧角幅值，第2次再入后选择一个飞行器翻转时刻以达到横向控制.采用这种控制策略，经过试验调节，可以得到过载和落点误差更小的轨迹.图 3为修改后的初始倾侧角序列，再入初始时倾侧角为零，然后迅速上升至180°以防止飞行器椭圆轨道飞行距离过大，接着按 9°飞行，在700s翻转.图4是优化后的倾侧角变化曲线，得到仿真结果如图 5～7所示.由图 5可见过载明显降低，最大过载由9.8832g降至7.2557g，满足过载约束.由图 6可见开伞点与期望点几乎重合，误差为8.2050km，与调整前相比明显减少.从图7可见算法收敛较快.热流的最大值为1.7242×105W/m2，低于表1中要求的热流最大值.

表1 常数Tab.1 Constants

图3 调整后初始控制量序列Fig.3 Initial control profile after ad justment

图4 优化后控制量序列Fig.4 Optimized control profile

图5 过载和限制Fig.5 Overload and limit

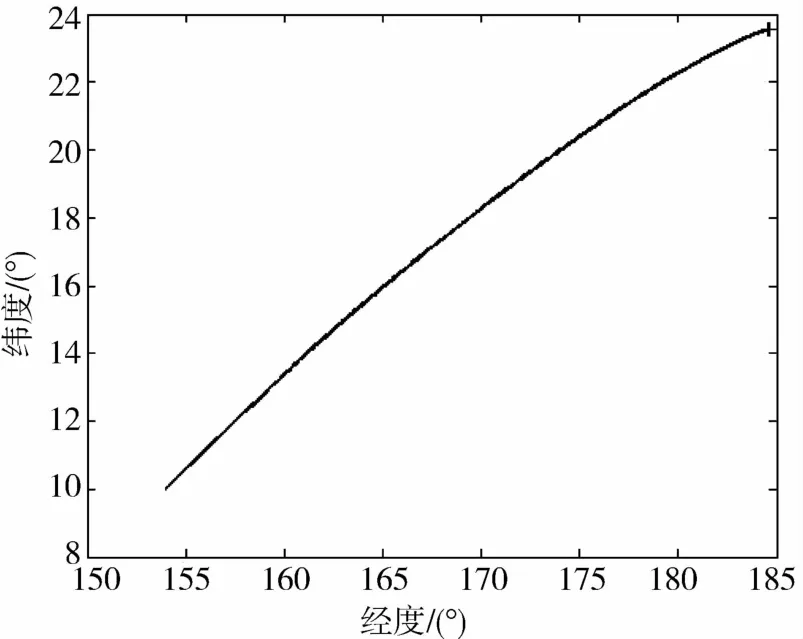
图6 飞行器的经纬度变化Fig.6 Latitude and longitude of the vehicle

图7 性能指标变化曲线Fig.7 Performance index curve

5 结 论

本文考虑探月返回飞行器受限轨迹规划问题.研究了过载和轨道飞行段飞行距离与倾侧角的关系，给出了过载极值与航迹角的关系和轨道飞行段飞行距离与跃出点航迹角的关系，以及控制量倾侧角与过程限制的关系.在此基础上，给出了共轭梯度算法过程限制的初始控制量序列调节方法.最后通过数值仿真给出了满足约束的Apollo再入最优轨迹，表明所给出算法的有效性.

[1] Betts J.Survey of numerical methods for trajectory optimization[J].Journal of Guidance，Control，and Dynamics，1998，21(2):193-207

[2] Istratie V.Optimal skip entry into atmosphere with minimum heat and constraints[C].AIAA Atmospheri Flight Mehanis Conferene，Denver，2000

[3] 南英，陆宇平，龚平.登月返回地球再入轨迹的优化设计[J].宇航学报，2009，30(5):1842-1847 Nan Y，Lu Y P，Gong P.Optimal reentry trajectory design for mooncraft returning to the Earth[J].Journal of Astronautics，2009，30(5):1842-1847

[4] 王乐，方群，欧岳峰.临近空间飞行器再入轨迹优化设计[J].科学技术与工程，2011，11(3):543-547 Wang L，Fang Q，Ou Y F.The optimization design of the near space vehicles're-entry trajectory[J].Science Technology and Engineering，2011，11(3):543-547

[5] U.S.national oceanic and atmospheric administration，US standard atmosphere[R].Washington，D.C.:U.S.National Oceanic and Atmosphemic Administration，1976

[6] 耿长福.航天器动力学[M].北京:中国科学技术出版社，2006:273-275 Geng C F.Spacecraft dynamics[M].Beijing:China Science and Technology Press，2006:273-275

[7] Bairstow S，Barton G.Orion reentry guidance with extended range capability using PredGuid[C].AIAA Guidance，Navigation and Control Conference and Exhibit，Hilton Head，2007

[8] Bryson A E，Ho Y C.Applied optimal control[M]. Waltham，Mass.:Blaisdell，1969

[9] 宫锡芳.最优控制问题的计算方法[M].北京:科学出版社，1969:97-104 Gong X F.Computation methods on optimal control problems[M].Beijing:Science Press，1969:97-104

[10] Xue S，Lu P.Constrained predictor-corrector entry guidance[J].AIAA Guidance，Control，and Dynamics，2010，33(4):1273-1281

Properties of Reentry Dynam ics and Their App lication in Trajectory Op tim ization

WANG Zeguo1，2，MENG Bin1，2
(1.Beijing Institute of Control Engineering，Beijing 100190，China; 2.Science and Technology on Space Intelligent Control Laboratory，Beijing 100190，China)

The reentry trajectory optim ization problem with term inal constraints and path constraints of a lunar return vehicle is considered in this paper.By defining the performance index function as a square sum of the reentry term inal position errors，the reentry trajectory design problem is transformed into the optimization problem with terminal constraints and state equation constraints.First，in the presence of the state equation constraints only，the necessary conditions of the optim ization problem are obtained by using the maximum principle，and the optimal control is solved using the conjugate gradientmethod.Then，in the presence of path constraints，we have studied the relationship among the overload，the distance of the orbit phase，the flight path angle and the bank angle.Based on the above，amethod of initial bank angle value ad justment is presented to satisfy the path constraints.This approach，with definite physicalmeaning and simple implementation，circumvents the shortcoming of the punishment-functionmethod which involves too many ad justed parameters.Finally，a numerical example for Apollo reentry trajectory optimization is given to illustrate the effectiveness of the algorithm.

lunar return;skip reentry;trajectory optim ization;property of reentry dynam ics;initial value adjustment

V448.235

A

1674-1579(2012)06-0006-07

王泽国(1988—)，男，硕士研究生，研究方向为航天器再入制导;孟 斌(1973—)，女，高级工程师，研究方向为航天器控制.

*国家自然科学基金资助项目(61273153，60736023，60704014).

2012-08-03

DO I:10.3969/j.issn.1674-1579.2012.06.002