CFRP中孔隙几何形貌与超声衰减系数关系的研究

高晓进，张 峥

（北京航空航天大学材料科学与工程学院，北京100191）

CFRP中孔隙几何形貌与超声衰减系数关系的研究

高晓进，张 峥

（北京航空航天大学材料科学与工程学院，北京100191）

通过金相和超声衰减系数表征CFRP层压板中的孔隙，研究孔隙形貌对超声衰减的影响。结果表明：超声衰减系数随孔隙几何形貌参数（平均长、宽、面积）的增大而增大；平均孔隙长度随孔隙率的增加程度大于平均孔隙宽度随孔隙率的增加程度；超声衰减系数随主要尺寸区域内的孔隙所占比例的增加，总体趋势减小；同一孔隙率下，大尺寸孔隙所占的比例越多，其超声衰减系数越大。总之，本试验中孔隙形貌对超声衰减有一定的影响且不能忽略。

超声；衰减系数；孔隙；形貌

孔隙是复合材料中最为常见、最为重要的缺陷之一［1，2］。CFRP（炭纤维增强树脂基复合材料）中通常含有孔隙缺陷。其尺寸范围为几微米到几百微米。

孔隙的形状、大小和体积分数对复合材料的力学性能有重要影响［3－5］。研究表明［6，7］，每增加1%的孔隙率，复合材料的层间剪切性能下降5%～15%不等，直到孔隙率达到4%，这种规律基本保持不变。刘志真［8］在研究孔隙率对聚酞亚胺复合材料力学性能的影响时，得出：随着孔隙率的增加，弯曲强度逐渐下降，在孔隙率小于1%时，弯曲性能相差不大，弯曲强度的保持率为90%左右，当孔隙率大于3%时，弯曲强度的下降趋势趋于平缓，弯曲强度保持率大约只有75%。

超声检测是一种常用的检测复合材料中缺陷的无损检测方法。CFRP中孔隙的尺寸很小，用超声无损检测的方法无法准确确定单个孔隙的位置和大小。超声C扫描也不能检测出其具体形貌。文献［9，10］通过测量CFRP材料对超声的衰减系数，再建立超声衰减系数与CFRP材料中孔隙率的关系，达到孔隙率的超声无损检测的目的。但该方法在建模时，假设孔隙为球形、椭球形或圆盘形等规则形状，且孔隙为均匀分布，忽略孔隙形貌对超声衰减的影响，孔隙率测量值与实际值有一定的误差。可能的原因是模型中引入的孔隙形貌与实际情况不符。

因此本工作主要研究CFRP中孔隙形貌对超声衰减的影响，主要包括三个方面：（1）孔隙几何形貌参数（平均长、宽、面积）与超声衰减系数的关系；（2）孔隙几何形貌参数（孔隙长度）的分布对超声衰减系数的影响；（3）孔隙几何形貌参数（孔隙长度）的分布对超声衰减系数与孔隙率之间关系的影响。研究结果为超声方法检测复合材料中的孔隙提供一定的支持。

1 试验过程与试验原理

1．1 试验过程

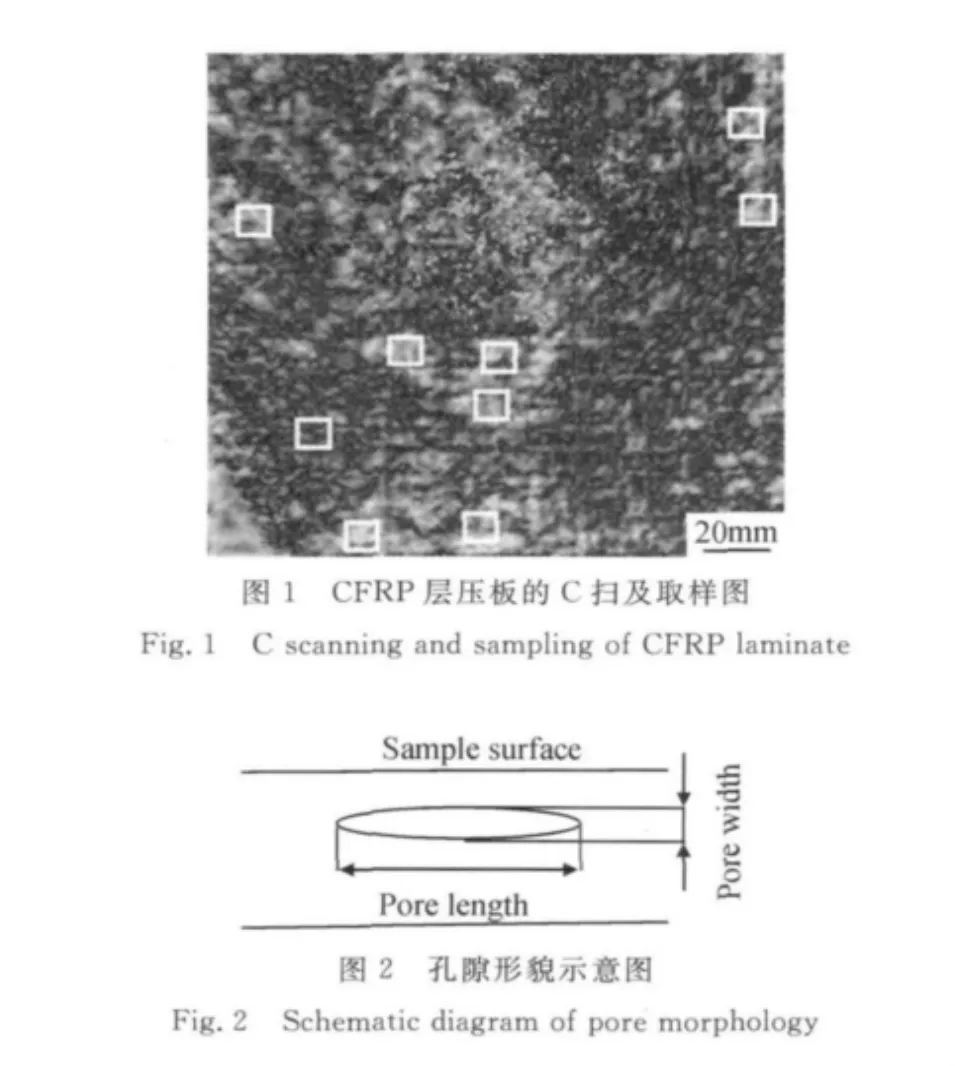
采用抽真空处理工艺，制备16层H氏预浸料准各向铺层4mm厚的CFRP层压板。然后对板进行超声C扫描，选取C扫图像中9个颜色较均匀的区域，对板上对应的区域取9个试样，如图1所示。再利用脉冲反射法测量9个试样的超声衰减系数。然后制备每个试样的纵剖面金相。如图2所示，定义孔隙平行于试样表面的方向为长度方向，垂直试样表面的方向为宽度方向，分别统计每个孔隙的长度、宽度及面积，计算试样的孔隙率。探索试样的平均孔隙尺寸与超声衰减系数的关系，孔隙长度分布与超声衰减系数的关系，及孔隙形貌如何影响超声衰减系数与孔隙率之间的关系。

1．2 试验原理

1．2．1 超声衰减系数测量

利用水浸聚焦探头超声波脉冲反射法测量超声衰减系数。如图3所示。

探头发出超声波，在耦合剂和复合材料中传播，经过复合材料板的上下两个表面的反射，被探头接收。根据超声波的衰减、反射、透射规律［11，12］，计算传播过程中的声压，通过各声压之间的关系求出复合材料的超声衰减系数的数学表达式：

αt＝10［lg P2′／P7′＋lg（R2－1）R′／R］／t［13］。式中的P2′，P7′指复合材料试样上下表面反射声压，它与超声A扫信号中对应的波高H2′，H7′成正比；R，R′指复合材料试样上下表面的声压反射系数；t指试样的厚度。所以通过测出复合材料试样上下表面对应A扫信号的波高、上下表面的声压反射系数和试样的厚度，就可以求出超声衰减系数的值。

图3 超声的传播路径Fig．3 Path of ultrasonic propagation

实际测量超声衰减系数时，由于条件限制，需要作简化处理。具体测量步骤是：将试样上下表面打磨光滑直至5000＃砂纸的粗糙度，使所有试样上下表面的声压反射系数相同，用公式计算不同试样的超声衰减系数时公式中后面一项lg（R2－1）R′／R都相同，所以只需用10［lg H2′／H7′］／t计算相对超声衰减系数。由于CFRP层压板加工工艺、材料体系种类和试样厚度较厚的原因，试样对超声的衰减较大，导致在测量时表面波高H2′可测时，底波高H7′太小，难以测量。提高并统一增益，使得底波H7′可测，此时表面波的高度超过100%，无法测量。利用增益值换算出表面波的值H2′＝1600．45%，用10［lg1600．45／H7′］／t算出试样中某点的超声衰减系数，取试样中的100个点求平均值得出每个试样的平均超声衰减系数，近似为试样的超声衰减系数。

1．2．2 孔隙形貌参数的统计

制备9个试样的纵剖面金相，拍摄100倍时的金相照片，用AUTO－CAD软件统计选取的金相照片中每个孔隙的长度，宽度和面积的值。做出每个试样的孔隙尺寸的分布直方图。

1．2．3 孔隙率的计算

用AUTO－CAD软件计算出每个试样金相照片中CFRP材料的剖面面积，和其中所有孔隙的面积和，后者除以前者的值为试样的平均孔隙率。

2 试验结果与讨论

将计算和统计的数据填入表1。表1中包括超声衰减系数、孔隙率、平均孔隙尺寸和主要孔隙长度区域内的孔隙所占比例。

表1 各参数的值Table 1 Value of each parameter

2．1 平均孔隙尺寸和超声衰减系数的关系

本文中孔隙尺寸是指孔隙长度、宽度和面积。以每个试样的平均孔隙长度、平均孔隙宽度和平均孔隙面积为横坐标，以每个试样的超声衰减系数为纵坐标作图4，5，6，并做直线拟合。从图4，5，6中发现：超声衰减系数随平均孔隙长度、平均孔隙宽度和平均孔隙面积的增加，总体趋势增加。形成这种关系的原因是：平均孔隙长度、平均孔隙宽度和平均孔隙面积都代表孔隙的尺寸，孔隙的尺寸越大，孔隙造成的超声在材料中传播时的衰减量越大，超声衰减系数也越大。

图4 平均孔隙长度与超声衰减系数的关系Fig．4 The relation between pore average length and ultrasonic attenuation coefficient

2．2 孔隙长度和宽度随孔隙率变化的比较

以试样的孔隙率为横坐标，试样的平均孔隙长度和平均孔隙宽度为纵坐标作图7，8，并做直线拟合。由图7，8可知，平均孔隙长度随孔隙率的变化范围为40～140μm，平均孔隙宽度随孔隙率的变化范围为25～50μm，所以平均孔隙长度随孔隙率增加的程度大于平均孔隙宽度随孔隙率增加的程度。可能的原因是：复合材料在制备过程中受到的纵向压力大于横向压力，使得孔隙在横向扩展比纵向扩展容易，即孔隙长度方向上的扩展易于孔隙宽度上的扩展。由上述可知，超声衰减系数随孔隙长度变化的敏感性要高于随孔隙宽度变化的敏感性。此外，孔隙的面积取决于孔隙长度和孔隙宽度的值。因此，在下面的讨论中，只研究孔隙尺寸中孔隙长度这一个方面，不考虑孔隙宽度和孔隙面积。

2．3 孔隙长度分布和超声衰减系数的关系

图9为6＃试样中孔隙长度的分布直方图。以每个试样中在主要孔隙长度分布区域（10～100μm）内的孔隙占所有孔隙数量的比例为横坐标，超声衰减系数为纵坐标作图10，并做直线拟合。从图10中发现：超声衰减系数随主要孔隙长度分布区域（10～100μm）内的孔隙所占比例增加，总体趋势下降。形成这种关系的原因是：试样中主要孔隙长度分布区域内的孔隙长度范围为10～100μm，孔隙长度值很小。主要孔隙长度分布区域内的孔隙所占比例越大，较大孔隙占的比例越小，试样中孔隙的总面积和越小，孔隙造成的超声在材料中传播时的衰减量越小，超声衰减系数也越小。

图9 6＃试样的孔隙长度分布图Fig．9 Pore length distribution of 6＃specimen

图10 主要孔隙长度分布区域内的孔隙所占比例与超声衰减系数的关系Fig．10 The relation between proportion of pores in region of main pore length and ultrasonic attenuation coefficient

2．4 超声衰减系数与孔隙率的关系及影响因素

以2＃～9＃试样的孔隙率为横坐标，超声衰减系数为纵坐标作图11，并做直线拟合。令孔隙率P和超声衰减系数α的线性关系式为α＝a＋b·P，其中a，b为系数。用最小二乘法求系数a，b：将2＃～9＃试样的孔隙率P和超声衰减系数α的值代入到方程∑9n＝2（α－a－b·P）2＝0中，并分别对方程中的a，b求偏导，得到二元一次方程组，求出a，b的值，得出P与α的线性函数关系式为α＝4．025＋0．093P。

由函数关系式和图11可知，拟合的超声衰减系数随孔隙率的变化趋势与STONE［14］研究结果一致。但前人在研究超声衰减系数与孔隙率之间关系时，假设孔隙为球形，椭球形或圆盘形等规则形状且形貌一致，忽略孔隙形貌对超声衰减系数与孔隙率之间关系的影响，没有从孔隙形貌对超声衰减系数与孔隙率之间关系的影响方面进行研究。以下从孔隙形貌对超声衰减系数与孔隙率之间关系的影响方面进行研究。

图11 孔隙率与超声衰减系数的关系Fig．11 The relation between porosity and ultrasonic attenuation coefficient

将根据2＃～9＃号试样数据作的孔隙率－超声衰减系数图中的相邻点连接，得图12。图中3＃和9＃点出现异常：该两点的纵坐标值高于相邻的值，且远高于相邻两点的均值。为探索原因，做出以下分析：

图12 孔隙率与超声衰减系数的关系（连接相邻点）Fig．12 The relation between porosity and ultrasonic attenuation coefficient（connecting adjacent points）

根据每个试样的孔隙长度分布直方图，可知试样2＃～9＃中，孔隙长度的主要分布区域为10～100μm，其中长度为400～1100μm区域内的孔隙，尺寸大，分布较少。为研究较大孔隙长度分布对超声衰减的影响，计算出长度为400～1100μm区域内所有孔隙长度与其百分比（不含百分号）的乘积之和，令其为纵坐标（用∑表示），孔隙率为横坐标，连接相邻点，作图13。发现纵坐标∑随孔隙率增大总体上增大，但3＃试样的纵坐标∑值很大，对应的图12中的超声衰减系数很大，9＃试样的∑值大于相邻的2＃和4＃，其对应的图12中的超声衰减系数大于相邻的2＃和4＃试样的超声衰减系数。说明在同一孔隙率时，较大孔隙尺寸的分布对超声衰减有很大的影响；较大孔隙尺寸分布的越多，超声衰减系数越大。因此，本试验中孔隙形貌对超声衰减系数与孔隙率之间的关系有较大的影响，不能忽略。

图13 孔隙率与∑的关系Fig．13 The relation between porosity and∑

孔隙形貌对超声衰减系数有一定的影响且本试验中该影响不能忽略。孔隙形貌与超声衰减系数的定量关系，将在今后的研究中进行。

3 结论

（1）超声衰减系数随孔隙几何形貌参数（平均长、宽、面积）的增大而增大。

（2）平均孔隙长度随孔隙率的增加程度大于平均孔隙宽度随孔隙率的增加程度。

（3）超声衰减系数随主要孔隙长度分布区域内的孔隙所占比例的增加，总体趋势下降。

（4）同一孔隙率下，大尺寸孔隙分布的越多，其超声衰减系数越大。本试验中，孔隙形貌对超声衰减系数与孔隙率之间的关系有较大的影响，不能忽略。

［1］ JEONG H．Effects of viods on the mechanical strength and ultrasonic attenuation of laminated composites［J］．Journal of Composite Materials，1997，31（3）：276－292．

［2］ 周晓军，游红武，程耀东．含孔隙碳纤维复合材料的超声衰减模型［J］．复合材料学报，1997，14（3）：99－106．

［3］ JUDD N C W，WRIGHT W W．Voids and their effects on the mechanical properties of composites［J］．Sample Journal，1978，14（1）：10－14．

［4］ HAGSTRAND P O，BONJOUR F，MANSON J A E．The influence of void content on the structural flexural performance of unidirectional glass fiber reinforced polypropylene composites［J］．Composites，Part A：Applied Science and Manufacturing，2005，36（5）：705－714．

［5］ CASAL E，GRANDA M，BERMEJO J．Influence of porosity on the apparent interlaminar shear strength of pitch based unidirectional C－C composites［J］．Carbon，2001，39：73－82．

［6］ BOWLSE K H，FRIMFONG S．Void effects on interlaminar shear strength of unidirectional graphite－fiber－reinforced composites［J］．Journal of Composites Materials，1992，26（10）：1487－1509．［7］ GHIORSE S R．Effect of void content on the mechanical properties of carbon／epoxy laminates［J］．Sampe Quaterly，1993，24（2）：54－59．

［8］ 刘志真，李宏远，益小苏．孔隙率对聚酞亚胺复合材料力学性能的影响［J］．材料工程，2005，（9）：57－58．

［9］ 周晓军，莫锦秋，游红武．碳纤维复合材料分布孔隙率的超声衰减检测方法［J］．复合材料学报，1997，14（3）：107－113．

［10］ 刘继忠，周晓军，华志恒．碳纤维复合材料孔隙率的脉冲反射发超声衰减测试模型［J］．浙江大学学报，2006，40（11）：1879－1881．

［11］ 史亦伟．超声检测［M］．北京：机械工业出版社，2005．19－31．［12］ 中国机械工程学会无损检测分会．超声波检测［M］．北京：机械工业出版社，2000．20．

［13］ 宋立军．复合材料孔隙率检测方法及其实现技术的研究［D］．杭州：浙江大学，2005．32－33．

［14］ STONE D E W，CLARKE B．Ultrasonic attenuation as a measure of void content in carbon－fiber reinforced plastics［J］．NDT，1975，8（3）：137－139．

Research of the Relationship Between Pore Morphology and Ultrasonic Attenuation Coefficient in CFRP

GAO Xiao－jin，ZHANG Zheng
（School of Materials Science and Engineering，Beihang University，Beijing 100191，China）

Pores in CFRP samples were characterized by metallography and ultrasonic attenuation coefficient．The effect of pore morphology on ultrasonic attenuation was researched．The results show that ultrasonic attenuation coefficient is increasing with the increase of pore geometric morphology parameter；the slope of average pore length－porosity is bigger than of width－porosity；ultrasonic attenuation coefficient is decreasing with the increase of the percentage of pores in main sizes；ultrasonic attenuation coefficient is increasing with the increase of the percentage of big pores at the same porosity．In short，the pore morphology has some influence on ultrasonic attenuation and can not be ignored．

ultrasonic；attenuation coefficient；pore；morphology

TB553

A

1001－4381（2012）07－0059－05

2011－08－15；

2011－11－29

高晓进（1987—），男，硕士研究生，主要研究方向为无损检测、材料失效分析及预测预防，联系地址：北京市海淀区学院路37号北京航空航天大学1系8研（100191），E－mail：gao19870311＠163．com

张峥，教授，主要从事失效分析预测预防研究，联系地址：北京市海淀区学院路37号北京航空航天大学1系8研（100191），E－mail：zhangzh＠buaa．edu．cn