铁路大体积混凝土热学参数反分析研究

李东磊，李化建，安明喆，孙学奎

(1.北京交通大学 土木与建筑工程学院，北京 100044;2.中国铁道科学研究院 铁道建筑研究所，北京 100081;3.京沈铁路客运专线 辽宁有限责任公司，辽宁 沈阳 110006)

1 热传导反分析发展概述

在高速铁路工程建设当中，严寒地区大体积混凝土结构在浇筑前期水化升温迅速，加之恶劣的气候条件(温差大)、露天的服役环境、自身不良的热工性能，表面常出现不规则裂缝。研究严寒地区温度场变化规律，获取与工程实际相符的热学参数，利用现代数值计算方法对构件温度场进行分析研究，在施工期采取合理的温控措施，预防温度裂缝的产生成为解决这一问题的重要手段。传统试验获取参数的方法，在准确性、时间积累特性等方面已经不能满足需要，利用数学理论进行反分析成为重要途径。20世纪80年代热传导主要针对的是一维问题，随着计算机技术的发展和有限元、边界元、无限元等理论的完善，热传导问题逐渐扩展到三维领域，识别参数也由单一变量扩展到多宗量识别，同时研究者对于参数的研究方向也由起初的导热系数和边界热流转移到了换热系数、内热源。同时，反分析理论也得到了迅速发展，最初出现的是穷举法、蒙特卡洛法［1］等完全非线性的搜索方法。穷举法需要对全部空间进行搜索，计算量大，在实际应用当中受到限制。而蒙特卡洛法则在解空间随机进行搜索，盲目性大而且难以做到全局准确实现。针对此种现象，研究者将数学优化理论引入反分析体系，基于最小二乘法［2］、Markov链、最大似然估计以及 Bayesian公式［3］等建立目标函数，通过两种途径实现参数识别。一种是建立迭代逼近机制，即设置迭代格式逐次逼近真值，主要的方法包括最快下降梯度法、牛顿—高斯法［4］、超松弛逐次迭代法［5］、正则化梯度法［6］等;另一种是建立区域搜索机制，即通过设置搜索规则快速实现识别，主要的方法包括单纯形加速法［7］、轮换模式搜索法、线性规划法、Powell法等。然而，这两类方法都属于局部收敛的方法，识别精度对于初值质量依赖性大，算法的稳定性也不理想。近年来随着研究的不断深入，仿真智能算法成为目前该领域的研究热点，取得了大量研究成果。仿生智能算法是借鉴自然界的工作机理和优选制度所建立起来的新型搜索方法，通过算子和概率转移模拟生物行为对初始群体进行操作。此类方法在应用方面很快得到了推广，但仍存在一些问题，比如对于初始种群的依赖、收敛速度、搜索停滞等问题。各种优化方法之间组合形成的混合法成为解决这一问题的主要途径。混合法可以借鉴不同优化方法的优势，代表性的方法有遗传—蚂蚁法、免疫—蚂蚁法［8］、微粒群—蚁群法等［9］。虽然针对某种算法的理论已经有人进行了整理，但关于热传导系统介绍的综述性文献还尚未见到，本文从实现机理出发对热传导反分析方法整理归类，阐述了实现方法的关键技术，并将基于网格划分的连续域蚁群算法应用于高速铁路工程，获得了良好的识别效果，为研究高速铁路混凝土温度开裂问题奠定了基础。

2 逆法

逆法是指根据实际对数学模型进行简化，通过直接求解逆方程而得到有关参数的显示表达形式的方法，结合相应的试验数据就可以得到热学参数，算法简单易于实现，但其在实现上经常遇到一些数学上的难题，在解决非线性等复杂问题时计算稳定性不好，在实际应用中受到较大限制。

逆法主要包括两种方法，一是朱伯芳提出的方法，二是黄达海等提出的划分区间计算方法。在研究混凝土温度作用关系的基础上，朱伯芳院士提出了利用表面温度数据反求热学参数的方法［10］。黄达海等［11］深入研究了“温度变化—混凝土表层温度响应”规律，得到了表层混凝土温度变化理论解，具体反分析实现步骤如下:①线性化区间;②优选测点;③反演计算。

3 正法

由于逆法在实际应用中受到诸多条件的限制，而且所得数据离散、代表性不强。现在，关于混凝土热学参数反分析的研究主要集中在正法求解上，正法大体可以分为输入模型、控制原则、反馈模型三部分，基本实现思路如图1所示。

图1 算法实现流程

3.1 正分析模型和目标函数

混凝土热传导问题需要考虑空间和时间积累因素，很难利用数学方法得到解析解，一般只有在特定条件下才能实现，比如:初始温度影响消失、环境温度为常量或线性变化等。大连理工大学的张宇鑫［12］在一维热传导的前提下，根据叠加原理将上述问题分解为四种情况，并通过 Laplace积分变换最终得到了温度场解析解。在研究起步阶段，主要用差分法来分析一维热传导问题。随着有限元理论迅速发展，研究领域逐步扩展到三维瞬态热传导问题，并成为建立正分析模型的主要途径。王一博等［13］基于有限元理论和精细积分法提出了新正演模型，并获得了很好的计算结果。河海大学的朱岳明教授对参数可辨识性［14］进行了论证。

建立正分析模型后，需要借助目标函数对响应值和实测值进行比较，控制识别精度。目标函数的种类可分为如下几种:①最小二乘理论;②Markov链理论;③最大似然估计理论;④Bayesian理论。

3.2 实现方法

3.3 仿生智能及其进化反分析法

随着研究的深入，各国学者从自然界生物行为入手，借鉴它们的运行机制，形成了仿生智能算法，在反分析领域中迅速得到推广应用，目前主要的算法见表1。

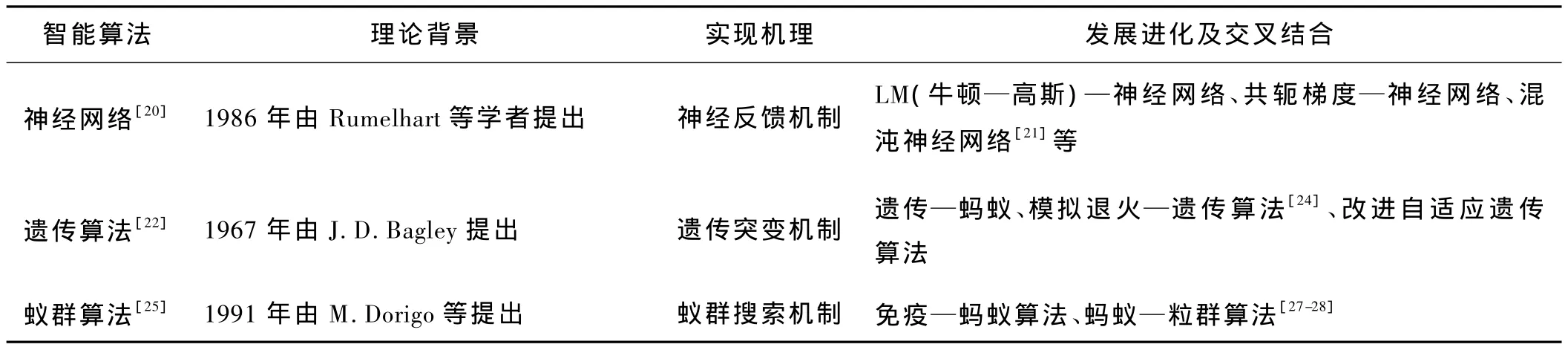
表1 智能算法简介

1)神经网络

神经网络算法［21-22］一般由输入层、隐含层和输出层构成。神经网络三层感知器之间通过神经元进行信息传递和反馈，可以实现任意非线性映射。这使得神经网络算法得到广泛的应用。然而标准的神经网络算法具有收敛速度慢、易形成局部搜索停滞、计算速率难以确定等缺点。现在的神经网络基本都与其他算法相结合，相互借鉴优势形成新的综合优化算法。

2)遗传算法

遗传算法［23，25］的理论基础是达尔文的生物进化理论，它借鉴了生物界中的自然选择和群体遗传机制，通过选择、交叉和变异算子对初始种群进行搜索，根据不同的适应度函数，产生新的种群，并通过遗传操作，一代代地向最优解进化。主要内容包括:编码、产生初始种群、构造适应度函数、选择遗传、突变算子。遗传算法适用于解决复杂的非线性和多维空间寻优问题，它具有优秀的全局搜索能力、平行实现能力、目标函数的普适能力等，使其成为智能算法中应用最广、进化最多的算法。标准的遗传算法还存在着计算速率低、对适应度函数依赖性大、易形成局部过早收敛等问题，进化算法［28］很好地弥补了这方面缺陷。

3)蚁群算法

蚁群算法［26］模拟蚂蚁在觅食时通过留下信息素来影响后面蚂蚁的搜寻路径，实现搜索协调，最终获得最优解。蚁群算法具有自适应性、正反馈计算、并行实现、强鲁棒性、易与其他算法结合等优点，并逐渐形成了基本蚁群算法、自适应蚁群算法、最大最小蚁群算法、基于信息量分布的连续蚁群算法、基于网格划分的连续域蚁群算法等经典类型。现在，蚁群算法已经深入到电力系统优化、交通配流、岩土工程、化工生产等诸多领域，成为国际智能计算领域中备受关注的研究热点和前沿性课题。

热传导反演问题的主旨是通过某些已知的信息，如监测数据、初始条件、边界条件、部分热学参数等，借助反演技术估算或确定热学参数未知量。神经网络和遗传算法的程序复杂，编写难度大，本文根据实际工程需要，选用基于网格划分的连续域蚁群算法编写程序，获得了很好的识别结果。

4 工程算例

本文针对东北的气候特征，在某高速铁路沿线浇筑试验墩，墩身高4.0 m，宽3.8 m，厚2.0 m，选取9 个测点埋设传感器，监测混凝土结构和环境的温度变化情况。采用连续“蚁群”算法对混凝土热学参数进行反演分析，并通过试验墩温度场模拟反馈识别效果。其中，密度、比热容和导热系数可以根据施工配合比通过经验公式计算得到，密度 ρ=2 400 kg/m3，比热容c=0.881 8 kJ/(℃·kg)，导 热 系 数 λ = 9.14 kJ/(m·h·℃);将绝热温升最终值、规律参数a和b、表面放热系数β作为识别项，待定参数变化范围和计算结果如表2所示。利用ANSYS软件模拟瞬态混凝土温度场，将计算温度值和实测温度值进行比较，如图2所示，可以发现计算误差控制在5%之内，具有较好的识别精度，由“蚁群”算法反演得到的热学参数是可靠和有效的。

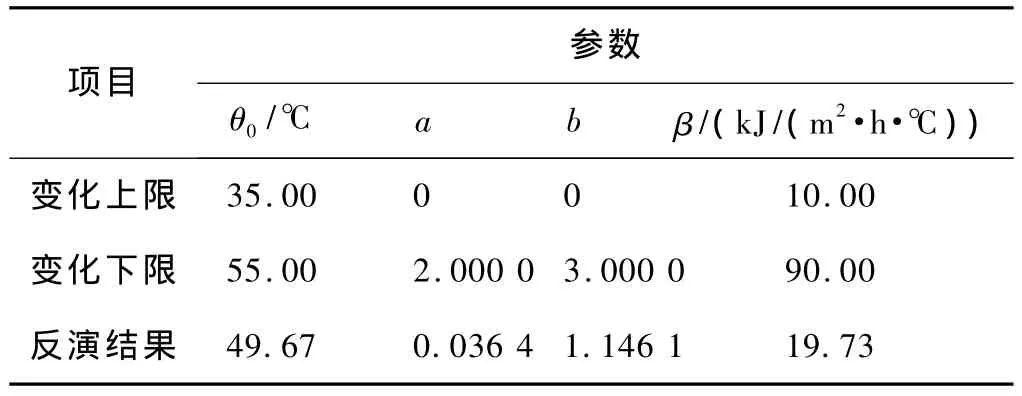
表2 参数变量范围及反演结果

图2 网格化模型和1号，4号，7号测点反演结果对比

5 结论

1)在混凝土热学参数反分析领域中，逆法的应用受到限制，但其本身理论依据简单、计算量小，在特定条件下可以较快得到热学参数。遗传算法和神经网络引入较早，成为应用和进化发展最多的算法，理论体系较为完善，与其他算法结合形成的混合算法在识别速度和识别精度方面有了更大提高。

2)本文将蚁群算法应用于实际工程当中，编译蚁群算法程序，以实测数据为依据获得热学参数，工程实践表明相应测点的反演值和实测值误差大体控制在5%左右，识别结果良好。

3)蚁群算法是一种强鲁棒性算法，只需要小范围改动就可以实现与其他算法的结合，借鉴其他算法的优势，形成更为完善更为有针对性的组合优化算法，是蚁群算法逐步发展的方向。随着研究的深入，蚁群算法将会给我们呈现出一个分布式和网络式的优秀反分析方法，为工程数值分析提供更为广阔的平台。

［1］郝静如，米洁.用蒙特卡洛法计算可靠度的程序优化［J］.机械设计与制造，1998(1):6-8.

［2］何光宇.混凝土温度场反演分析与施工反馈分析［J］.华北水利水电学院学报，2004，25(4):9-13.

［3］赵新铭，张剑，刘宁.大体积混凝土力学参数的 Bayes随机优化反演［J］.土木工程学报，2005，38(10):93-97.

［4］李守巨，刘迎曦，王登刚，等.混凝土重力坝材料参数识别的正则化最小二乘法［J］.计算物理，2000，17(6):702-707.

［5］韩林，张子明，倪志强.应用改进算法的对称逐步超松弛预处理共轭梯度法［J］.河海大学学报，2010，38(3):278-283.

［6］刘迎曦，王登刚.材料物性参数识别的梯度正则化方法［J］.吉林大学自然科学学报，2000，20(2):56-60.

［7］余波，邱洪兴.基于单纯形加速理论混凝土瞬态温度场热学参数的动态反演研究［J］.工业建筑，2007，37(21):374-378.

［8］胡纯德，祝延军，高随祥.基于人工免疫算法和蚁群算法求解旅行商问题［J］.计算力学学报，2004，34(3):60-63.

［9］马军建，董增川，王春霞，等.蚁群算法研究进展［J］.河海大学学报，2008(3):140-143.

［10］朱伯芳.大体积混凝土温度应力与温度控制［M］.北京:中国电力出版社，1999(3):8-17.

［11］黄达海，刘广义，刘光廷.大体积混凝土热学参数反分析新方法［J］.计算力学学报，2003，20(5):574-578.

［12］张宇鑫，宋玉普，王登刚.基于遗传算法的混凝土三维非稳态温度场反分析［J］.计算力学学报，2004，21(3):338-342.

［13］王一博，杨海天，邬瑞锋.基于时域精细积分算法的瞬态传热多宗量反演［J］.应用数学和力学，2005，26(5):513-518.

［14］黎军，朱岳明，何光宇.混凝土温度特性参数反分析及其应用［J］.红水河，2009，22(2):33-37.

［15］张家海，路明，孙书芳.基于变尺度法的前向神经网络混沌学习算法［J］.石油化工高等学校学报，2009(20):54-57.

［16］薛齐文，杨海天，胡国俊.共轭梯度法求解多宗量瞬态热传导反问题［J］.计算物理，2005，22(1):56-60.

［17］陈国荣，李皇胜，李红健.大体积混凝土温度场高速求解方法的改进［J］.河海大学学报，2009，37(4):396-399.

［18］赵新铭，张剑，刘宁.混凝土温度场热学参数反演方法的研究［J］.华北水利水电学院学报，2002，23(4):6-9.

［19］刘宁，张剑，赵新铭.大体积混凝土结构热学参数随机反演方法初探［J］.工程力学学报，2003，20(5):114-120.

［20］韩明.可靠性工程中参数的Bayes估计法及其应用［J］.兵工学报，2009，30(11):1473-1477.

［21］于猛，陈尧隆，梁娟.基于 BP神经网络的碾压混凝土坝温度场反分析［J］.电网与水利发电进展，2008，24(5):59-62.

［22］高春涛.混沌神经网络模型及其应用研究［J］.黑龙江科技信息，2008，33(4):94-96.

［23］常洪江.遗传算法综述［J］.电脑学习，2010，6(3):114-116.

［24］潘长军.模拟退火算法在岩土工程中的研究应用进展［J］.山西建筑，2010，36(16):75-76.

［25］刘学增，周敏.改进的自适应遗传算法及其工程应用［J］.同济大学学报，2009，37(3):303-307.

［26］段海滨.蚁群算法原理及其应用［M］.北京:科学出版社，2005:1-117.

［27］杨燕，靳蕃，KAMEL.微粒群优化算法研究现状及其进展［J］.计算机工程，2004，30(21):3-9.

［28］朱合华，刘学增.基于遗传算法的混合优化反分析及比较研究［J］.岩石力学与工程学报，2003，22(2):197-202.