双基地高频地波雷达海杂波抑制

仇永斌，张 宁，张树春

(1.哈尔滨工业大学电子与信息工程学院，150001哈尔滨，chouyongbin@126.com;2.空军第一飞行学院飞行仿真技术研究所，150001哈尔滨)

无论单基地还是双基地高频地波雷达，海杂波在多普勒谱上都表现为两个明显幅度占优的谱峰，即众所周知的Bragg峰以及Bragg峰之间的连续区，被分别定义为一阶海杂波和二阶海杂波.其产生机理和特性在诸多文献[1－4]中都有详细分析.强功率的海杂波会淹没附近的目标信息，在多普勒谱上形成检测盲区.因而针对海杂波，尤其是一阶海杂波，开发出很多抑制算法.经过实测数据检验有效的算法如奇异值分解法[5－6]、线性预测法[7]、相邻杂波单元杂波对消[8]、杂波预白化法[9]、Root循环对消法[10]等，甚至 Music 子空间算法[11]也能在一定程度上抑制海杂波.这些算法是针对单基地海杂波提出的.单基地海杂波只与雷达工作频率相关，对于平稳的完全发展的海，一阶Bragg峰多普勒频率是缓时变的，在洋流作用下，与理论值会发生偏移，但这种时变特性和偏移特性都不影响把海杂波当作单频信号来模型化.而对于双基地海杂波，不但与雷达工作频率有关，还同杂波单元的双基地角有关，在距离和趋近于基线长度时，海杂波频率具有向零频收敛的特性，同时在双基地角和洋流的作用下，具有明显的展宽效应，在多普勒(RD)谱上，一阶海杂波谱表现为两条收敛的且逐渐展宽的曲线，因而不同于单基地的直线谱形态.这种特性，直接排除了基于线性预测和相邻杂波单元对消等杂波抑制方法应用的可行性.同时，对双基地而言，双基地角很难精确估计，这使得双基地海杂波抑制变得难以实现.Music子空间算法把海杂波当作无方向性的类噪声信号进行处理，可以实现海杂波抑制，也可以用于提取海面洋流信息[12－13].奇异值分解法和Root循环对消算法，单双基地都可以应用，但需要事先检测出海杂波，才能有针对性地抑制杂波.但对于批量处理数据来说，先检测后抑制显然意义不大.对于双基地布局，洋流与地貌状况直接影响杂波谱形态，导致谱峰分裂以及理论值与预测值发生偏差，使得海杂波背景下目标检测变得异常困难，一个直接的影响是杂波会被当作目标被检测和跟踪，形成大量的虚假目标和虚假航迹.针对这一问题，本文根据海杂波谱的先验知识，结合海面的平稳特性，在RD谱上事先确定海杂波频率范围，然后利用Clean算法，在波束形成之前，利用天线阵元的时域数据，把各通道的海杂波抑制掉.这种方法尽管损失了一些出现在杂波频率区域的目标信息，但能够实时处理数据，为后续正常的目标自动检测提供便利.

1 双基地海杂波先验知识

1.1 双基地海杂波谱的影响因素

双基地一阶Bragg峰多普勒频移的理论值为

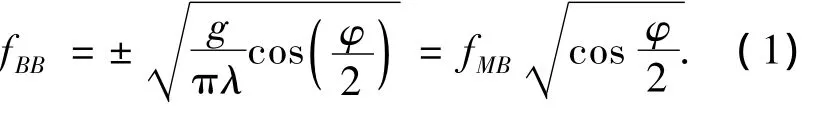
式中:g为重力加速度;λ为雷达工作波长;φ为双基地角;fMB为同频率单基地海杂波多普勒频移.双基地角在杂波单元上是一个变量，因而，在距离和趋近于基线长度的过程中，一阶海杂波谱具有渐进展宽的现象;洋流的作用，不但会加剧这种展宽效应，还会造成杂波频率与理论值发生偏移.图1是一次双基地测量实验的布局，接收天线为8阵元线性阵列，工作频率4.92 MHz.在接收天线阵列法向+35°方向有密集排列的岛屿暗礁.

在岛屿暗礁的方向上进行波束形成，测量的海面回波谱如图2，从图2上可以看到，海杂波展宽现象非常明显，同时，从第30个距离单元开始，谱峰呈现严重的分裂和急遽展宽形态.图3是距离门12上的功率谱，从图3上可以看到，Bragg峰分裂成3个独立谱峰，图3中虚线为Bragg线理论值.这种形态分布在岛屿方向附近，方向波束的RD谱上持续距离长，各距离单元上形态一致，只是谱峰独立程度有所差别，该形态在测量时段内一直是持续的，因而，排除了这种形态有目标和其他杂波的可能.从RD谱上看，具有双基地海杂波特有的曲率特征.因而可以断定，该形态谱峰是由Bragg峰分裂形成.这种形态对杂波检测会遭成严重影响，基于理论预测值以及谱峰形态特征的检测方法无法分辨具有独立谱峰分裂形态且与理论预测值差别较大的海杂波，导致Bragg峰经常被当作目标检测出来.

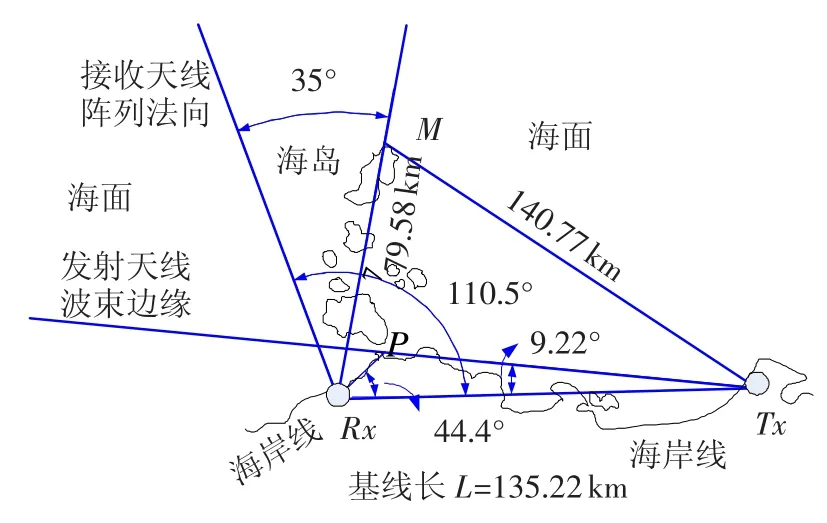
图1 测量实验双基地布局

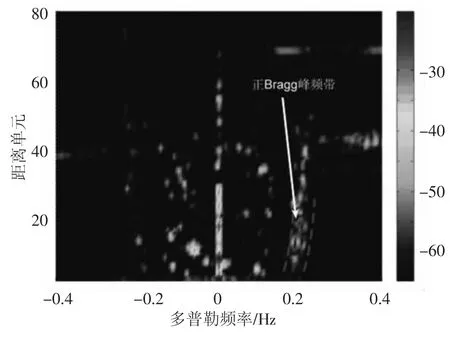
图2 展宽和谱峰分裂的双基地海杂波谱

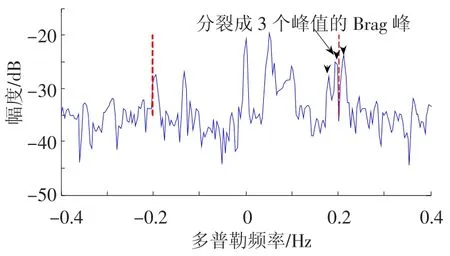
图3 距离门12上的功率谱

图4是另一次实验的结果，波束方向为天线阵列法向+48°(实验布局和工作条件如图5所示)，谱展宽效应表现不明显，但Bragg线的理论值与实测值在近距离门端存在较大偏差，分析表明，该偏差和曲率不一致性是由地貌遮挡以及洋流作用共同产生的.地貌遮挡造成双基地角估计不准确，而真实的双基地角却难以估计;洋流引起的频率偏移也无法准确估计.同时，一个非常明显的特征是:正负Bragg峰向对于理论预测值的偏移量不对称，由于风向的影响，正负Bragg峰谱宽度也不对称.

图4分析表明，双基地海杂波谱峰位置和形态受多重因素影响，利用理论预测值来检测杂波变得非常困难.实际处理结果也表明，海杂波经常被当作目标来检测和跟踪，造成大量的虚假目标，后续的航迹关联变得异常复杂，形成大量虚假航迹.因而，海杂波对正常的目标检测和跟踪造成严重影响，寻求能够实时处理的杂波抑制方法显得非常必要.

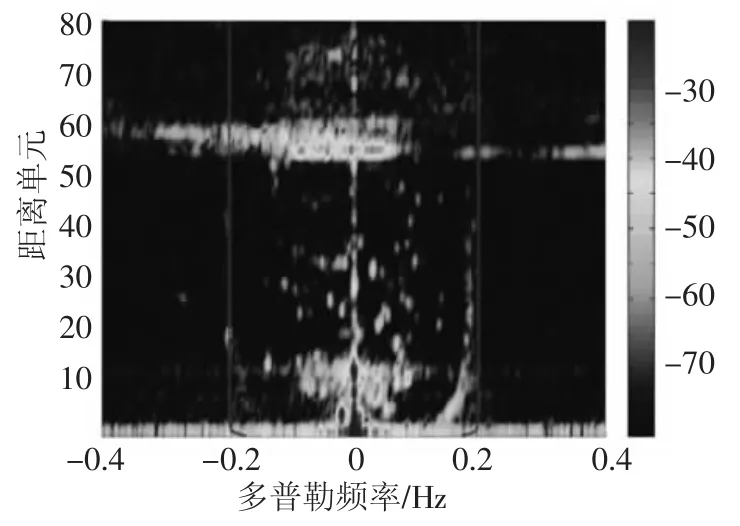
图4 理论值与实测值发生较大偏差的海杂波谱

1.2 双基地海杂波谱分析

对于完全发展的海，海面可以看做平稳的随机过程，海杂波多普勒频移是缓时变的.海态平稳条件下，海杂波谱线位置通常比较固定.海杂波这一特性，可以用来事先在RD谱上确定海杂波的频率范围.该频率范围内，可以全部当做杂波来处理，事实上，对于复杂的双基地杂波谱，即便目标出现在此区域，也很难做出准确的检测.以第2次测量实验为例，说明杂波频率范围的确定方法.

首先分析该实验系统的布局.双基地实验系统的布局示意图如图5所示.

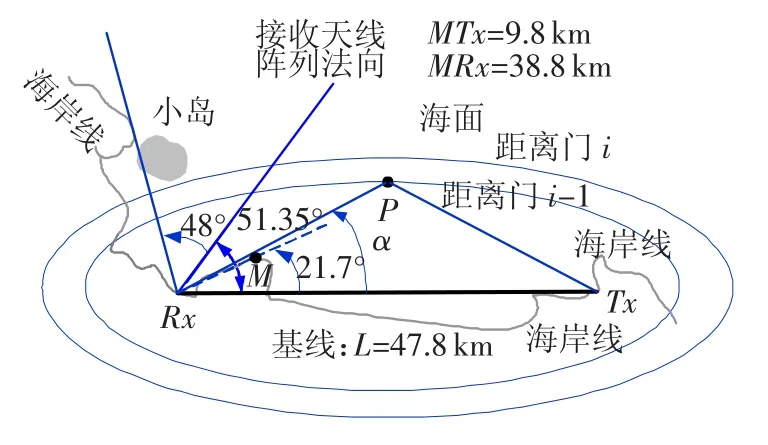
图5 双基地布局和地貌示意图

该系统距离和分辨率为6 km;基线长度为47.76 km;接收天线阵列由8个阵元组成，间距15 m;法向与基线的夹角为51.35°，雷达工作频率3.776 MHz.图5中，机动接收站所处地形复杂，导致理论上是全向的接收天线，由于地物遮挡变得覆盖范围有限，而且波束边界也难以精确定位.

考察图5中接收天线阵列阵元的波束图形，有两条频率线可以确定.第1条频率线是阵元法向所确定的Bragg线，因为阵元法线方向无地物遮挡，因而一定有一阶海杂波谱线与之对应.第2条是各距离单元上的最大双基地角所确定的该单元上的最小一阶海杂波多普勒频移.

考察第i个距离门，该距离门的最大距离和为L+i×ΔR，最小距离和为L+(i－1)×ΔR.设P为距离门内任一点，由图5中三角形TPR可知

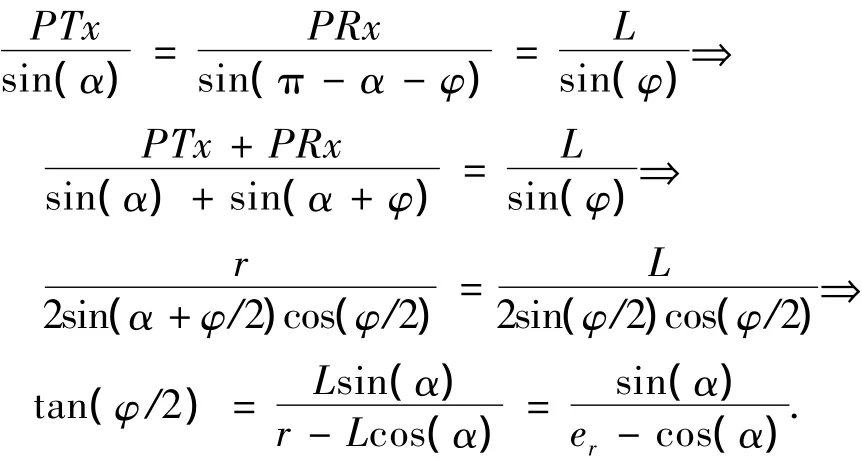
式中:α为PR与基线的夹角;φ为P点对应的双基地角;r为该点对应的椭圆距离和，er=r/L.P点对应的双基地角可写为

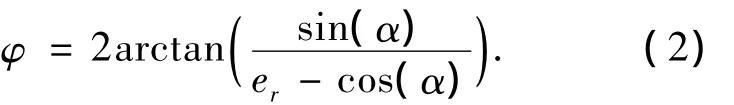
式(2)即为双基地角表达式.当P点位于组成距离单元的最小距离和椭圆与基线垂直平分线的交点时，该点对应的双基地角为该距离门内最大双基地角.无论是利用椭圆的几何图形性质，还是利用双基地角表达式对α求偏导数，并令=0，可求得唯一极值点，都可以得到φ取得最大双基地角时，有

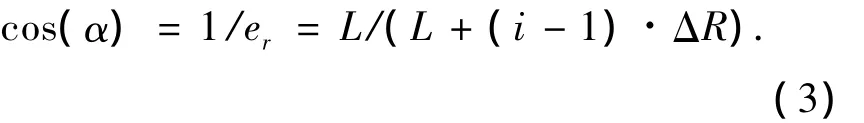
图5中接收天线阵列右侧的地物遮挡，只影响第1个距离门上的最大双基地角，当距离门＞1时，最大双基地角不受地物遮挡影响，是能够唯一确定的，因而能够在一阶杂波谱中找到对应的多普勒频率分量.由式(2)、式(3)可求出对应的双基地角，由式(1)求出对应的Bragg线.

图6给出双基地接收天线阵列阵元1的通道RD谱，数据参数为:相干积累时间为152.99 s;频率分辨率为Δf=0.006 5 Hz;数据长度1 024点.图6中一阶海杂波多普勒频率的内侧边界由最小多普勒频率线平移逼近获得，外侧边界由法线确定的多普勒频率线平移逼近获得.这两条频率线曲率并不一致，利用这一特性，平移这两条谱线，使其在RD谱上逼近一阶海杂波谱的边界.经过平移和目视匹配，如图6中虚线所示，尽量将一阶Bragg峰的频率范围包含到两条虚线之中.由于左右谱峰主瓣有可能不对称，因而平移的尺度可能不同，视具体的测量结果而定.

由于海面是平稳随机过程，在同一次测量过程中，8个阵元的一阶海杂波谱峰都能涵盖在这两条经过平移的频率线之间.图7给出了3 h后的阵元8的RD谱，可以看到，同样的两条频率线，依然涵盖了一阶海杂波谱峰的频率变化范围.因而，这两条频率线所确定的频率范围，可以作为杂波抑制的基准，用于批量处理通道数据.

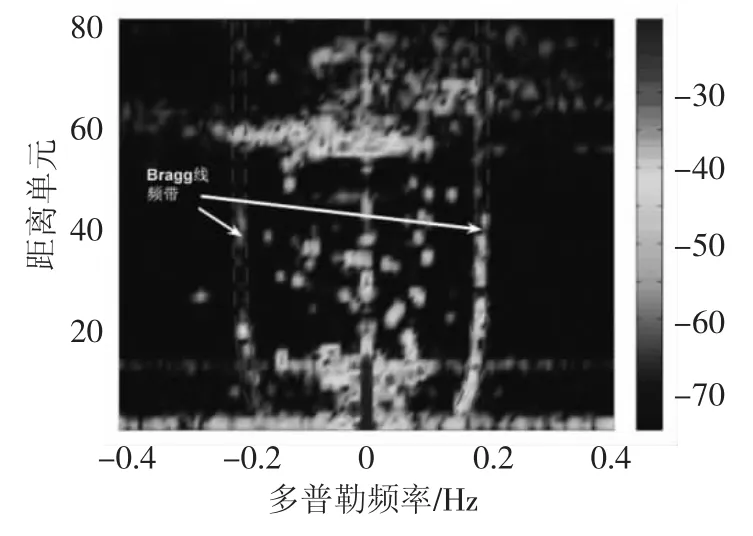
图6 双基地第1阵元RD谱

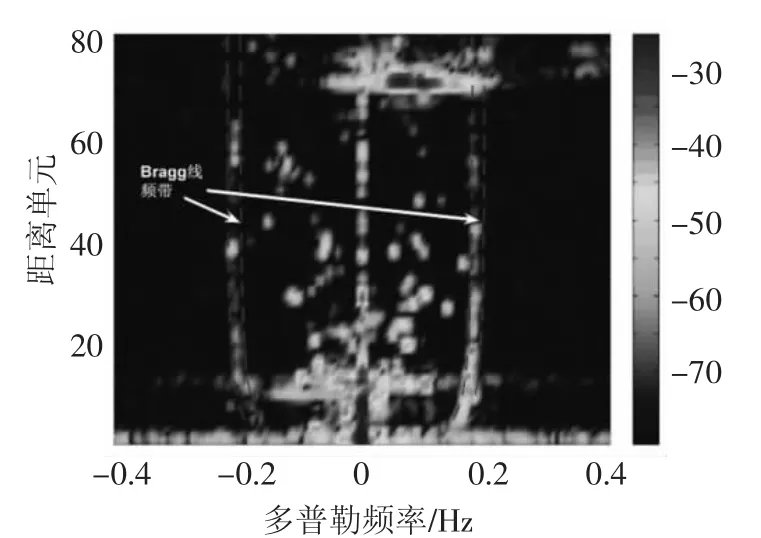
图7 3 h后双基地第8阵元RD谱

对于完全发展的海，实测谱数据研究表明，双基地Bragg线频率随时间是缓变的，围绕均值的波动，因而是一个平稳的随机变量，可以用缓时变频率的正弦信号来模型化.同时，稳定洋流造成Bragg峰位置偏移的范围是可预知的，这一特征，反映到杂波谱随时间尺度的变化特征就是:尽管随时间的推移，Bragg峰频率随时间是变化的，但一阶杂波谱总是在固定的频率范围内出现.同时，在任意时刻，Bragg峰在RD谱上的范围也是固定的.即Bragg峰在该时刻的RD谱上随距离尺度的变化是缓变的，同时范围也是固定的.这两个特性决定了这样一种特征:如果用两条曲线在任意时刻的RD谱上逼近Bragg峰频率的两条边界，并适度留有余量，那么在后续的任何时刻，只要海态保持平稳，雷达工作状态稳定，Bragg峰一定出现在这两根曲线包含的频率范围内.这两根直线确定的频率范围即Bragg线频带.双基地Bragg线频带是恒定的、时不变的.Bragg线恒出现在Bragg线频带内.定义这样一种特征，即Bragg线频带的时不变的特征，为双基地一阶海杂波的平稳性特征.

Bragg线的平稳性特征表明，既然是平稳的随机过程，时间平均可以取代集合平均，任何时段内的统计特征都是集合平均的取样.因而，在测量时段内，只要海态是平稳的，在任意时刻对波束或通道RD谱上对Bragg线频带进行取样，并适度留有余量，都可以做为整个测量时段的Bragg线频带的估计.同时，距离单元内的Bragg峰具有局部幅度占优特征，在功率谱上一般以局部极大值或最大值点形式存在.由于具有谱峰分裂形态，极大值点可能不是唯一的.因而，在谱峰分裂等形态下，只要落入Bragg频带内的极大值点，即可认为是Bragg峰而进行抑制.这些特征即为杂波抑制的基础先验知识.

2 海杂波信号模型和抑制算法

2.1 海杂波信号模型

在实际处理中，单基地一阶海杂波一直被当作复正弦信号来处理.尽管双基地一阶海杂波谱因双基地角影响而形成具有曲率的曲线，并且因距离单元上双基地角的变化而形成谱扩展，但距离门内的谱形态依然表现为两个明显的谱峰，因而一样可以用复正弦信号来模型化，至多因谱峰分裂造成频率分量增加.由上述处理过程知道，事先已经在RD谱上划分出海杂波谱区域，该区域内的杂波分量和疑似杂波的目标分量，都将作为杂波分量被抑制.而出现在杂波谱区域内的非机动目标信号，也一样可以用复正弦信号模型化，因此，假设杂波谱区域内有K个复频率分量(其中包括一阶海杂波分量和疑似杂波信号的目标信号、噪声信号或者电离层杂波信号等)，杂波谱区内的海杂波信号模型可以写为

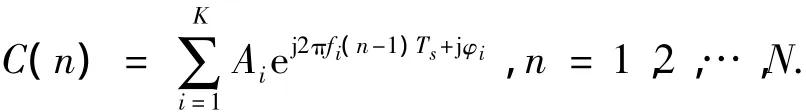
式中:Ai、fi、φi分别为对应信号分量的幅度、频率和初相;Ts为信号采样周期;N为时域信号序列的长度.其中，fmin≤fi≤ fmax，[fmin，fmax]为确定的杂波频率范围.

2.2 海杂波抑制算法

所谓的海杂波抑制，是把位于杂波区域内的能量从整体信号能量中分离出来，而又不改变其他信号的原貌．目的是使杂波能量不被当做目标检测出来，从而实现正常的目标检测，而不是把杂波能量淹没的信号提取出来．

据信号模型，结合海杂波信号具有频率缓时变特性可知，由时域信号序列构造的Hankel矩阵，奇异值分解之后的奇异值能够跟踪窄带缓时变频率的正弦信号分量，因此，基于奇异值分解的Hankel矩阵降秩法能够实现杂波抑制．但该算法计算速度慢，无法实现实时数据处理．

另一种杂波抑制思路，则是基于正弦信号参数估计．如果把信号模型中的正弦信号参数估计出来，在时域信号中将该分量减去，则消除了该信号分量的能量，从而实现杂波抑制．这种正弦信号参数估计的算法很多，比如Clean算法;改进的Clean算法如Relax算法和ROOT循环对消算法;APES(正弦信号幅度相位估计)算法;Capon算法等．后两种算法是超分辨率谱估计算法，对正弦信号参数估计的更精确．Clean算法的优点是速度快，便于实时大批量处理数据．

2.3 Clean算法

Clean算法［14］是一种基于FFT的快速谱估计算法．该算法的要求是:组成信号时域序列的各分量信号的持续时间长度都与进行傅立叶变换处理的长度相同，这一点杂波信号模型无疑是能够满足的．针对复正弦信号分量组成的杂波模型，提取杂波信号能量的计算方法为:

1)对信号的时域序列S(n)作 FFT，得到S(ω)，求取S(ω)落在杂波频率范围内的最大极大值点．该极值点所对应的幅度，相位和频率分别作为第1个分量信号的参数估计，即

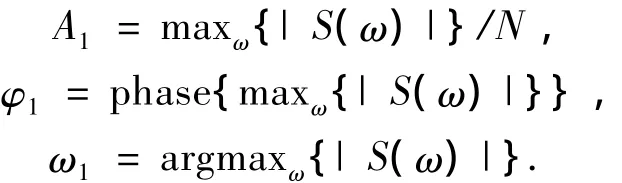
第1个被提取的杂波分量可以写为

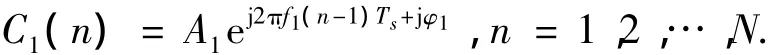
将该分量从原时域序列中减去，提取该分量信号能量，即

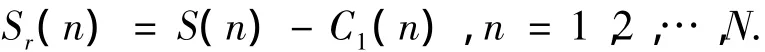
对剩余信号Sr(n)重复上述过程，直到满足收敛条件．这里进行杂波抑制的目的是使杂波区域内的能量不被当做目标检测出来，因而只要杂波区域内的最大极大值点的功率小于平均噪声功率，即可认为杂波抑制完成．而平均噪声功率很容易事先求取．因此，可通过计算杂波区域内最大极大值点的功率来设定收敛条件．

2)如果把相位的估计利用剩余能量最小原则来确定，则Clean算法就变成了ROOT循环对消算法．即在［0，2π］上搜索 φi，使得

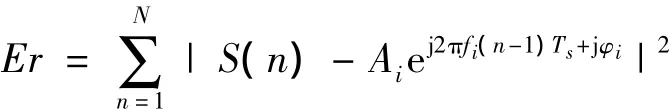
取得最小值［10］．

Clean等谱估计方法用于信号能量提取，一般是从最大值点开始，反复提取剩余能量的最大值信号．但海面回波谱，尤其是通道数据，海杂波一般不是能量最大的信号．实验数据表明，在近距离门端，能量最大信号为地物回波和固定目标回波，造成零频能量最高．其次是航线上的大型舰船目标，海杂波没有表现为能量最强的信号．实际上，风向对海杂波双边谱幅度的影响，也会造成海杂波至少有一侧能量较低，因而，海杂波能量最强的状况并不是普遍现象．这里把Clean算法应用到固定频率范围内，一方面是由于海杂波在功率谱上表现为极值点尖峰，尽管由于谱峰分裂或者其他信号叠加会造成信号分量增加，但既然无从辨别海杂波频率范围内的信号属何种信号类型，不如当作海杂波信号抑制掉;另一方面，这样处理并不违背原算法的信号参数估计准则;再有，杂波频率范围内频率点有限，其中极大值点更少，迭代对消无需几次，即可把杂波能量提取干净，计算速度快，能够实现实时处理．实际处理结果也表明，这样做是可行的．其他谱估计算法，即便是相对较快的ROOT算法，计算速度也远达不到实时处理．

3 杂波抑制处理结果

杂波抑制的处理过程为:首先利用给出的杂波谱特征先验知识，即Bragg线频带在通道RD谱或波束RD谱上的平稳性特征，在RD谱上预先确定Bragg线频带;Bragg峰以极大值点的形式只存在于Bragg线频带内，由于双基地海杂谱中，正负Bragg峰在洋流的作用下发生的谱峰偏移不一定具有对称性，因而只要落入Bragg频带内的极大值点，都将被作为杂波抑制掉．对于频带内的极大值点，利用复正弦信号作为模型，利用Clean算法对模型参数进行估计，之后在信号的时域序列中将该信号模型的估值减去，从而抑制掉频带内所有极大值点对应的频率分量，即提取该分量的信号能量．剩余能量的信号即为杂波抑制后的时域序列．

给出Clean算法得到的杂波抑制结果，这里采用的是波束形成之前的通道数据，在时域完成杂波抑制之后，再进行数字波束形成，得到杂波抑制后波束方向上的RD谱．图8，图9给出了杂波抑制前后16°方向上的RD谱.图9上可以看出杂波能量明显被抑制掉，甚至远低于背景噪声功率，因而不会被当作目标检测出来.图10，图11给出了－32°方向上杂波抑制前后的RD谱.从图形上看，杂波抑制处理效果相当明显，但Bragg频带内的目标信号也同时被抑制掉了，因而损失了这部分信息.

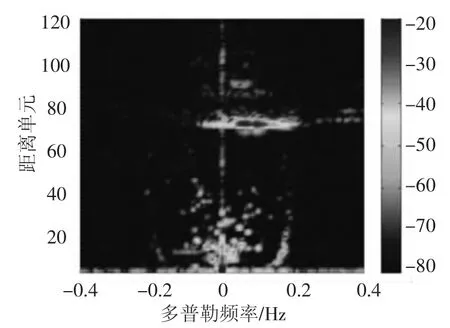
图8 未抑制杂波16°方向RD谱

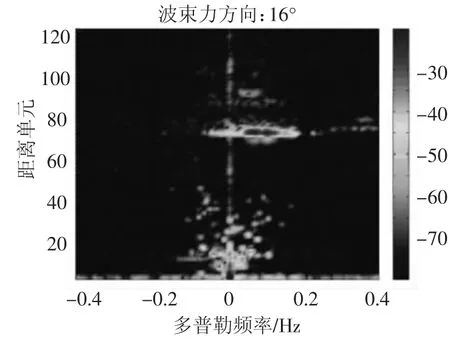
图9 Clean算法处理后16°方向上的RD谱

图10 未抑制杂波－32°方向RD谱

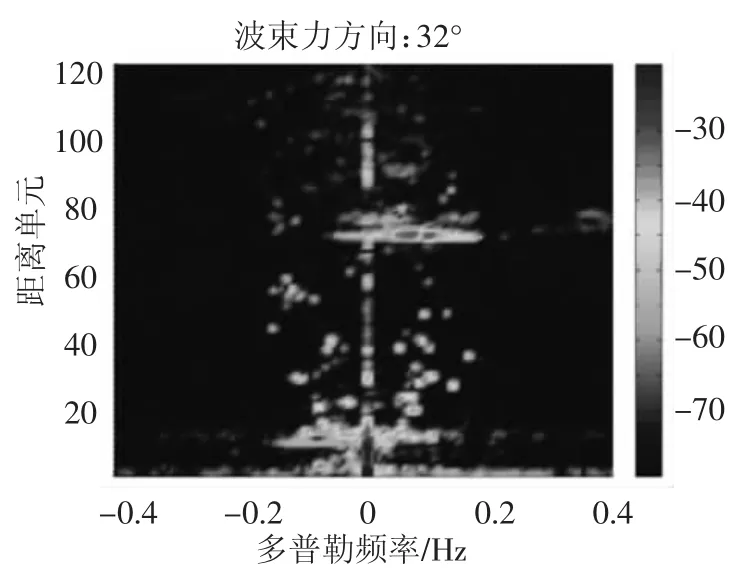
图11 Clean算法处理后－32°方向上的RD谱

作为对比，利用奇异值分解算法进行同样的杂波抑制处理，结果显示，两种方法在处理效果上没有明显差别，但奇异值分解算法有明显的能量残留，因而Clean算法略优于奇异值分解算法.但计算速度上Clean算法远比奇异值分解算法快得多.以处理一个通道120个距离单元的速度对比来说，Clean算法在普通个人PC上运行，只需要不到0.5 s，而奇异值分解算法则需要6 h以上.因而Clean算法可以实现实时处理.

同样的处理方法也可以应用到杂波影响严重的波束方向上，不过需要重新快速的拟合出两条边界曲线.本文所谓的实时，是指在雷达工作开始的一小段时间，可以通过先验知识确定杂波频率范围，之后的处理过程，只要海面是平稳的，可以一直延续下去.

对于Bragg线频带内损失的信号，由于系统是多频同时工作的，多频可以部分解决信号损失的问题.如果大量信号出现在该频带内，则针对该频带内的杂波形态特征进行杂波检测，研究表明，如果杂波分裂，则在相当的角度范围和距离范围内具有同样的形态特征.

4 结论

1)由于双基地海杂波受多重因素影响，比如洋流和岛屿等因素引起谱峰严重展宽和分裂;洋流和地貌等造成杂波频率理论预测值与实测值发生较大偏差.

2)在距离和较小时，杂波谱展宽等，导致杂波背景下的目标检测变得异常困难，因而，从通道数据入手，采用一种类似于强制性“挖除”的方法来抑制海杂波.

3)提出的算法主要实现的是牺牲少量淹没在杂波区内的目标信号，达到正常目标的检测.对双基地来讲，海杂波形成速度谱上的检测盲区，淹没于其中的目标信号本身确实难以检测和分离，无法准确判定是目标信号还是杂波信号.

[1]BARRICK D.First-order theory and analysis of MF/HF/VHF scatter from the sea[J].IEEE Transactions on Antennas and Propagation，1972，20(1):2－10.

[2]TRIZNA D B.A model for the First-order doppler Spectrum for bistatic HF radar surface wave sea scatter[C]//IGARRS 2001.Sydney:Australia，2001:7 －11.

[3]TRIZNA D B.A bistatic HF radar for current mapping and robust ship tracking[C]//OCEANS 2008.Wash-ington，DC:IEEE，2008:1－6.

[4]GILL E，HUANG W，WALSH J.The effect of the bistatic scattering angle on the High-Frequency radar cross sections of the ocean surface[J].Geoscience and Remote Sensing Letters，IEEE，2008，5(2):143 －146.

[5]POON M W Y，KHAN R H，LE-NGOC S.A singular value decomposition(SVD)based method for suppressing ocean clutter in high frequency radar[J].IEEE Transactions on Signal Processing，1993，41(3):1421－1425.

[6]HICKEY K，KHAN RH，WALSH J.Parametric estimation of ocean surface currents with HF radar[J].IEEE Journal of Oceanic Engineering，1995，20(2):139 －144.

[7]KHAN R H.Ocean-clutter model for high-frequency radar[J].IEEE Journal of Oceanic Engineering，1991，16(2):181－188.

[8]Defence R＆D Canada，Raytheon Canada Ltd.Experiments with high frequency surface wave radar and development of a practical ground screen method for HFSWR at cape bonavista[R].Report Number:DRDC-OTTAWA-CR-1999-018;RCL-DND-309;ContractReport(CAN)，1998－11－17.

[9]XIE J，YUAN Y，LIU Y.Super-resolution processing for HF surface wave radar based on Pre-Whitened MUSIC[J].IEEE Journal of Oceanic Engineering，1998，23(4):313－321.

[10]ROOT B.High-frequency over-the-horizon radar ship detection through clutter cancellation:an alternative to high-resolution spectral estimation[C]//Proceedings of Advanced Signal Processing Algorithms，Architectures，and Implementations VII. San Diego， CA:SPIE，1998:488－500.

[11]TONY P，REZA D.System and method for spectral generation in radar:US Patent，6822606[P].2004 －09－16.

[12]Barrick D E，ISAACSON J，LILLEBOE P M，et al.O-cean surface current mapping with bistatic HF radarz:US Patent，6774837[P].2004 －08 －10.

[13]杨绍麟，柯亨玉，侯杰昌，等.OSMAR2000基于MUSIC的超分辨率海洋表面流算法[J].武汉大学学报，2001，47(5):601－608.

[14]邹虹，保铮.多分量线性调频信号的时频分析[D].西安:西安电子科技大学，2001.