自然超空泡航行体弹道稳定性分析

曹 伟，魏英杰，韩万金，王 聪

(1.哈尔滨工业大学航天学院，150001哈尔滨，caowei@hit.edu.cn;2.哈尔滨工业大学能源学院，150001哈尔滨)

航行体在水下高速运动时，周围液体汽化，头部产生充满气体和水蒸气的空腔，空腔向后延伸并覆盖航行体大部分或全部表面，称为超空泡.超空泡的生成能够使航行体的阻力减少90%以上[1].超空泡航行体的外形结构、流体动力特性等与鱼雷等普通水下航行体的区别较大，在弹道仿真研究的编程与仿真分析过程中必须予以重点考虑[2－3].超空泡可以分为自然超空泡和通气超空泡两种，通气超空泡依靠人工通气增加空泡内压强生成超空泡.依靠通气对空化数的调节作用，通气超空泡航行体在航行体速度、深度发生实时变化时，也能够维持空化数的稳定不变.因此在通气超空泡航行体的弹道仿真过程中，可以设定空化数为一固定值，这样其空泡特性就基本保持不变，较容易实现计算程序的迭代收敛和航行体仿真弹道的稳定(当然这一结论是在不考虑通气的不稳定性及通气控制系统的延迟特性等实际情况下得出的).而对于自然超空泡航行体，其空化数随着速度和航行深度的变化而实时变化，空泡形态、滑行力等也随之实时变化.

在弹道仿真程序中，自然超空泡航行体的空化数确定依赖于前一瞬时的速度和深度等航行状态;如果这些航行状态变化较大，那么空泡形态、滑行力等也会随着发生较大变化或较为剧烈的振荡.这一特性增加了航行体弹道的不确定性，同时也给计算程序的迭代收敛带来很大的困难.

本文针对空化数实时变化的自然超空泡航行体的弹道稳定性问题，对前期已经初步完成的弹道仿真程序进行了改进和完善，仿真分析了110 m/s速度下的弹道特性，为进行超空泡航行体的反馈控制研究提供理论基础.

1 超空泡形态描述

根据文献中超空泡鱼雷的外形结构，简化设计了本文的计算模型，如图1所示.弹体最大直径0.533 m，圆盘形空化器，直径0.167 m;尾舵为“十”字形.为了分析空泡覆盖情况，将弹身分成空泡段、部分浸湿段和全沾湿段3部分[4].

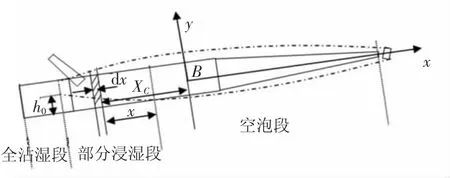
图1 超空泡航行体外形结构及浸湿情况

超空泡的外形近似为椭圆，半径表达式[5]如下:

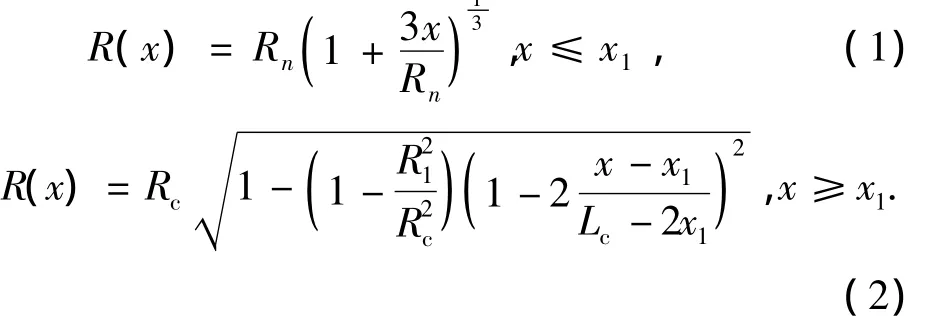
其中:x=x1处称为“一致截面”;Rc为空泡最大截面处的半径;Lc为空泡总长度.Rc和Lc的计算可以用Savchenko[6]提出的经验公式(空化数范围0.012～0.057)获得，即

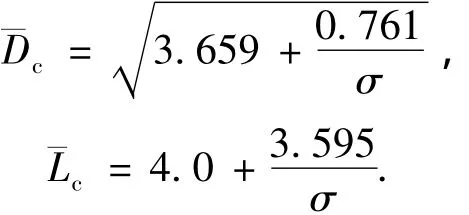
利用上述公式计算出空泡的最大半径和长度，然后代入式(2)，即可计算得到空泡各截面上的空泡尺寸.

2 自然超空泡航行体受力分析和程序编制

超空泡航行体在运动过程中受到的力和力矩主要有:空化器流体动力、弹身流体动力、尾舵流体动力、重力、浮力、推力等(具体分析和公式推导详见参考文献[4]和[7－8]).

关于滑行力的计算是超空泡问题研究的重点，根据Wagner的理论[9]，在图1所示的切片dx内，推导出滑行力表达式如下:

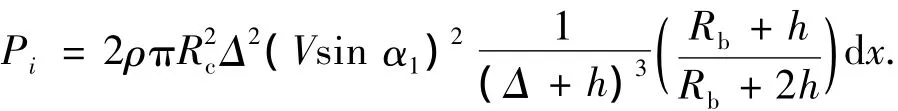
其中:Rc为空泡半径;Rb为弹体半径;h为弹体浸入水中深度;Δ=Rc-Rb;V为航行体速度;α1为空泡中心线和弹体中心线间的夹角.

将整个部分浸湿段划分成若干切片，累和得到滑行力和力矩的表达式[4]如下:

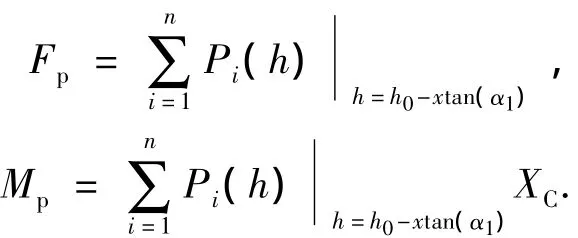
其中h0为部分沾湿段末端的弹体浸湿深度，Xc为切片到雷体系原点的距离.

超空泡航行体纵向运动动力学方程[4]如下:

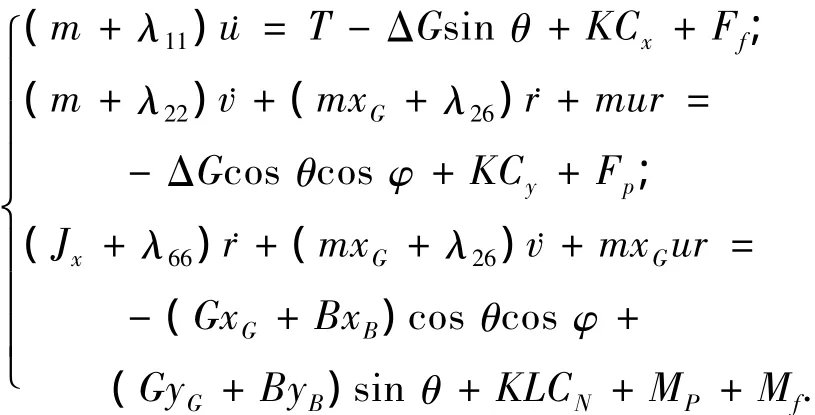
相应的运动学方程如下:

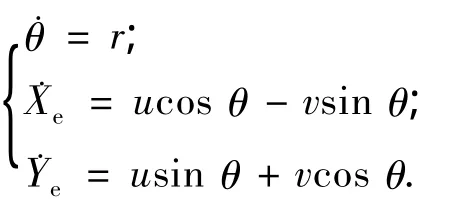
基于超空泡航行体纵向运动方程组，对前期已经初步完成的弹道仿真程序进行了改进和完善，增加了用于计算自然超空泡航行体空化数、操舵优化和后处理等模块.编程过程中忽略了航行过程受到的扰动，并假定航行体受到的推力恒定(与阻力值接近，使航行体的航行速度基本保持不变).

对于自然超空泡航行体，不设定通气规律，而空化数是根据空化器附近的压力、速度值等计算获得的.当程序用于计算通气超空泡问题时，需要对通气规律进行简化设定.

程序利用matlab的m文件编制，微分方程组的求解使用ode45函数.在每一步计算之前，首先利用前一时间步计算获得的速度和深度等航行状态确定新的空化数，然后重新计算空泡形态、空泡与航行体的位置关系、流体动力参数等;最后求解微分方程组，获得当前的航行状态变量.

由于计算过程中各力和力矩都进行了离散化处理，没有像鱼雷控制研究中首先进行平衡攻角和平衡舵角的计算，所以增加了操舵优化模块，利用程序中的迭代分析获得最佳的操舵规律，当航行体稳定直航时，其所处的攻角和舵角状态即是平衡攻角和平衡舵角.

3 仿真结果分析

设计了1个自然超空泡航行体直航弹道算例，以分析空化数实时变化时的受力及弹道特性.本算例中，初始航行体冲角、雷顶舵舵角为零，初始航行速度110 m/s、初始航深10 m、仿真时间4 s.

为了使航行体基本保持定深运动，需要调整雷顶舵舵角，经过操舵优化模块的迭代优化，获得较好的操舵规律如下:初始雷顶舵舵角设为0°，在0.1 s内，按照线性规律操舵至－3.98°，使航行体俯仰角变为0°，这时调整雷顶舵舵角，使其达到平衡舵角－1.68°，航行体基本处于定深直航状态.操舵时序如图2所示，仿真结果如图3～图4.

从图3～图4中可以看出，当经过了两次操舵，航行体基本处于定深直航状态后，航行体所受到的滑行力和滑行力矩处于规律性的振荡中，航行体冲角、俯仰角速度等也类似;而航行体的俯仰角在单调减小的过程中呈现出相同的小幅振荡;航行体垂直方向位移先是小幅上升，然后小幅下降.

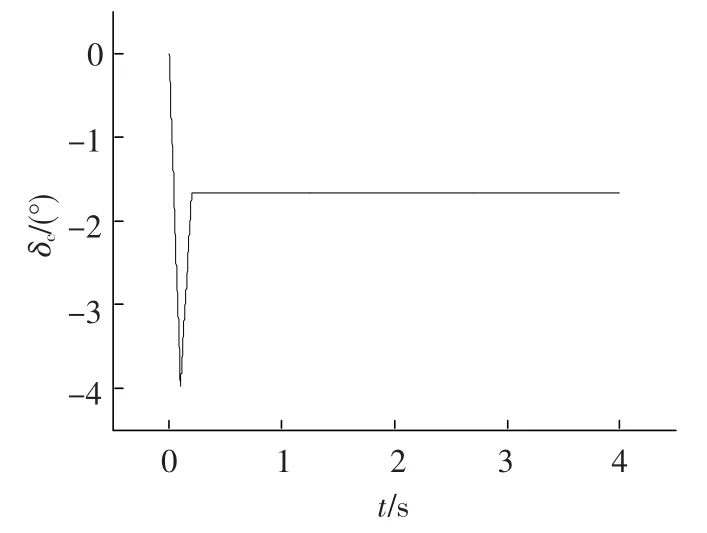
图2 时间－ 雷顶舵舵角曲线

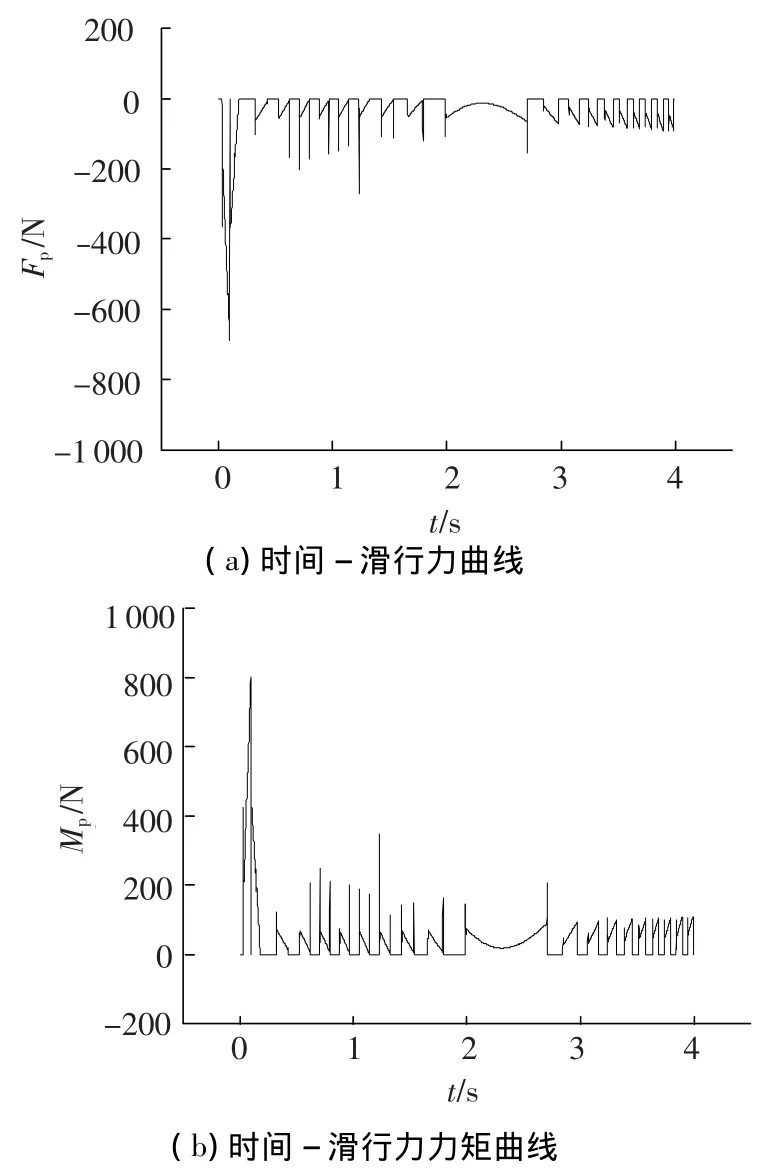
图3 时间－滑行力及力矩曲线(自然超空泡)

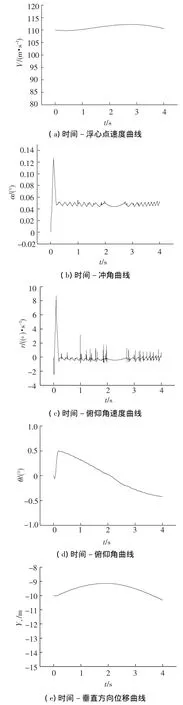
图4 时间－弹道曲线(自然超空泡)

综合各曲线变化规律和超空泡航行体的自身特性，分析得出弹道规律如下:

1)由于航行体没有反馈控制，导致航行深度、航行速度随时间有持续的小幅变化，由此引起空化数的小幅变化(本文以空化数减小为例说明整个变化过程);

2)由于空化数变小，使超空泡的长度和直径增大，由此引起航行体和超空泡的相对位置关系发生变化，航行体尾部突出超空泡之外的区域减少，滑行力减小，使航行体受力失衡;

3)航行体在失衡力系作用下自身运动状态发生变化.随着滑行力减小，航行体所受浮力减小，冲角增大，弹轴与空泡轴线夹角增大;而这一变化又使航行体尾部突出超空泡之外的区域增大，滑行力增大，周而复始，体现出航行体在空泡壁面附近的规律性的振荡特性;每次振荡的幅值与周期不尽相同，既具有一定的重复性，也有积累后发生突变的可能(如仿真第2.0～2.7 s时的情况).

3.3 自然空化与人工通气情况对比分析

为了对比分析是否进行人工通气对航行体受力及弹道特性的影响，设计了相同初始条件和操舵规律的通气超空泡航行体直航弹道算例，通气规律设计见参考文献[10]，巡航段空化数设计值为0.025，仿真结果如图5～图6所示.

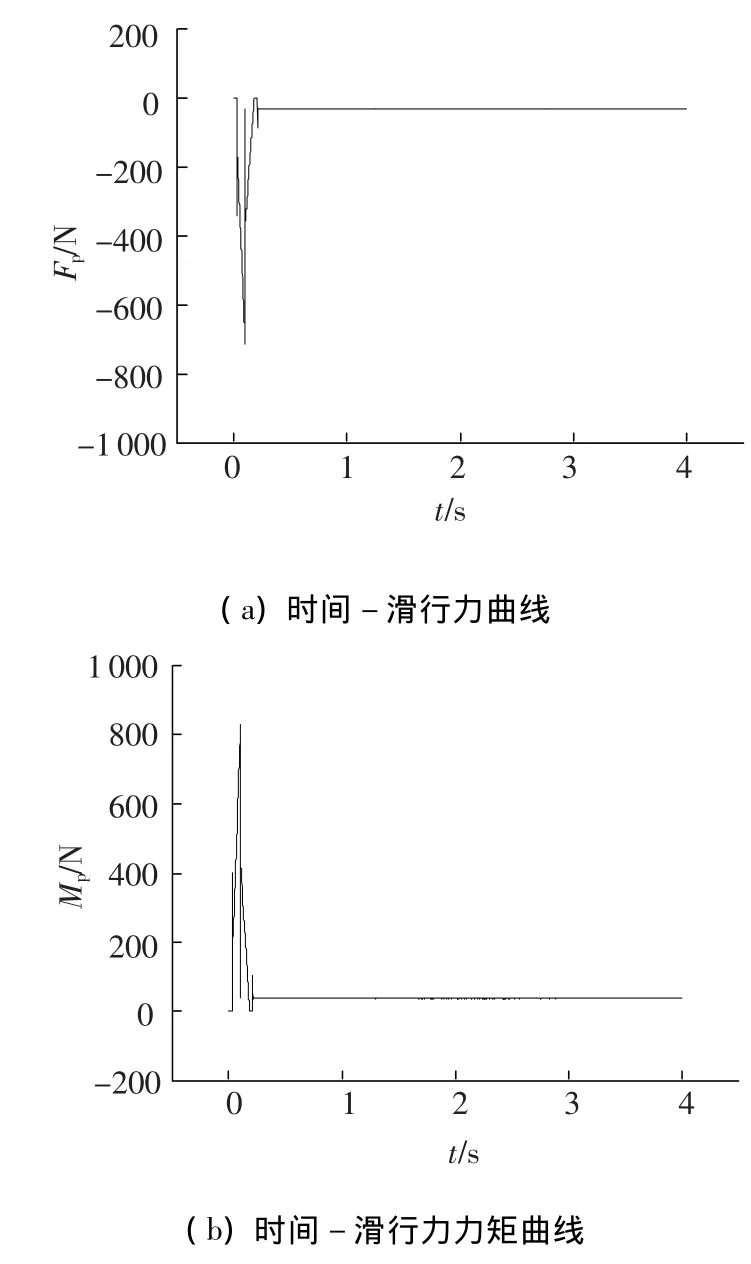
图5 时间－滑行力及力矩曲线(通气超空泡)

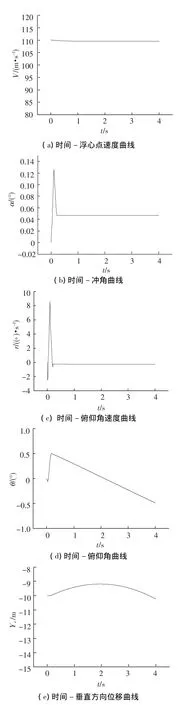
图6 时间－弹道曲线(通气超空泡)

从图5和图6分析可知，对于通气超空泡算例，当操舵过程结束后，因假设空化数受人工通气的调节，不随速度和航行深度实时变化的影响，所以超空泡形态能够保持不变，航行体也能够稳定的在空泡内航行，滑行力维持在1个稳定数值上，各曲线均没有规律性的振荡出现.可见在不考虑通气干扰的情况下，人工通气减小了超空泡航行体的空化数和姿态振荡，比自然超空泡航行体更易维持稳定的航行姿态和整体受力平衡.

4 结论

本文对空化数实时变化的自然超空泡航行体在110 m/s速度下的弹道特性进行了仿真分析，并与人工通气情况进行了对比，得出如下结论:

1)不考虑通气干扰的通气超空泡航行体，较易维持稳定的航行姿态和整体受力平衡;

2)空化数时变的自然超空泡航行体所受到的滑行力和滑行力矩等处于规律性的振荡中，航行体冲角、俯仰角速度等也有类似的振荡变化;

3)对于空化数时变的自然超空泡航行体，由于空化数变化使航行体受力失衡，航行体的姿态与受力互相影响，使航行体在超空泡壁面附近做规律性的振荡.

[1]KUKLINSKI R，HENOCH C，CASTANO J.Experimental study of ventilated cavities on dynamic test model[C]//4th International Symposium on Cavitation.California:CaliforniaInstituteofTechnologyPasadena，2001:20－23.

[2]RUZZENE M，KAMADA R，BOTTASSO C L，et al.Trajectory optimization strategies for supercavitating underwater vehicles[J].Journal of Vibration and Control，2008，14(5):611－644.

[3]冯光，颜开.超空泡航行体水下弹道的数值计算[J].船舶力学，2005，9(2):1－8.

[4]曹伟，魏英杰，韩万金，等.超空泡航行体典型弹道特性仿真研究[J].哈尔滨工程大学学报，2010，31(3):323－328.

[5]VLASENKO Y D.Experimental investigation of supercavitation flow regimes at subsonic and transonic speeds[C]//Proceedings of the 5th Intermational Symposium on Cavitation.Osaka:Hotel Osaka Sunpalace，2003:1－4.

[6]SAVCHENKO Y N.Experimental investigation of supercavitating motion of bodies[C]//VKI Special Course on“Supercavitating Flows”.Brussels，Belgium:RTO －AVT and VKI，2001:1 －24.

[7]KIRSCHNER I N.FINE N E，UHLMAN J S，et al.Numerical modeling of supercavitating flows[C]////VKI Special Course on“Supercavitating Flows”，RTO Lecture series 005.Brussels，Belgium:RTO － AVT and VKI，2001:1 －39.

[8]RAHUL K.Trajectory optimization strategies for supercavitating vehicles[D].Georgia:Georgia Institute of Technology，2005.

[9]ANUKUL G.Robust control of supercavitating vehicles in the presence of a dynamic and uncertain cavity[D].Florida:University of Florida，2005.

[10]曹伟，魏英杰，王聪，等.超空泡航行体加速段通气规律设计[J].哈尔滨工业大学学报，2007，39(12):1938 －1941，1944.