缺失数据插补处理方法的比较研究

庞新生

(北京林业大学经管院，北京 100083)

缺失数据插补处理方法的比较研究

庞新生

(北京林业大学经管院，北京 100083)

文章将抽样调查中由于项目无回答所形成的缺失数据作为研究着眼点，从矩阵运算的角度分析了此类缺失数据带来的危害，在此基础上，对缺失数据插补处理方法的基本问题进行了讨论，分析了各种单一插补方法特点及局限性，并介绍了简单随机抽样、分层随机抽样条件下缺失数据多重插补的抽样推断方法，在此基础上，对常用的单一插补和多重插补方法进行了比较，并对简单随机抽样、分层随机抽样条件下缺失数据单一插补与多重插补方法的效率进行了实证研究与比较。

缺失数据；单一插补；多重插补；分层随机抽样；简单随机抽样

缺失数据是数据分析中无法回避的难题之一，由于缺失数据涉及范围很广泛，给出一个明确的界定是很困难的，但从来源看，既包括实验中的缺失数据，也包括调查中的缺失数据；从性质看，既包含没有搜集到的数据，也包括搜集后遗失（或剔除）的数据。具体到抽样调查中，既包括由于无回答所造成的缺失数据，而且也包括由于回答错误、填报错误和汇总错误等原因所造成的，在数据处理中应该加以调整或剔除的数据。本文主要讨论抽样调查中无回答形成缺失数据，根据无回答产生形式不同可分为单位无回答和项目无回答，针对单位无回答主要采用加权法降低数据缺失带来的危害，对于项目无回答通常采用插补法进行处理，在国外相当多的抽样调查中，对缺失数据进行插补处理是非常普遍的，该处理方法的意义在于比列表删除浪费更少的信息，而且当缺失数据为非随机缺失时，替换缺失数据技术比列表删除更稳健，特别是当数据收集者与数据分析者是不同的个体时，插补法更具优势[1]。

1 插补方法的基本问题

列表删除和成对删除是传统的缺失数据处理方法，列表删除具体做法是：删除观测不完全的变量，针对所有回答项目，采用完全数据统计方法分析，这种方法简便，易于实施，不存在编造的数据，但当缺失数据多的时候，采用列表删除会放弃相当数量的信息，特别是当样本量较小的时候，采用这种方法会使数据量变得更少，可能会导致估计效果变差，特别是当缺失数据为非随机缺失时，估计效果会更差。成对删除把目标变量回答单位都包括进来，这种方法使用了所有有效的变量值，它的缺点是根据缺失数据形式不同，各个变量的样本基础总是不断变化，换句话说，每个变量所依据的样本量可能是不同的。基于插补的缺失数据处理技术是用适当的估计补全缺失数据，这样就允许将标准完全数据分析方法用于分析插补后的数据集。无论是调查数据还是试验数据，在统计处理过程都可以看作数据矩阵，如图一所示，m×n维矩阵中x21、xm2均为缺失数据，用·表示。由于矩阵中存在缺失数据，无法进行矩阵运算。从矩阵运算角度来看，列表删除使得原先m×n维矩阵变为(m-2)×(n-2)维矩阵，存在信息损失。成对删除使得原先m×n维矩阵中行向量间、列向量间的维数不一致，数学意义上的矩阵不复存在，只有采用插补法补全缺失数据后得到的矩阵与原矩阵相比，维数没有发生变化，并且能够实现所有的矩阵运算，从这个意义上来说，插补法要比传统缺失数据处理方法更满足统计分析的要求。

图一 含有缺失值的数据矩阵

插补法为每个缺失值寻找一个或多个尽可能与其相似的插补值。一般的插补模型可以表示为：

1.1 单一插补

单一插补是指采用一定方式，对每个由于无回答造成的缺失值只构造一个合理的替代值，将其插补到原缺失数据的位置上,在替代缺失数据后就构造出一个完整的数据集，对新合成的数据可进行相应的统计分析。根据获取插补值的原理不同，单一插补主要包括均值插补、随机插补、热卡插补、冷卡插补和演绎插补。

1.1.1 均值插补

均值插补包括无条件均值插补与条件均值插补，无条件均值插补是用所有回答单元的均值来代替缺失值。在MCAR的假定下，总体均值的估计量是无偏估计。由于插补值是来自分布中心的数值，扭曲了变量的经验分布，总体方差和协方差被低估了。因此，无条件均值插补适合进行简单描述的研究，而不适合较复杂的需要方差估计的分析。在无条件均值插补中，由于所有的缺失数据均用有回答单元的均值进行插补，得到的是过于集中的经验分布。为了改善这种状况，让插补后的数据更好的反映总体的真实波动，从而得到更加准确的方差估计量，提出了条件均值插补。条件均值插补主要包括分层均值插补、回归插补和BUCK方法。分层均值插补在进行插补之前，对变量Y按照数据中的某一个变量分层，然后在每一层中，用该层有记录单元的均值插补该层的缺失值。在MAR的假定下，如果用于分层的变量和缺失机制中的辅助变量一致，对总体均值的估计是无偏的。回归插补是在单调缺失数据模式下，利用回归的预测值代替缺失值。BUCK方法是将回归插补推广到更一般的无回答数据模式，该方法首先基于回答单元从样本均值和协方差阵估计均值μ和协方差阵∑，然后使用这些估计，对每一种无回答数据模式计算含有无回答的变量关于回答变量的最小二乘线性回归，在此基础上，用回归预测值代替无回答值。在MCAR的假定下，可以通过回答的单元构造出总体均值、总体方差的相合估计，从而得到较好的回归预测值以及较好的方差和协方差估计值。当然，该方法也会对总体的方差和协方差产生低估，但是比起无条件均值插补还是有所改善。

1.1.2 随机插补

除了条件均值插补这种改善分布过于集中的方法外，另外一类插补方法就是在插补值中增加随机成分，就产生了相应于均值的无条件随机插补和条件随机插补。在无条件随机插补中，对于缺失数据不再是采用回答单元的均值进行替代，而是在均值的基础上加上随机项。条件随机插补同条件均值插补一样可以分成两类：分层随机插补和随机回归插补，这两种方法都是在条件均值插补的基础上增加随机项，而后者更是较为常见。在随机回归插补法中，插补值可以表示为：

1.1.3 热卡插补

热卡插补是从每一个缺失数据的估计分布抽取插补值替代缺失值，使用回答单元的抽样分布作为抽取分布是最常见的方法。从回答单元中产生插补值所采用的抽样方式决定了在热卡插补下有关总体参数估计量的性质。根据获取插补值的方法不同，热卡插补包括随机抽样热卡插补、分层热卡插补、最近距离热卡插补和序贯热卡插补。①随机抽样热卡插补。在缺失机制是MCAR的情况下，采用该方法得到的插补结果的均值是总体均值的无偏估计，但是会高估方差，并且这个高估的量是不可忽略的。为了改进被高估的方差，可以采用无放回简单随机抽样、限制对回答单元的使用次数、对回答单元进行排序并进行系统抽样的方法等。

②分层热卡插补。在上面提到的热卡插补法中，不论是采用有放回还是无放回的简单随机抽样，所利用的信息仅仅是变量Y自身的数据，没有借助调查中其他完全回答辅助信息，而分层热卡插补则借助了辅助信息，同条件均值插补中一样，首先按照某些辅助变量对变量Y进行分层，然后对分层后的数据进行上述各种热卡插补。

③最近距离热卡插补。利用辅助变量，定义一个测量单元间距离的函数，在变量Y的无回答单元临近的回答单元中，选择满足所设定的距离条件的辅助变量中的单元所对应的变量Y的回答单元作为插补值。距离函数插补法将分层热卡法中的辅助变量从品质型数据扩展到了数值型数据，使得热卡方法的应用进一步拓展。但是，和前面的几种方法相比，该方法由于使用较为复杂的距离函数，使得很难对在这种插补方法下得到的均值和方差等估计量的性质进行考察。

④序贯热卡插补。该方法是在最近距离热卡插补法的基础上提出的。首先对数据进行分层，在每层中按照选定的某一个辅助变量排序，并在其前后相邻的10个数据中，找到使得设定的某一个距离函数的值达到最小的单元，那么该单元所对应的变量Y的回答单元即插补值。这种方法通常要求用于构建距离函数的变量和变量Y之间高度相关。一般情况下，也可以采用其他的变量，但是要求距离函数值的大小和通过该函数所确定的变量Y中的回答单元被选做插补值的次数成正比。

热卡插补法是在实践中最为常用，也是研究最为广泛的一种单一插补方法。同均值插补和回归插补相比较，热卡插补法在保持变量的经验分布方面有比较好的效果。但是，除了随机抽样热卡法外，其他的方法都无法给出明确的均方误差估计公式，这就使得无法对热卡插补法的效果进行理论上的探讨。

1.1.4 冷卡插补

冷卡插补强调插补值是从以前的调查中或其他信息来源中获得的，如历史数据。有关这种方法的理论很少，而且与前面介绍的插补方法一样，冷卡插补同样不能保证消除估计偏差。冷卡插补法中有一种特别的插补方法，即完全匹配插补法。在这种插补法中，替代值和无回答值是相同的测度，但是替代值是来自该单元某些外部的记录。通常的方法则是通过一些唯一确定无回答单元身份的变量，例如身份证号、汽车驾驶证号等，在已有的外部资料中寻找与无回答变量相匹配的值进行插补。

1.1.5 演绎插补

演绎插补主要是通过辅助资料的演绎，找出插补值，也是一种使用辅助变量的插补法，简单的用公式表示就是yi=f(xi)。该辅助资料可以来自本次调查，也可以来自其他的调查或资料。同前面的各种插补方法不同的是，在不考虑变量Y的任何计量误差情况下，这种插补方法是完全确定性的；并且，这种方法的效率很大程度上取决于辅助资料的充分与否。

2 多重插补

多重插补是单一插补的基础上衍生来的，由Rubin在1977年首先提出，是指给每个缺失值都构造一个以上的替代值，这样就产生了若干个完全数据集，对每个完全数据集分别使用相同的方法处理，得到若干个处理结果，最后再综合这些处理结果，最终得到目标变量的估计。

通常讨论插补方法时，往往假定抽样机制是可以忽略的，或者说，目前绝大多数讨论主要集中在简单随机抽样下的多重插补，但在实际调查过程中，允许有多种抽样方法，本文主要就简单随机抽样、分层随机抽样条件下的插补方法做简单地探讨。由于多重插补处理缺失的过程较单一插补复杂，文中仅列出多重插补估计量及方差公式。

2.1 简单随机抽样下多重插补推断

简单随机抽样条件下，在对总体均值Yˉ进行推断时，假设n个单位中仅有nobs个单位回答，采用多重插补处理无回答，n-nobs个缺失单位的每一个都有m个插补值，由此建立m套完整数据集及m个均值和方差l=1，…，m)。根据Rubin重复插补理论[1]可知总体均值Yˉ的多重插补估计是：

总体均值Yˉ的多重插补估计的方差为：

2.2 分层随机抽样下多重插补推断

2.3 单一插补与多重插补的比较

由于插补技术是一种非常重要的缺失数据处理方法，因此，在对各种插补方法进行比较时，需要注意几个原则：第一，插补必须是建立在缺失数据的预测分布基础之上；第二，在考虑插补时，完全回答变量必须考虑在内；第三，插补必须基于需要插补变量的辅助信息；第四，超越数据取值过分的外推是要避免的；第五，为保持完全数据集的分布，插补值必须从预测分布中抽取；第六、必须提供一种把插补值考虑在内的抽样估计误差计算方法。均值插补是唯一一种不满足任何原则的方法，对于所有缺失数据采用唯一的插补值。回归插补和基于EM算法的多重插补满足其中的两个原则；随机回归插补和基于DA算法的多重插补满足四条原则，在四原则的基础上，随机回归插补和基于DA算法看起来最有发展前景，其次是回归插补、基于EM算法的多重插补，最差的是均值插补，具体比较见表1。

表1 插补方法比较[5]

3 缺失数据插补处理方法实例比较

3.1 简单随机抽样条件下缺失数据插补处理方法实例比较

下面通过实际例子来说明简单随机抽样条件下缺失数据插补处理方法之间效率。资料来源于一项关于某城市一周内每个家庭收到广告份数的抽样调查（其中N=2000，n=20，Xˉ=25），如表2所示。通过分析，可以看出两个变量之间存在较强的正相关，即每周每个家庭收到的邮件总数越多，所收到的广告份数也越多。如果广告份数y为目标变量，邮件总数x可作为辅助变量。将原有数据作为完整数据集，按照简单随机抽样方式从中随机抽取5个数据作为缺失数据，见表2括号中的值为假定缺失值。

表2 某城市一周内每个家庭收到广告份数的抽样调查

(1)采用多重插补处理缺失数据

根据Rubin和Schenker的研究显示，在项目无回答率中等程度的情况下，对于研究变量，有2-3组替代值就可以满足估计的需要。因此，可以根据最简单的模型--最近距离法[2]为每个缺失数据插补三次（见表3），估计可以在此基础上展开。

表3 插补后的数据集

如果采用比率估计，对于第一个数据集数据而言，有

方差估计量的估计为

(2)采用单一插补处理缺失数据

为了方便，后续分析中仅就常用的单一插补方法---均值插补、均值插补进行讨论。

①均值插补。目标变量中的缺失数据均使用完全数据集的均值进行插补，结果如表4所示。

采用比率估计，有

②回归插补。目标变量中的缺失数据均使用根据完全数据集建立的回归模型预测值进行插补，结果如表5所示。

采用比率估计，有

估计量方差的估计为

表4 均值插补后的数据集

表5 存在缺失值的数据集

比较计算结果可以发现，在简单随机抽样条件下，当数据缺失不严重时，如果不考虑由于单一插补方法不同所导致偏差的差异，粗略地计算设计效应(deff)，可以发现回归插补的效果要优于均值插补。如果将完全数据估计结果作为真值，如果能充分利用辅助信息，回归插补的结果并不比多重插补差，且多重插补计算较为繁琐，但需要注意的是，无论是回归插补还是均值插补都没有体现缺失数据的不确定性，同时单一插补无法给出偏差的计量方法，因此不能直接根据设计效应判断优劣。

3.2 分层随机抽样下缺失数据插补处理方法实例比较

下面通过实际例子来说明分层随机抽样条件下缺失数据插补处理方法之间效率。资料来源于一项关于居民购买彩票花费的抽样调查(N=844,n1=n2=n3=10,)[4]。将原有数据作为完整数据集，按照简单随机抽样方式从每层中各抽取2个数据作为缺失数据(见表6)，括号中为真值。

表6 存在缺失值的数据集

由表6可得表7中数据，根据分层随机抽样一般原理可得到总体均值简单估计。该小区居民户购买彩票的平均支出估计为：

(1)采用多重插补处理缺失数据

表7 抽样推断中的过程数据

根据Rubin和Schenker的研究显示，在项目无回答率中等程度情况下，对于研究变量，有2—3组替代值就可以满足估计的需要。因此，可以根据最简单的模型—最近距离法为每个缺失值插补2次(见表8)，估计在此基础上展开。

表8 插补后的数据集

表9 插补后的计算数据

将表9数据代入式(5)、(6)，可得总体均值的估计为：

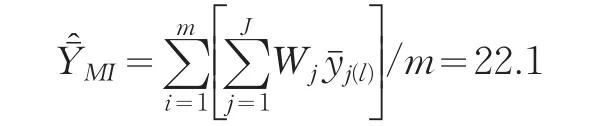
总体均值估计的方差估计为：

(2)采用单一插补处理缺失数据

考虑到易用性，采用单一插补方法处理缺失数据时，本文主要运用均值插补、热卡插补构造完全数据集。

①均值插补。采用目标变量每层内完全数据的均值补全缺失值(见表10)，估计在此基础上展开。

表10 插补后的数据集

表11 抽样推断中的过程数据

因此，估计该小区居民户购买彩票的平均支出为：

②热卡插补。采用现有调查数据补全缺失值(见表12)，估计在此基础上展开。

表12 插补后的数据集

表13 抽样推断中的过程数据

估计该小区居民户购买彩票的平均支出为：

比较计算结果可以发现，在分层随机抽样条件下，当数据缺失不严重时，如果不考虑由于单一插补方法不同所导致偏差的差异，粗略地计算设计效应(deff)，可以发现均值插补的效果要优于热卡插补。如果将完全数据估计结果作为真值，单一插补的结果并不比多重插补差，且多重插补计算较为繁琐，但需要注意的是，无论是均值插补还是热卡插补都无法体现缺失数据的不确定性，同时单一插补无法给出偏差的计量方法，因此不能直接根据设计效应判断优劣。

通过实例比较可以看出，当数据缺失不严重时，无论是在简单随机抽样还是在分层随机抽样情况下，单一插补并不比多重插补差，但多重插补弥补了单一插补法的缺陷，多重插补过程产生多个中间插补值，可以利用插补值之间的变异反映无回答的不确定性，同时，多重插补能给出衡量估计结果不确定性的大量信息，单一插补给出的估计结果则较为简单。与单一插补相比，多重插补唯一的缺点是需要做大量的工作来创建插补集并进行结果分析，因为它主要是执行若干次相同的任务，而非一次，然而数据分析中大量工作在今天的计算环境下是比较容易实现的。

[1][美]Donald.B.Rubin.Multiple Imputation For Nonresponse In Surveys[M]，New York:John Wiley&Sons Inc.1987.

[2][美]Roderick J.A.Little,Donald B.Rubin.Statistical Analysis with Missing Data[M]，New York:John Wiley&Sons Inc.2002.

[3]L.Kish著，倪加勋主译.抽样调查[M].北京：中国统计出版社,1997.

[4]金勇进等编著.抽样技术[M].北京：中国统计出版社，2008.

[5]庞新生.缺失数据处理方法的比较[J].统计与决策,2010,(24).

O212

A

1002-6487（2012）24-0018-05

教育部人文社会科学研究青年基金项目（09YJC910002）；中央高校基本科研业务费专项资金资助（RW2010-4）

庞新生（1970-）,男，山西榆次人，博士，副教授，研究方向：抽样技术和数据分析。

（责任编辑/易永生）