基于夏比试验确定船用钢板断裂韧性

黄 一，陈景杰，刘 刚

(大连理工大学船舶学院，116024辽宁大连，chenjingjiedlut@163.com)

断裂韧性是材料固有的特性，是描述含裂纹损伤结构是否处于安全状态的基础.众所周知，当裂纹尖端的应力强度因子值大于材料的断裂韧性时，裂纹将发生失稳扩展而导致结构断裂.因此，评估含裂纹损伤船体结构的安全状态时，需要确定船用钢板的断裂韧性值.船用钢板通常采用普通强度钢和高强度钢两种.这两种钢板按质量分为4个等级［1］，对于同一强度不同质量等级的钢材，其强度性能相同，仅是材料的断裂韧性不同.因此，确定船用钢板的断裂韧性时，需要研究不同强度不同质量等级对应的断裂韧性值.目前“金属材料平面应变断裂韧性KIC试验方法”［2］被认为是测量材料断裂韧性值精度最高的方法，已作为标准准则在实验中应用.但是该方法存在试验尺寸大、周期长、费用高等缺点，用它评定工程材料的断裂韧性十分困难.因此，长期以来，众学者试图寻找一种能够满意的工程精度的简便方法，通过简单的试验，即可估计出材料的断裂韧性值，其中研究最多的是夏比V型缺口冲击试验［3］，其试验示意图如图1所示，即用规定高度的摆锤对处于简支状态的V型缺口试验片进行一次性冲击，测量试验片折断时的冲击吸收功.

由于夏比V型缺口冲击试验方法费用低廉、速度较快等优点，尽管其冲击特性值的力学意义不明确，船用钢板的抗断裂能力仍旧采用冲击试验吸收能描述.因此，为了获得船用钢板的断裂韧性值，需要建立材料吸收能和断裂韧性二者之间对应关系.国内外学者针对各自所研究的金属材料已提出多种吸收能与断裂韧性二者之间的函数关系［4-7］.然而，这些函数关系由于各自的局限性，无法推广到船用钢板等其他材料.

图1 夏比Ⅴ型缺口冲击试验示意

本文根据日本造船研究会和日本焊接协会所确定的规范，利用矢导浩［8-9］给出的试验数据，由船用钢板吸收能计算出大量不同板厚和使用温度下船用钢板对应的断裂韧性值，进而拟合出材料断裂韧性与钢板厚度和使用温度之间的函数关系，为含裂纹构件安全状态的评估提供依据.

1 基于冲击试验吸收能确定船用钢板断裂韧性

图2和图3是日本三菱重工技术部长崎研究所的矢岛浩教授针对不同质量等级的普通强度和高强度的船用钢板所做的夏比V型缺口冲击试验数据.试验材料及试验温度如表1所示.

表1 试验材料的类型及温度

图2和图3中纵坐标表示夏比Ⅴ型缺口摆锤冲击试验吸收能的测量值，横坐标表示不同材料各自的试验温度与相应的韧脆转变温度的差值.采用这样的横坐标，能够消除不同型号钢板在夏比Ⅴ型缺口摆锤冲击试验中的差异，使试验结果服从公式(1)所示的分布规律［10］.

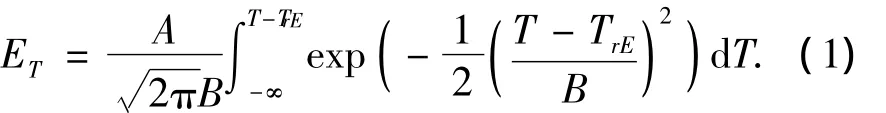
式中:A、B是两个常数;T是试验温度;TrE是50%冲击吸收能转变温度，记为韧脆转变温度;ET是冲击试验吸收能.

图2 基体金属的试验数据

图3 焊缝金属的试验数据

基于上述试验数据和矢导浩教授所介绍的确定材料断裂韧性的方法［8］，实现了由冲击试验吸收能确定船用钢板断裂韧性值的方法，如图4所示.

图4 材料断裂韧性评价的基本过程

图4涉及公式如下:

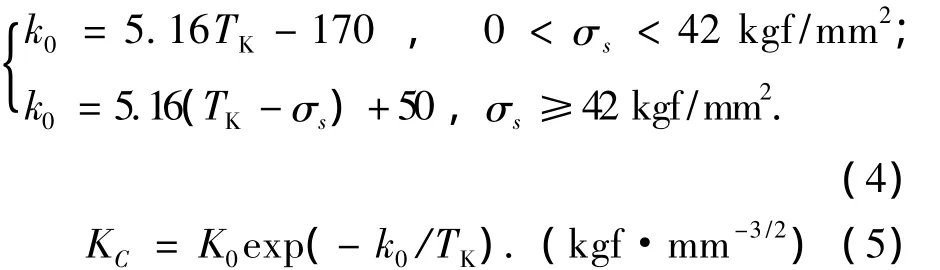
式中:Trs是50%脆性断面率转变温度，记为脆断转变温度，℃;TK是日本造船界评价船用钢板断裂韧性方法中钢板断裂时对应的温度，K;t是钢板厚度;σs是屈服极限;k0和K0为常数.

ΔTrs的取值如下:ΔTrs=25(手工电弧焊、低碳钢)，ΔTrs=40(埋弧焊、低碳钢)，ΔTrs=30(手工电弧焊、高强度钢)，ΔTrs=55(埋弧焊、高强度钢).

从图4可以看出，根据已有试验数据确定钢板的断裂韧性值，首先必须正确确定公式(1)中A、B值.采用最小二乘法原理，在保证图5给定的拟合曲线与试验数据之间方差最小的条件下，获得公式(1)中A、B值.

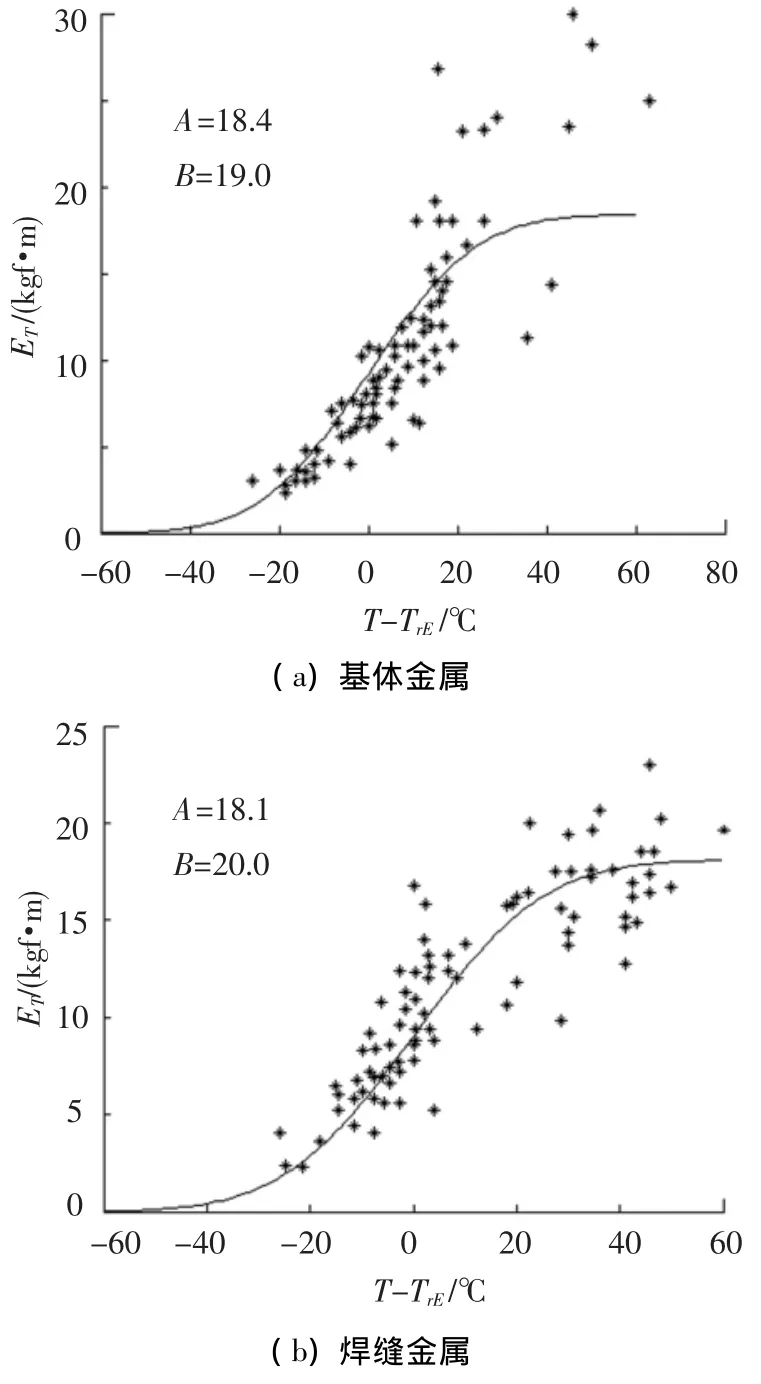
图5 基于不同试验数据的拟合曲线

然后代入公式(5)中的KIC0值.KIC0表示钢板在TK温度下所对应的断裂韧性值.它是根据日本造船界以图6所示的船用钢板进行断裂韧性值测量试验［1］获得的.该试验的基本方法是:保持外加载荷不变，逐渐降低试验温度而使钢板断裂.由于试验模型近似为无限大板，因此可以确定钢板的断裂韧性为

由于拟合曲线的正确与否直接决定着船用钢板断裂韧性计算结果的可信程度.因此，将NK规范中给定的最小吸收能和对应的试验温度，代入图5所示的拟合曲线中，确定不同强度不同质量等级钢板的韧脆转变温度，并与规范中相应结果进行比较来验证拟合曲线的正确性.表2仅给出基体金属中TrE的计算结果及其比较情况，充分说明图5中的拟合曲线是正确可靠的.

图6 日本造船界确定船用钢板断裂韧性的试验模型

表2 不同船用钢板的韧脆转变温度

2 船用钢板的断裂韧性

根据上述由夏比V型缺口冲击试验吸收能计算材料断裂韧性的方法(见图4)，针对不同使用温度(T=0～-50℃)和钢板厚度(t=10～50 mm)，对船用钢板的断裂韧性进行计算，得到大量船用钢板的断裂韧性值.本文仅列出E级高强度钢的断裂韧性值，结果见表3.

由表3可知，在给定的平板厚度下，船用钢板的断裂韧性与其使用温度呈线性关系;在给定的使用温度下，船用钢板的断裂韧性与其板厚呈近似的线性关系.

为了形象地阐述断裂韧性与使用温度和钢板厚度之间的对应关系，根据表3中的数据，利用MATLAB绘制了三者之间的曲面关系，如图7所示，可用平面来代替图7中的曲面.

根据最小二乘法原理，采用多元一次平面拟合技术，可以得到如式(6)所示的断裂韧性KIC与使用温度T、钢板厚度t的函数关系:

对于基体金属和焊缝金属中其他不同强度不同质量等级的船用钢板，其断裂韧性具有相似的分布规律，能够得到与式(6)相似的表达式.

表3 基体金属中E级高强度钢的断裂韧性kgf·mm-3/2

图7 E级高强度钢断裂韧性值的分布

3 不同可靠度下船用钢板断裂韧性

由于图2和图3中的试验数据(ET与T-TrE)存在较大分散性，使上述方法确定的断裂韧性不可避免地存在较大分散性.因此，根据P-S-N曲线的思想，引入可靠度概念，根据试验数据分别确定出不同可靠度下船用钢板的韧脆转变温度及其对应的断裂韧性.

图5中的拟合曲线具有50%的可靠度，拟合曲线上任意点的纵坐标表示在确定的T-TrE下多次冲击试验吸收能的平均值.根据P-S-N曲线思想确定不同可靠度的拟合曲线时，需要获得任意确定的T-TrE下多次冲击试验吸收能其对数正态分布的特征值——均方差.然而，由于在任意确定的T-TrE下实施的冲击试验的试验数据总量不足，如果直接根据各试验温度下冲击试验吸收能的均值和方差来确定不同可靠度下ET与T-TrE之间对应曲线，这样拟合的效果会因数据少而很不理想.因此，本研究以整体试验数据为基础，根据可靠度原理，通过式(7)，模拟出60%、70%、80%、84.1%、90%和95%不同可靠度下基体金属和焊缝金属相对应的整体样本数据.

式中:ETp是p可靠度下吸收能值;ET是吸收能的平均值;σ是吸收能的均方差;up是p可靠度下正态分布值.

对于基体金属和焊缝金属不同可靠度的整体样本数据，采用确定图5中拟合曲线的方法，得到如图8所示的不同可靠度下ET与T-TrE之间的对应曲线.

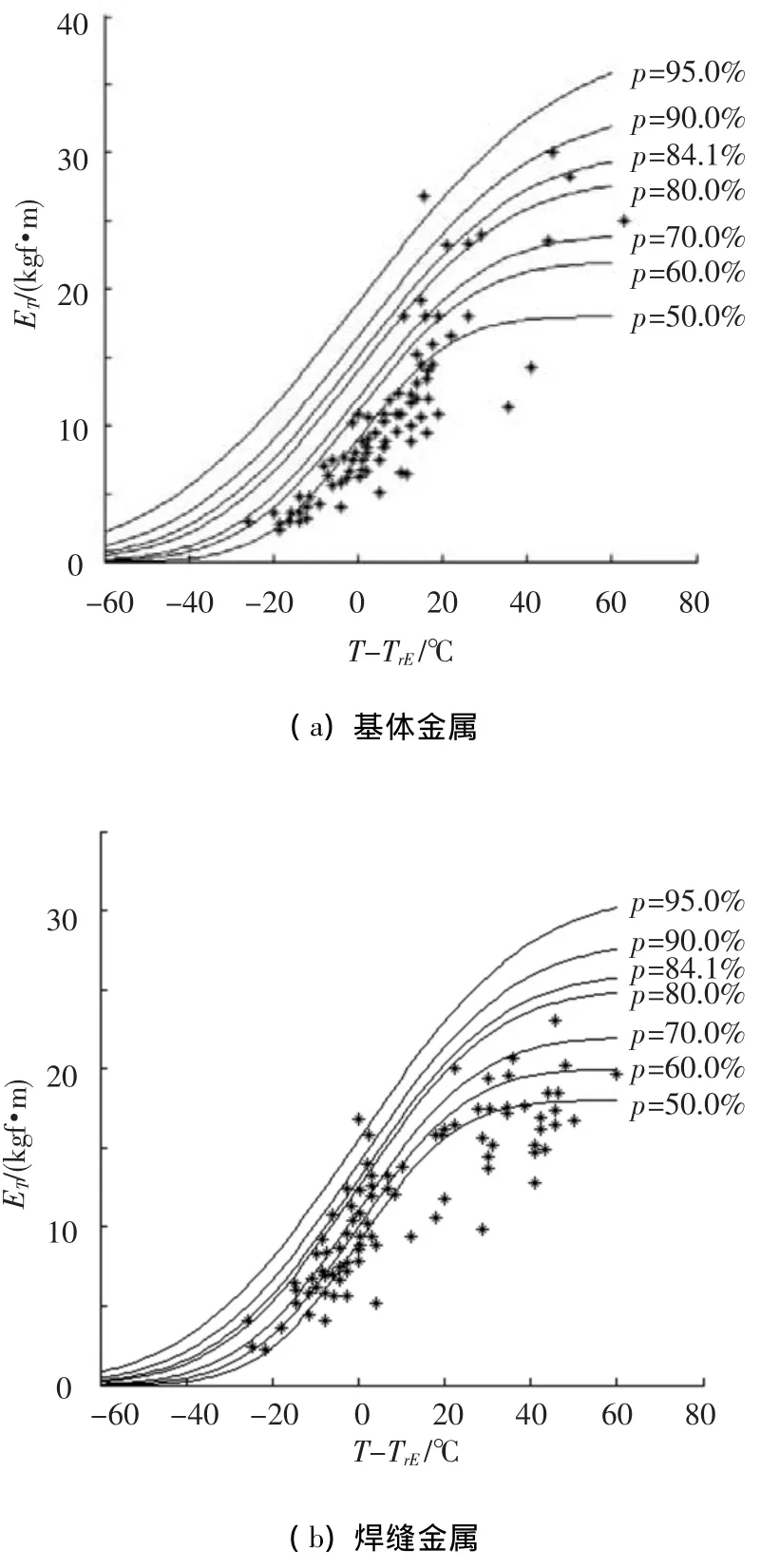
图8 不同可靠度下对应的拟合曲线

根据图8中不同可靠度的拟合曲线，采用“基于冲击试验吸收能确定材料断裂韧性”的方法，可以确定不同可靠度下任意等级钢板的韧脆转变温度.本文仅列出基体金属对应的韧脆转变温度结果，见表4.

表4 不同可靠度下焊接金属的韧脆转变温度

确定不同可靠度下材料的韧脆转变温度后，通过式(2)～式(5)，计算出不同可靠度下不同质量等级的低碳钢和高强度钢的断裂韧性值，本文仅列出可靠度为90%时基体金属中B级低碳钢的断裂韧性，结果见表5.

从表5中可以看出，B级低碳钢船用钢板的断裂韧性值与使用温度和钢板厚度呈近似的线性关系.基于最小二乘原理和多元一次拟合技术，可以建立断裂韧性KIC与使用温度T和钢板厚度t之间简单的函数关系:

对于其他可靠度下，基体金属和焊接金属中不同强度不同质量等级的船用钢板可获得相似的函数关系.根据这些函数关系，采用线性插值的方法可以确定任意可靠度下(50%～95%)不同钢板板厚和使用温度所对应的断裂韧性值.

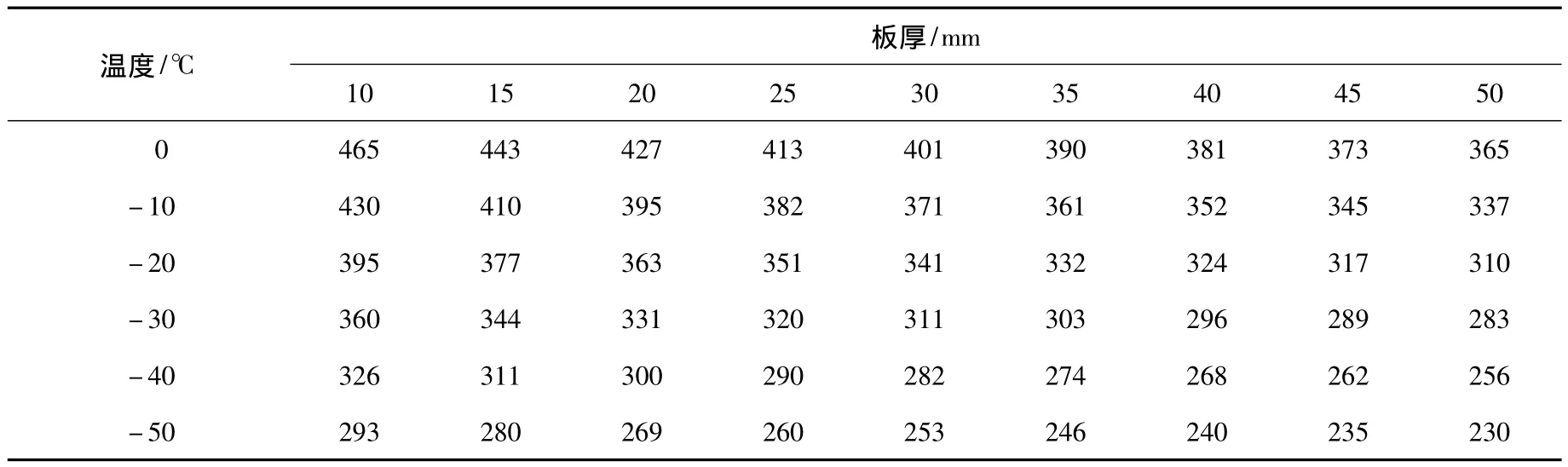
表5 可靠度为90%时基体金属中B级低碳钢的断裂韧性kgf·mm-3/2

4 结论

1)实现了根据夏比V型缺口冲击试验吸收能确定船用钢板断裂韧性的方法，建立了断裂韧性、试验温度和钢板厚度三者之间的函数关系，为低温使用条件下确定任意厚度船用钢板的断裂韧性提供依据.

2)提出不同可靠度下ET与T-TrE之间的函数关系，建立了可靠度为60%、70%、…、95%时与钢板厚度和试验温度分别呈线性关系的断裂韧性表达式，为获得任意可靠度下船用钢板基体金属和焊缝金属的断裂韧性值奠定基础.

［1］陈景杰.含裂纹损伤船体结构强度分析方法研究［D］.大连:大连理工大学，2011.

［2］GB4161—84金属材料平面应变断裂韧性KIC试验方法［S］.北京:中国标准出版社，1997.

［3］GB/T 229—1994金属夏比缺口冲击试验方法［S］.北京:中国标准出版社，1994.

［4］BARSOM J M，ROLFE S T.Correlations between KICand charpy V-Notch test results in the transition temperature range［C］//Impact Testing of Metals，STP 466，Philadelphia:ASTM，1970:281-302.

［5］ROLFE S T，NOVAK S R.Slow-bend KICtesting of medium strength high-toughness steels，recent developments in plane strain fracture toughness testing［C］//Review of Developments in Plane-Strain Fracture Toughness Testing，STP 463.Philadelphia:ASTM，1970:124-159.

［6］SAILORS R H，CORTEN H T.Relationship between material fracture toughness using fracture mechanics and transition temperature tests［C］//Proceedings of the 1971 National Symposium on Fracture Mechanics，Part II，STP 514.Philadelphia:ASTM，1972:164-191.

［7］ROBERTS R，NEWTON C.Interpretive report on smallscale test correlations with KICdata［J］.Welding Research Council Bulletin，1981，265:1-18.

［8］矢島浩.船体用鋼板の破壊靭性値推定手法に関する-考察［R］.長崎:三菱重工業(株)技術本部長崎研究所，1986:1-33

［9］矢島浩.船殼の脆性破壞管理制御に関する基礎的研究［D］.东京:东京大学，1980.

［10］WES3003低温钢板判定基准［S］.东京:日本焊接协会出版，1995.