大跨空间结构性能水准划分及其易损性分析

聂桂波，范 峰，支旭东

(哈尔滨工业大学土木工程学院，150090哈尔滨，nieguibo0323@163.com)

我国是世界上地震灾害最为严重的国家之一，地震区域广阔分散，地震频繁强烈.20世纪以来，震级8级或是8级以上地震就发生了近十次，给人民群众的生命安全及财产造成了惨重的损失.抗震设计的基本目的是保障生命安全，然而近十几年来大震震害却显示，按现行的以保障生命安全为基本目标的抗震设计理论所设计和建造的建筑物，在地震中虽然没有倒塌，基本保障了生命安全，但其造成的经济损失却异常巨大，这说明以生命安全为单一的设防目标是远远不够的.作为标志性建筑的大跨空间结构，其建设费用和震后修复费用相对较高，经济因素不可忽略，结构整个服役期的经济指标也成为设计时的一个关键因素，因此，以经济学、社会学和工程科学为理论基础的基于性能的抗震设计思想(performance-based seismic design，PBSD)具有良好的适用性，代表了结构未来的抗震理论发展趋势.基于性能的抗震设计，也称为基于功能(性能)的抗震设计，在90年代初期由美国科学家和工程师提出之后，很快被国内外众多学者接受，世界各国投入大量人力物力，积极展开这方面的研究工作.美国应用技术理事会(ATC)、联邦紧急事务管理局(FEMA)、加州结构工程师学会(SEAOC)等机构都围绕基于性能的抗震设计理论开展了一系列研究.ATC-40，FEMA-273和Vision 2000均制定了相应大纲，提出一系列性能目标，以及达到这些目标的设计和分析方法;《日本建筑法规》于2000年正式采用了基于性能设计概念的能力谱法［4］.随着理论研究的深入，考虑到结构抗震设计中存在着诸如外部荷载环境、结构本身特性和结构整体分析模型等不确定性，结构目标性能水平的优化决策应该充分考虑这些不确定性，国际结构安全度联合委员会(JCSS)于1997年发布了直接采用可靠度的全概率设计模式规范［5］.我国学者也一直在这方面的前沿领域开展工作，并取得了丰硕的成果［6-8］.基于性能抗震设计思想的提出，改变了以往抗震规范仅以生命安全为原则的单一设计方法，业主可以根据需要提出更高的结构预期抗震性能水准，设计灵活，并能在结构抗震性能和震后修复费用之间寻找到最佳的平衡点［9-10］，因此，这种抗震设计思想更加先进和完善.

近些年，基于性能的抗震设计理论研究在高层、高耸建筑等领域已经取得了很大进展.从这些研究可以看出，这一抗震思想的实施，是以对结构动力性能和强震破坏倒塌机理的深入理解作为基础.然而与上述结构相比，大跨空间结构由于其体系的特殊性，无论是从结构动力特性还是倒塌破坏规律方面都具有明显不同特点［11］，因此结构的分析手段以及在地震下的性能水准的描述也将明显不同，这些因素决定了在多、高层领域开展较多研究的基于性能的抗震设计方法，不一定完全适合于大跨空间结构，因此需对大跨空间结构展开针对性的研究，解决制约此类结构性能设计的关键理论问题.

本文通过考察国内外文献，结合空间结构自身特点确定了结构的性能水准，在此基础上，采用结构的损伤模型量化结构的性能水准，并采用多地震动的IDA分析方法，建立了各分级性能水准的易损性曲线，为建立完整的大跨空间结构基于性能的抗震设计理论奠定了基础.

1 结构性能水准的划分

结构的抗震性能水准是指结构在某一特定设防地震等级下预期破坏的最大程度，它涉及结构构件和非结构构件的破坏、建筑的使用用途及其内部物品的损失等因素，并且应综合考虑给定破坏状态下所引起的安全、经济和社会等方面的后果，因此划分结构的性能水准是基于性能的抗震设计理论首要解决的问题.ATC-40［1］，FEMA-273［2］和Vision 2000［3］分别给出了结构和非结构的性能水准，Ghobarah［12］参考上述组织的研究成果基础上，给出了高层结构的分级性能水准.我国的《建筑地震破坏等级划分标准》和《建筑工程抗震性能设计通则(试用)》(CECS160:2004)亦初步划分了结构的性能水准.我国许多学者在进行这方面研究时，都参考了上述文献及规范，例如刘艳辉等［13］参考《建筑地震破坏等级划分标准》给出了城市高架桥的五级性能水准;邓雪松等［14］对耗能减震钢结构进行了性能水准的划分;卜一等［15］划分了高层混合结构的分级性能水准;周云等［16］确定了高层钢结构的性能水准.

从上述研究成果不难看出，针对高层和高耸结构，众多学者进行了大量研究，由于高层和高耸结构分为明显的主要受力构件和次要受力构件，性能水准的选择也明显反应此类结构的力学指标，并且其在强震下的受力特点也与大跨空间结构有着明显不同，目前文献［17］对大跨空间结构中的代表结构形式——单层球面网壳开展了基于性能的初步研究，并对结构性能水准划分进行了探索，本文在此研究基础上，完善了单层球面网壳分级性能水准的划分，如表1所示.

表1 网壳结构性能水准的划分

2 结构性能水准的量化

国内外学者曾提出过许多参数来量化建筑结构的震害水平，包括强度指标、变形指标、能量指标、低周疲劳指标、变形指标、能量双重指标和结构损伤因子等.例如刘艳辉等［13］采用了混凝土压应变和钢筋拉应变量化城市高架桥的性能水准;Ghobarah［12］给出了以结构的顶点位移划分的性能水准.但这其中最常用的是采用变形(顶点位移或层间位移角)和结构的损伤因子这两种方式划分结构性能水准.例如卜一等［15］采用增量动力分析方法确定了高层混合结构的性能水准并以层间位移角限值作为量化指标;周云等［16］通过层间位移角量化高层钢结构的性能水准.由于结构失效时刻具有多项特征响应，分别表征结构不同的性能指标，这些特征响应之间既互相关联，又相对独立，因此结构的性能水准应该是多项响应指标综合的结果.而结构的损伤因子综合的考虑了结构的变形、能量、塑性发展程度等多项响应指标，因此更能够精确的刻画结构的损伤状态，所得到的分级性能水准也更加合理，采用损伤模型量化结构的性能水准代表了这一领域的发展方向，例如Park-Ang［18］建立了混凝土结构双参数损伤模型;在Park-Ang模型基础上，牛荻涛等［19-20］建立了混凝土结构改进的损伤模型并量化结构的性能水准;欧进萍等［21］在大量实际建筑结构的震害调查中，给出了应用损伤模型划分的性能水准.本文亦选择以结构的损伤模型量化结构的性能水准，具体做法是根据大量强度破坏算例计算结果的统计分析，提出结构的损伤模型，用此损伤模型刻画结构的损伤状态，从而达到量化结构的性能水准.

2.1 数值计算模型

以凯威特型单层球面网壳为研究对象(如图1(a)所示)，对结构施加了初始缺陷，统一取结构的第一阶振型模态，缺陷大小为L/300(L为结构跨度)，周边支承形式为三向固定铰支.网壳中每根杆件划分为3段，采用PIPE截面，沿每个截面有8个积分点，为说明杆件截面的塑性发展程度，定义1P表示至少有1个积分点进入塑性，8P则表示全截面进入塑性，余此类推.杆件截面满足常规设计要求，计算中采用Rayleigh阻尼，阻尼比取0.02，材料为Q235钢材.分析采用基于通用有限元软件ABAQUS编译的用户材料子程序［22］，可以模拟材料损伤累积和断裂的影响.子程序中材料损伤因子D定义为式(1)的形式，相应的钢材弹性模量和屈服强度如式(2)和式(3)所示，如此，则可将考虑材料损伤累积的本构模型应用于大跨空间结构的强震分析中.这个本构模型是通过文献［22］考虑空间荷载特性的影响，设计并进行多组圆钢管试件的空间滞回性能试验，考察了试件的空间滞回耗能能力;通过开发基于有限元软件ABAQUS的用户材料子程序，对试验进行了数值仿真模拟，拟合得到圆钢管考虑材料损伤累积的本构模型:

2.2 分析方法

目前被普遍接受的抗震分析方法是时程分析法，该方法对线性结构或非线性结构均适用，可以对结构直接输入地震动记录，能够完整地反映出结构在强震作用过程中结构响应的全过程，是工程中进行强震计算的主要方法.增量动力分析(incremental dynamic analysis，IDA)方法就是以非线性动力时程法为基础，分析结构在不同强震下的非线性响应.它能够考虑结构的抗震需求和地震的随机性，给出结构相应水准的可靠度，从概率角度描述结构的各项性能，因此是目前最有发展前景的结构抗震性能分析方法.这种方法通过对每条地震动记录不断调幅，形成一组不同强度的地震动，在这组地震动作用下对结构进行一系列的非线性分析，得出与地震强度因子相对应的结构性能参数，并在二维坐标里用曲线表达出来，即绘制IDA曲线，在IDA曲线上可以定义结构的倒塌极限荷载，可以了解结构的整个反应过程，即从弹性到屈服再到塑性最终进入整体动力不稳定状态.

IDA方法对结构的性能分析是通过结构的性能参数与相应强度因子的关系曲线来表现出来的，不同的IM与DM所能表达的结构的性能也不同，所得出的曲线离散性也不相同，因而需要选取合理IM与DM的表达方式.对于IM，一般要求可调、单调递增且与调幅系数成正比，满足要求的表达方式常有地面峰值加速度、地面峰值速度、谱加速度、结构屈服强度强度系数R等.对于大跨度空间结构IM的选用，目前尚未有文献提及，本文的IDA分析，采用PGA作为IM的参数.

2.3 结构损伤模型

对40 m和60 m的单层球面网壳通过50条地震动进行IDA分析，地震动选择原则是尽量避免采用近场地震动，同时也未选择远场地震动，而是选用了震中距在20～100 km的II类场地土类型下50条地震动.40 m单层球壳矢跨比为1/3，屋面荷载为60 kg/m2;60 m单层球壳矢跨比为1/3，屋面荷载为60 kg/m2.本文采用结构损伤因子DS来表示结构的损伤程度，该损伤因子以结构在地震下的多项响应为变量的函数，当DS=0时对应于无损状态，DS=1时网壳失效，在0～1内的其他数值表示结构不同的损伤程度.对各自变量进行无量纲化处理后，选择对各项自变量平方和开平方的形式来拟合单层球壳的损伤因子.通过对上述100条算例的整理，拟合得到结构的损伤模型为

式中:DS为结构损伤因子;L为球壳跨度;f为矢高;εa是结构平均塑性应变;εu为钢材极限应变;dm为最大节点位移;de是网壳材料出现塑性时刻的位移;r1是1P杆件比例;r8为8P杆件比例.用此公式重新计算结构破坏时对应的损伤值，如图1(b)所示，从中可以看到该损伤模型对应于倒塌时的损伤值大部分位于1.0左右，误差均在10%以内，证明该结构损伤因子具有良好的精度，可实现对结构损伤的精确刻画.

图1 单层球面网壳计算模型和损伤因子精度

2.4 结构损伤因子界限值与性能水准量化

在详尽考察结构在不同损伤因子下各项响应结果后，选取D=0.3、D=0.7和D=1.0作为结构轻微破坏、中等破坏、严重破坏和倒塌的界限值，之所以如此选取原因如下:在D=0.3时，结构在此时刚度未出现弱化，仅有数根杆件进入1P塑性，杆件基本完好，结构此时位移很小，因此将其作为轻微破坏和中等破坏的界限值;D在0.3到0.7之间，结构的刚度基本保持不变，但在这个区间内结构的塑性发展不断加深，杆件屈服较严重，位移均匀增加，因此将D=0.7作为中等破坏与严重破坏的界限值;而当D的值超过0.7时，随着损伤不断加剧，结构的刚度将出现明显的弱化，位移剧烈增加;而当D达到1时，结构倒塌.由此完成应用损伤因子量化结构的性能水准，如表2所示.

表2 网壳结构的分级性能水准与损伤因子限值

图2 结构各项响应统计

3 结构性能水准易损性分析

以往学者在进行结构的IDA抗震性能分析时，仅以结构的倒塌作为衡量结构损失的唯一指标，但实际情况却是，结构在未来遭遇的地震荷载作用下，虽然没有倒塌，但是结构却发生了不同程度的损伤，当损伤程度小时，不影响结构的使用，当损伤比较大时，却可能影响到结构的使用寿命，并且这种损伤必然造成了一定的结构损失，因此仅以结构的倒塌作为衡量结构发生损失的前提是不精确的.精细化的基于性能的抗震设计方法应该将不同程度的损伤引起的损失综合考虑，从而精确量化结构的损失.通过大量算例分析验证，本文提出的结构损伤模型与性能水准具有良好的对应关系，其具体描述见表1.对于选定的50条算例，对应于每一级性能水准，均可以将对应的地震荷载幅值得到，将这些离散点进行升序排列，并统计在给定的荷载幅值下的失效概率，即在任一给定地震动条件下，结构发生该性能水准的概率，也就是易损性曲线，如图3(a)～3(b)所示，即可得到结构在未来地震荷载作用下，任一状态的失效概率，从图中亦可发现，当地震荷载达到一定强度后，结构可能处于不同的损伤状态，不能仅以结构倒塌荷载作为评价结构性能的唯一指标，在进行结构基于性能的抗震设计时，可以此图作为参照蓝本，从而为基于“投资-效益”准则的结构性能评估和结构优化设计及结构风险评估奠定基础.

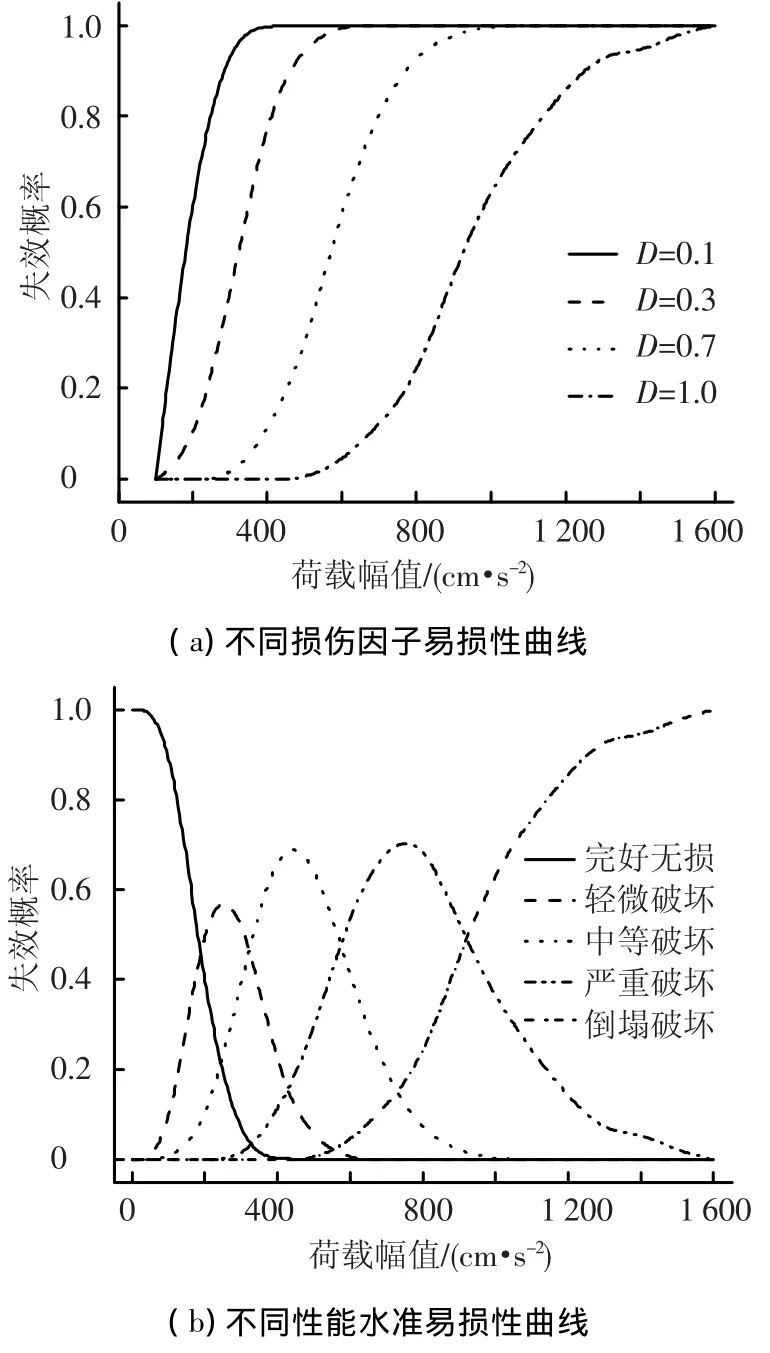
图3 结构分级性能水准和综合损失易损性曲线

4 结论

1)在详尽考察国内外文献基础上，确定了网壳结构的分级性能水准，并确定以结构的损伤模型作为性能水准的量化指标.

2)通过多组破坏时刻结构各项响应拟合，得到结构的损伤模型，考察了结构在不同损伤模型值下的响应规律，得到分级性能水准的界限值.

3)通过多组地震动IDA分析，得到结构分级性能水准的易损性曲线，为完善基于性能的抗震设计奠定基础.

［1］Applied Technology Council.Database on the performance of structures near strong-motion recordings:1994 Northridge，California，Earthquake［R］.Rep.No.ATC-38，Applied Technology Council，Redwood City，California:ATC，2000.

［2］Federal Emergency Management Agency.HAZUS-MH MR2 technical manual［R］.Washington，DC:Federal Emergency Management Agency，2006.

［3］Vision 2000 Committee.Performance-based engineering of building［R］.Oakland:Seismology Committee of the Structure Engineer Association of California，1995.

［4］小谷俊介.日本基于性能结构抗震设计方法的发展［J］.建筑结构，2000(3):3-9.

［5］KAZUHIKO K，TAKASHI K.Evaluation of indirect economic effect caused by the 1983 Nihowkai chubu earthquake Japan［J］.Earthquake Spectra，1990，6(4):739-756.

［6］汪梦甫，周锡元.高层建筑结构抗震弹塑性分析方法及抗震性能评估的研究.［J］.土木工程学报，2003，36(11):44-49.

［7］钱稼茹，罗文斌.建筑结构基于位移的抗震设计［J］.建筑结构，2001(4):3-6.

［8］王光远.抗灾结构的最优设防荷载与最优可靠度［J］.土木工程学报，1997，30(5):12-19.

［9］李刚，程耿东.基于投资-效益准则的结构目标性能水平［J］.大连理工大学学报，2005，45(2):166-171.

［10］STEWART M G.Acceptable risk criteria for infrastructure protections［J］.International Journal of Protective Structures，2010，1(1):23-40.

［11］沈世钊.中国空间结构理论研究20年进展［C］//第十届空间结构学术会议论文集.北京:中国土木工程学会桥梁及结构工程分会空间结构委员会，2002:38-52.

［12］GHOBARAH A.Performance-based design in earthquake engineering:state of development［J］.Engineering Structures，2001，23:878-884.

［13］刘艳辉，赵世春，强士中.城市高架桥抗震性能水准的量化［J］.西南交通大学学报，2010，45(1):54-58.

［14］邓雪松，汤统壁，周云，等.耗能减震钢结构性能水准与目标的初步研究［J］.防灾减灾工程学报，2008，28(1):104-108.

［15］卜一，吕西林，周颖，等.采用增量动力分析方法确定高层混合结构的性能水准［J］.结构工程师，2009，25(2):77-84.

［16］周云，王烨华，邓雪松，等.高层钢结构性能目标的建立［J］.钢结构施工，2007，22(5):1-6.

［17］支旭东，谢礼立.网壳结构损伤研究在性能抗震设计中的应用［C］//第十六届全国结构工程学术会议论文集.太原:中国土木工程学会桥梁及结构工程分会，2007:293-296.

［18］PARK Y J，ANG A H.Seismic damage model for reinforced concrete Journal of structural engineering［J］.ASCE，1985(4):722-739.

［19］邢燕，牛荻涛.基于结构性能的抗震设计与抗震评估方法综述［J］.西安建筑科技大学学报，2005，37，(1):24-34.

［20］陈新孝，牛荻涛.在役钢筋混凝土结构的地震破坏评估［J］.西安建筑科技大学学报，2002，34(4):305-308.

［21］欧进萍，何政，吴斌，等.钢筋混凝土结构基于地震损伤性能的设计［J］.地震工程与工程振动，1999，19(1):21-30.

［22］聂桂波.网壳结构构件空间滞回性能试验与精细化本构模型研究［D］.哈尔滨:哈尔滨工业大学，2008.