具有不同时间尺度的分布时滞竞争神经网络的指数稳定性
俞芳 由守科 杨红梅 秦丽华
(1.昌吉学院数学系新疆昌吉831100; 2.新疆大学数学系新疆乌鲁木齐830046; 3.昌吉学院初等教育学院新疆昌吉831100)
具有不同时间尺度的分布时滞竞争神经网络的指数稳定性
俞芳1由守科2杨红梅1秦丽华3
(1.昌吉学院数学系新疆昌吉831100; 2.新疆大学数学系新疆乌鲁木齐830046; 3.昌吉学院初等教育学院新疆昌吉831100)
运用分析方法结合微分不等式技巧研究了具有不同时间尺度的分布时滞竞争神经网络的指数稳定性,并取得了其指数稳定性的一个充分条件。
竞争神经网络;分布时滞;时间尺度;全局指数稳定性
引言
竞争神经网络是一种无监督学习型的神经网络,它模拟生物神经网络系统依赖神经元之间的兴奋、协调、抑制、竞争的方式进行信息处理[1-2]。具有不同时间尺度的竞争神经网络是一种特殊的竞争神经网络,这类神经网络有两类神经元:一类是短期记忆神经元(STM),一类是长期神经元(LTM),在不同类型的神经元中有不同的时间尺度[3-5]。从生物神经系统来看,人的大脑时刻处在周期和混沌状态,因此对神经网络的指数稳定性研究十分有意义。近年来,对于细胞神经网络、Hopfield神经网络、双向联想记忆神经网络的指数稳定性的研究已经取得了较丰富的结果[6-9],但对具有不同时间尺度的竞争神经网络的研究相对较少。文献[10]研究了带有时间变量和分布时滞的多时间刻度的竞争神经网络的指数稳定性,该文献主要侧重于研究该系统有唯一的平衡点。本文将研究具有不同时间尺度的分布时滞竞争神经网络的指数稳定性,推广了文献[10]的工作。
1 预备知识
考虑如下的具有时滞与分布时滞的竞争神经网络:

我们作如下假设:
(H1)函数αi(x)为连续与单调增的,即存在一个正对角矩阵A=diag(a1,a2,…,aN),使得对所有x≠y,i=1,2,…,N,有

(H2)函数fi(x)满足Lipschitz条件,即存在一个正对角矩阵K=diag(k1,k2,…,kN),使得对所有x,y∈R,i=1,2,…,N,有

系统(1)的初始条件为如下形式:

为了方便起见,下面介绍两种范数
对于任意的u(t)=(u1(t),u2(t),…,uN(t))T∈RN,定义范数如下:

对于任意的φ(s)=(φ1(s),φ2(s),…,φN(s))T∈RN,s∈(-∞,0]定义范数如下:

定义1.对于系统(1),如果存在正常数M及α,使得对∀t>0有下式成立
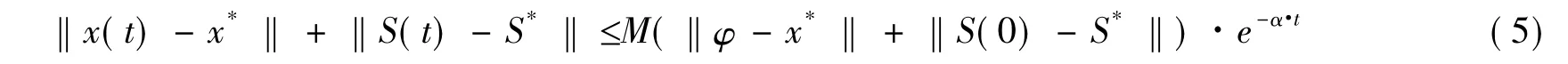
则系统(1)的平衡点(x1*,x2*,…,x*N,S1*,…,S*N)T为全局指数稳定的,其中α为收敛率.
引理1[11]令a,b≥0,s≥1,则有as-1
引理2[12]令a,b≥0,p≥q>0,则有
2 主要结果
定理1假设条件(H1)—(H3)成立,且满足下列条件:

则系统(1)为全局指数稳定的.
证明:从文献[10],我们易知系统(1)有唯一的平衡点(x*1,x*2,…,x*N,S*1,…,S*N)T,
令(x1(t),x2(t),…,xN(t),S1(t),…,SN(t))T为系统(1)的任意解,则有:

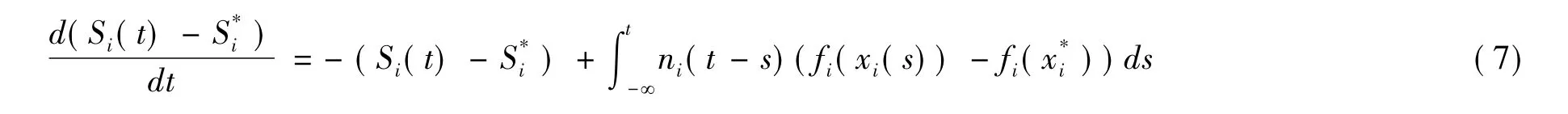
由定理1的条件,我们考虑如下函数:
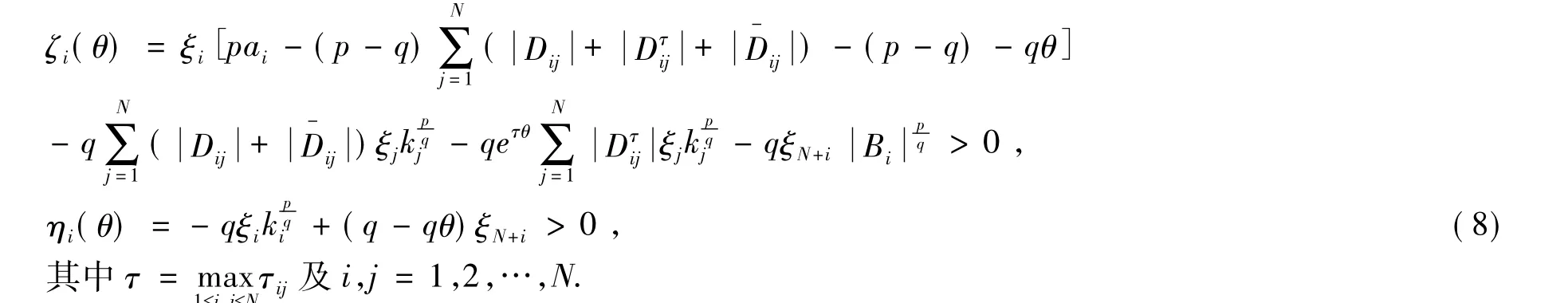
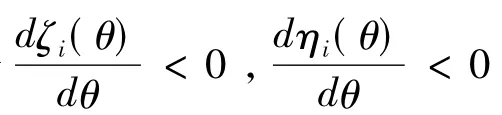

由式(9)及假设(H3),我们可选取一个非常小的正数,使得

利用(7)式、(11)式以及假设(H1)—(H3),我们取得同理可证:假设(16)式不成立,不失一般性,则存在某个i0和t*>0,使得







其中,由(18)式及引理2,可得到对所有t>0,有下式
成立.
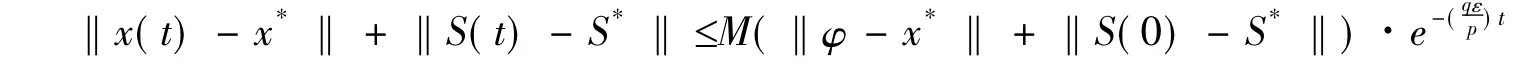
由定义1知,系统(1)全局指数稳定的.
推论1.假设条件(H1)—(H3)成立,且满足下列条件:

则系统(1)为全局指数稳定的.
证明:取定理1中的p=q=1,则(6)式变为(19)式,结论成立。
[1]王林山.时滞递归神经网络[M].北京:科学出版社,2008.
[2]杨建刚.人工神经网络实用教程[M].杭州:杭州大学出版社,1995.
[3]A.Meyer-Basese,S.S.Pilyugin,Y.Chen.Global exponential stability of competitive neural networks with different time scales[J].IEEE Trans.Neural Networks,2003,14:716-719.
[4]H.T.Lu,Z.He.Global exponential stability of delayed competitive neural networks with different time scales[J].Neural Networks,2005,18:243-250.
[5]H.Lu,A.Shun-ichi.Global exponential stability of multitime scale competitive
neural networks with nonsmooth functions[J].IEEE Trans:Neural Networks,2006,17(5):1152-11646.
[6]Qiu J.Exponential stability of impulsive neural networks with time-varying delays and reaction-diffusion terms.Neurocomputing 70(2007):1102-1108.
[7]J.G.Lu.Global exponential stability and periodicity of reaction-diffusion delayed recurrent neural networks with Dirichlet boundary conditions.Chaos,Solitions and Fractals,35(2008):116-125.
[8]桂江生,应义斌.混沌理论及其在建立神经网络模型中的应用[J].生物数学学报,2005,20(4):463-468.
[9]赵洪涌,王广兰.具有变时滞Hopfield神经网络的概周期解存在性与全局吸引性[J].数学物理学报,2004,24 (6):732-729.
[10][11][12]Yu Fang,Jiang Haijun,Teng Zhidong.Exponential stability of multitime scale competitive neural networks with time-varyng and distributed delays[J].新疆大学学报,2010,27(2):156-163.
(责任编辑:马海燕)
O175.13
A
1671-6469(2012)02-0081-05
2012-02-28
昌吉学院院级科研课题(2010YJYB008)
俞芳(1982-),女,山东烟台市人,昌吉学院数学系,助教,研究方向:常微分方程及其应用。

