一种基于改进Hausdorff距离的图像匹配方法*

甘新胜

(江苏自动化研究所,江苏 连云港 222006)

图像匹配技术是计算机视觉领域的一项关键技术在图像配准、模式识别、目标跟踪等方面都有应用。图像匹配通常提取两幅图像的特征点形成特征点集,再通过相似性准则描述两个点集的相似度。特征点可以是边缘点、角点等。通常特征点选取在噪声、光照、成像角度等变化下均能检测到的特征,具有较强的稳定性。图像匹配考虑的是两幅图像特征点集的相似性,如果不考虑特征点的提取过程,影响两个图像点集匹配的主要原因是遮挡、局部变化等因素。选择正确的相似性准则是图像匹配过程中一个重要的步骤。

Hausdorff距离(HD)的原始定义噪声敏感,很难在实际的图像匹配中应用。通过对HD的改进能够消除其本身存在的局限性,Huttenlocher等人[1]提出了部分HD,将最小距离排序再取其中的一个,该改进消除了噪声的干扰,但在实际应用中,部分比例设置的精确程度影响匹配的效果。Dubuisson等人[2]提出了均值HD(MHD),计算过程中把噪声也用于计算,在实际应用效果不如部分HD。Azencott等人[3]提出了一种Censord HD(CHD),该改进需要两次排序,计算复杂度较高。Sim 等人[4]基于M-估计和最小截取二乘法提出了M-HD和LTS-HD,两者均是屏除噪声点进行计算,与 PHD一样存在参数的设置问题。汪亚明[5]在 LTS-HD和 M-HD基础上提出了鲁棒性HD(RHD),RHD依赖于两个参数的设置,而且在计算过程进行伪边缘去除,这个操作复杂度较高,在实际匹配中无法准确判定哪些是伪边缘。改进的一种形式是加权 HD(WHD)[6～9],这种方法通常用于面部识别、文字识别等能够预先知道物体的各个部分的空间分布。HD不要求匹配双方建立一对一的点对应的,而是关注两个匹配点集的最大不匹配程度。本文在分析传统HD方式的缺陷,并提出了基于核函数的HD测度,该HD是通过对各个最小距离值进行核函数计算,并将函数值的和均值作为单向 HD 值,无向的HD值取两个单向值的最小值。

1 Hausdorff距离及其改进形式

给定两个有限点集 A={a1,a2,…,ap}和 B={b1,b2,…,bq},它们之间的Hausdorff距离定义如下:

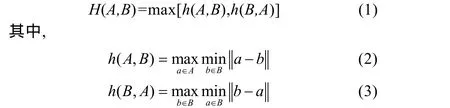
在上两式中,范数||⋅||可取不同形式,如 L1,L∞和 L2等。h(A,B)称为集合A与集合B的有向Haudorff距离(前向HD),描述了点a∈A到点集B中任意点的最大距离;同样,函数h(B,A) 称为从集合B与集合A的有向Haudorff距离(逆向HD),描述了点b∈B到点集A中任意点的最大距离。由于h(A,B) h(B,A)不对称,所以一般取它们两者之间的最大值作为两个点集的Haudorff距离。如果两个点集的HD为0,就说明这两个点集是重合的。从定义可以看出,如果两个点集的大部分点都一样,但只有很少甚至一个点不一致,得到Hausdorff距离就会较大。说明Hausdorff距离对外点很敏感,针对这个问题,人们提出了很多的改进方法[1-9]。

影响两个点集的匹配的主要原因是遮挡和两点集间的局部变化。如果预先能够知道模板物体在图像中的被遮挡的比例,那么通过设定 PHD的比例即可能够实现正确的匹配,但在实际情况中很难知道精确的比例,有时知道大致的比例也不能得到正确的结果。如图1所示,当比例f为0.395时能够得到正确的匹配,但取 0.39和 0.4均不能得到正确的结果。同样的实验,MHD不能得到正确的匹配,而且M-HD、LTS-HD在参数设置稍大时不能得到正确的匹配。局部变化影响 HD匹配的结果是在第一阶段的最小距离集合中存在大量分布在0点附近的值。典型的例子如不同季节的航拍图像匹配,道路或者其它物体被植被的遮挡情况不同,从而出现原来直线的道路被扭曲了。

遮挡、局部变化使得最小距离的分布集中在 0值附近,从而出现在某个阈值下,该部分占据的比例达到最大。为了克服遮挡、局部变化对匹配的影响,计算单向 HD值时引用核密度函数的方式,集合A➔B的单向HD值计算如下:

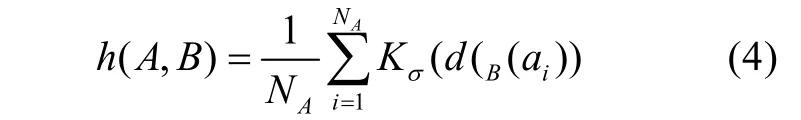
式中,ai为集合A的成员,NA是模板A的点数目,dB(ai)表示点 ai到集合 B的最小距离,Kσ是核函数,σ为带宽。B➔A的单向HD值为

其中,N’B为在模板 A覆盖下的点数目,要求 N’B＞0。通过对最小距离值的分布分析知道,在匹配位置的分布通常接近于高斯分布, Kσ可以取高斯函数:

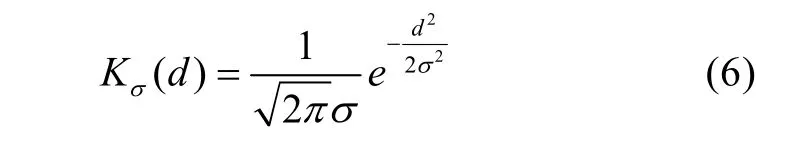
其中,σ2表示方差,d为最小距离。H(A,B)通过式(7)得到:

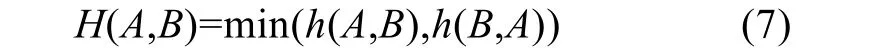
当两幅图像越相似,H(A,B)越大;反之越小,而匹配点就是函数值的极大值点。通过参数σ2的设置从而决定最小距离在零附近的值起到的作用,当局部变化较大时,σ2取大一些,相反就小一些,通常来说σ2取1～5。从式子可以看出,当核函数取不同的函数得到不同的结果,如取恒指值就是MHD,而M-HD是一种分段函数。使用高斯能够较好的考虑最小距离集合中的低频部分,低频部分的距离值越大,最终取值越大,消除简单的单一阈值的划分导致的匹配错误。

图1 合成图像

2 基于HD的图像匹配过程

图像匹配通常是模板和图像的匹配,即一副图像为模板,一副为图像,模板在图像中搜索物体存在的位置。基于HD的图像匹配过程如图2所示,主要包括三步:首先是特征提取,角点、边缘点提取。角点提取可以采用Harris、SUSAN等算法。其次对提取的特征图像进行距离变换,目的是为了减少HD的计算量,距离变换根据实际要求选取,两次扫描就能得到距离图[10]。然后利用距离图进行搜索,移动模板在图像上搜索,计算每一锚点上的 HD 值,选取极值为最佳匹配点。通常来说首先计算前向 HD,只有前向HD值小于或大于某个值才进行逆向 HD的计算,这样可以减少不必要的计算。如果模板与图像的存在形变,还需要对模板进行几何变换,再重复前一过程的搜索。通常来,计算逆向HD时,不取全图像的数据进行考虑,而只考虑被模板覆盖的部分[1]。

图2 基于HD距离的图像匹配过程

3 实验结果与分析

为了测试改进 HD的性能,将对 PHD、MHD、M-HD、LTS-HD、本文方法等进行实验分析。首先设置处理的参数。距离变换算法为串行计算,相邻距离为 3,对角距离为 4,具体实现见文献[10]。其次是改进HD的算法设置。实现与原算法不一致的地方在于M-HD和LTS-HD在文献[5]中并没有给出逆向(B➔A)的计算方法,这里增加了逆向计算,参数与正向(A➔B)一致;各个改进HD的参数设置见表1。

实验分为两组,第一组实验使用图1的图像进行匹配,图像来源于文献[4],模板的实际位置为(37,29)。实验二是一副经典图像并经过了涂抹,模板的实际位置为(37,60),效果如图3,准确匹配的合成效果如图4所示,与图1(c)的合成思路一样,在图像上叠加模板边缘图像。叠加显示可以直观的反映出匹配的结果。匹配正确,对应位置的边缘将保持图像的边缘,在图像上没有而模板有的边缘将添加;如果匹配位置不正确,边缘一致在合成图上将出现重影,边缘加重,如图5是在(35,60)位置进行合成得到的效果图,从中可以看出,在模板框内本应重叠的帽沿部分出现边缘加重,原因是叠加图本应是一条边缘,但现在出现了两条。

实验结果见表1,从中可以看出,①均值HD在两次实验中都没有得到正确的匹配;②部分HD依赖于比例参数f的设置,有时要求设置非常精确才能够得到正确的匹配;③M-HD 取得正确结果也依赖于τ的设置,第一组实验为5,第二组实验为6,当取值较大时不能得到正确匹配,原因是,τ越大,用于计算HD值的点越多,噪声点越多,偏差也就越大,同样事情也发生在LTS-HD;④本文算法在两组实验中都能得到较好的匹配结果,都能找到正确的匹配位置。

图3 匹配图像

图4 边缘及匹配结果

图5 错误匹配的合成效果,合成为位置为(35,60)

表1 各个算法的实验结果

4 结束语

Hausdorff距离的应用十分广泛,不同的应用领域都有自身的特点,也就有不同的改进方法。通过实验分析得到,基于核函数的 Hausdorff距离在图像匹配具有较强的鲁棒性。HD距离经过了研究,但还有很多问题,如计算量大问题。未来的研究将结合变换参数进行匹配研究,并考虑在搜索策略进行改进。

[1]Huttenlocher D P, Klanderman G A, Rucklidge W J.Comparing images using the Haudorff distance[J].IEEE Transactions on Pattern Analysis and machine Intelligence,1993,15(9):850-863.

[2]Dubuisson G P, Jain A K. A modified Haudorff distance for object matching[C]. Proceedings of the 12thIAPR International Conference on Pattern Recognition, Jersusalem,Isr:IEEE press,1994:566-568.

[3]Azencott R, Durbin F, Paumard J. Multiscale indentification of building in compressed aerial scenes[C]. Proceedings of 13thInternional Conferences on Pattern Recognition, Vienna,Austria:[s,n.].1996:974-978.

[4]Sim D G, Kwon O K, Park R H. Object matching algorithm using robust Haudorff distance measures[J].IEEE Transactions on Image Processing, 1999,8(3):425- 429.

[5]汪亚明.图像匹配的鲁棒性Hausdorff方法[J].计算机辅助设计与图形学学报,2002,14(2):1-4.

[6]Lu Y, Tan C. Chinese word searching in imaged documents[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2004,18(2):229-246.

[7]Lin K H, Lam K M, Siu W C. Spatially eigenweighted haudorff distances for human face recognition[J]. Pattern Recognition,2003,36(8):1827-1834.

[8]Guo B F, Lam K M,Siu W C, Yang S. Human face recognition using a spatially weighted Hausdorff distance[C].IEEE International Symposium on Circuits and Systems, Sydney, NSW:Institue of Electrical and Electronics Engineers Inc,2001:145-148.

[9]Lu Y, Tan C L, Huang W, Fan L Y. An approach to word image matching based on weighted hausdorff distance.[C],Seattle,USA ‘ 6thICDAR’,10-12,Sept,2001,

[10]章晋毓.图像工程(中册)[M].北京:清华大学出版社,2007:63.