作战系统的序参量及其演化方程
李 丹,于小红
(装备指挥技术学院,北京 101416)
“新三论”是继信息论、系统论、控制论(“老三论”)之后发展起来的新兴横断学科,主要包括耗散结构论、协同学和突变论。“新三论”与“老三论”相比,在揭示对象本质上更为深刻,应用也更为广泛,在现代科学领域起着不容忽视的作用。本文将“新三论”引入到作战系统研究中,从系统科学的角度出发,研究作战系统这个复杂的非线性系统,指出作战系统的序参量,建立序参量方程,分析序参量演化稳定性与途径,旨在探索作战系统发展演变规律,为作战系统建设提供理论依据和方法论支持。
1 作战系统发展演化的序参量
根据协同学理论,在系统的演化过程中,并不是所有的参量对系统演化起一样的作用,只有序参量才起决定性作用。序参量决定系统是否变化,以及变化的方向,是发展为一种新的更有序的态,还是退化为无序的态,甚至分岔、混沌、直到衰亡。序参量具有如下特征:序参量是一个宏观参量,它是系统内部各子系统集体运动的产物,是合作效应的表征和度量,同时序参量支配着子系统的行为,主宰着整个系统的演化过程[1-2]。影响作战系统发展演化的变量有很多,作战能力是其中从始至终都起作用,主宰整个系统发展演化过程的序参量。
首先,作战能力是一个宏观参量。《中国人民解放军军语》(1997年版)中作战能力的定义是:武装力量遂行作战任务的能力。由人员和武器装备的数质量,编制体制的科学化程度,组织指挥和管理的水平,各种保障勤务的能力等因素综合决定。也与地形、气象及其他客观条件有关。可见,作战能力并不为作战系统中某个子系统所独有,不是一个单个要素,并不是各作战单元作战能力的简单叠加,而是各子系统能力和作用合成所表现出的综合效能。
其次,作战能力不是由系统外部指令或驱动而产生的,而是系统内部各子系统相互作用、相互协同的而“涌现”出的整体功能,它是作战系统内部各子系统集体运动的产物,作战能力表示作战系统的有序结构和类型,它是子系统介入协同运动程度的集中表现。作战能力的大小能够用来衡量一个作战系统的好坏,它是作战系统中各个子系统合作效应的表征和度量。
最后,作战能力支配着各个子系统的行为,主宰着整个系统的演化过程。作战能力是使作战系统丧失旧的稳定性而向新的更高的稳定有序结构跃变的“不稳定模”,是极其活跃、能够支配作战系统演化并主宰演化进程和结局的重要参量。作战能力发展的程度决定了系统的性质和水平,它对作战系统的要素都起着支配和决定的作用。作战系统发展演化都是以提升其作战能力为根本出发点的,比如,编制体制调整、武器装备改进与研发和人员培训等都是围绕提升作战能力而展开的。作战能力起到促使作战系统中各个子系统向有序化和有结构的方向发展,子系统间互相协同,使系统丧失旧有的稳定性,进入不稳定区域,最后达到新的稳定。
2 系统发展演化的序参量方程
序参量在作战系统演化和发展过程中起着主导和支配作用,及时准确地发现并把握作战系统序参量的变化,是把握作战系统发展演化的关键。为此,通过建立作战系统序参量演化方程来分析作战系统发展演化过程。协同学认为,系统内部的竞争和合作方式受控制参量的影响,控制参量的变化驱使系统经历一系列临界点,导致序参量的出现、竞争和合作,从而形成各类不稳定模和有序结构。由于作战系统是一个有势系统,因此可以运用突变论来建立序参量方程。
信息化条件下作战是以信息网络为支撑,将各种不同功能的武器子系统,如目标探测、跟踪识别、指挥控制、态势感知等合成一个整体系统。同时,将整个作战空间的武器平台、指挥控制、态势感知等合成一个精干而密切协同的有机整体,表现在力量编成上就是通过信息的“耦合”作用,实现“单元个性优势与系统效能的完美结合”,呈现出信息主导下的不同作战单元功能耦合的整体性。可见,作战系统的整体作战能力取决于武器装备自身的作战能力和作战网络的结构力两个因素。结构力强则作战系统内部各要素运行协调,能够产生最大的结构能。可见,作战能力的产生是作战力量的作战能力(本文称之为作战系统的基础作战能力)和作战力量间的协调程度(本文称之为作战系统的协同力)共同作用的结果。为此,本文确定作战系统的控制变量为作战系统的协同力u和基础作战能力v为控制参量,而将作战系统的序参量作战能力定义为状态变量x。另外,确定作战系统的协同力u和基础作战能力v为控制参量的合理性也可以通过文献[3]-[5]的相关内容得到印证。
根据突变论可知,基本的突变数目取决于控制变量的数目,当控制变量不大于4个时,最多有7种突变形式[6]。由于作战系统的控制参量为2个,状态参量为1个,因此,可以选择尖点突变模型,其势函数为

则作战系统序参量方程为

式(2)表明,作战系统是非线性系统。在作战系统的演化过程中,非线性发挥突出的作用,这种非线性作用是系统形成有序结构和产生复杂性的内在动因。在非线性的相互作用下,作战系统内部各要素之间通过相互作用而相互关联并形成协同,这种协同使作战系统产生整体行为,使得系统局部的小涨落得到放大,从而引起系统从稳定到非稳定再到新的稳定的跃迁式演化。
3 序参量演化稳定性与途径
根据自组织原理,稳定性是系统的重要维生机制,稳定性越强,意味着系统的维生能力越强。从实际应用角度看,只有满足稳定性要求的系统,才能正常运转并发挥功能。及时准确地发现和把握作战系统序参量的变化,是控制系统稳定有序的关键。作为一种动力学特性,系统理论关心的首先是演化方程解的稳定性。因此,本文通过分析作战系统序参量演化方程的解的稳定性,进而分析其序参量演化不同途径的形成原因。
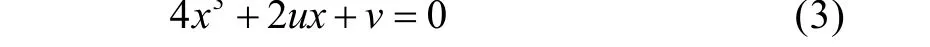
式(3)是由系统所有的临界点集合而成的平衡曲面M。由于式(3)是一个三次式,它或者有一个实根,或者有三个实根,实根的数目由判别式Δ=8u3+27v2决定[7]。如果Δ≤0,则有三个实根,否则只有一个实根。除非Δ=0,根各不相同,而Δ=0时,如果u和v均为非零,则所有两个根相同,如果u和v均为零,则所有的根都相同。这说明Δ<0时,V有两个极小值,一个极大值,即两个稳定的平衡点。Δ>0时,V只有一个平衡点。而Δ=0时,就是状态发生变化的地方。也就是说,如果控制变量满足Δ>0时,作战系统处于稳定状态;如果控制变量满足Δ≤0,则作战系统会发生突变现象,即作战系统由稳定趋向振荡、错位、混乱直至陷于崩溃。
令V''(x)=0,得该平衡曲面的奇点集:
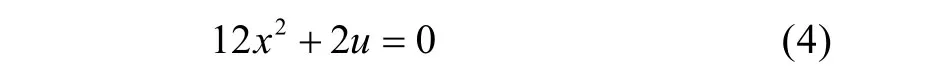
由式(3)和式(4),消去x,可得突变模型的分歧集方程:

序参量方程演化的尖点突变的平衡曲面和分歧点集如图1所示。图1中曲面ABCD是一个折叠的曲面,OL为基础能力水平轴,OX为协同能力水平轴。假若系统的状态是以x,u,v为坐标的三维空间的一个点来代表的,则相点必定总是位于曲面上,事实上,它必定总是位于曲面的顶叶或低叶。因为中叶对应于不稳定平衡。如果相点恰好在曲面终止的边缘上,则它必定跳跃到另一叶上,这引起x的突变。

图1 尖点突变的平衡曲面和分歧点集
从突变模型上来看,如果基础作战能力和协同力都达不到阈值,截距对应于OL轴和OX轴的M点和N点,与底平面上小四边形MONV相对应的曲面,就是不发生折叠的部分。同样地,协同能力再强,如果基础能力在阈值以下也不能具有良好的作战能力。只有当二者都超过阈值点时,作战系统才可能有良好的作战能力,即有作战能力突变的可能。UVW 三角区表明作战系统的基础作战能力和协同能力及作战能力的最佳比例。
下面将突变理论引入到作战系统稳定性分析中,用突变理论研究其不连续现象。
1)作战系统中存在着涨落和随机变量,当系统涨落时各种元素相互竞争,通常的作用结果是此消彼长,千变万化,杂乱无章,瞬息即逝。但是其中的某些因素有意或无意地协同作用时,如果具备基本的条件,系统的涨落就会趋于某个方向,作用结果就会不断放大,达到一定阈值,就可能出现跃迁,产生新的有序的系统。阈值联系于临界状态的相变点,它是一个可能产生不同结果的分岔点。涨落对达到阈值有一个放大作用。这是必然性(基本条件、一定阈值)和偶然性(涨落、分岔点)的统一。
可见,序参量的形成动因来自于系统内部,当众多子系统构成的系统处于无序初始状态时,各子系统独立运动,各行其是,不存在合作关系,不能成为序参量。只有当系统接近临近点时,子系统间产生关联,形成协同关系,这时序参量形成,它标志着系统进入一个新的有序态。作战系统序参量稳定态依赖于系统内部控制量,系统内的控制参量对系统序参量的演化起着决定作用。
因此,必须充分发挥序参量在系统转化和发展过程中的主导和支配作用,从而把握系统发展的方向。要发挥“序参量”在作战系统主导要素的积极作用,而且不断向该系统内注入新鲜活力,使整个作战系统始终保持鲜活、旺盛的发展势头,并形成良性循环。在具体作战行动中,要求作战指挥员必须做到:一方面,当作战系统处于无序状态时,要周密分析,准确把握并捕捉“序参量”,使其在关键时刻发挥关键作用,以扭转局面,实现无序状态向有序状态的转变。另一方面,当作战协同系统处于有序状态时,指挥员要保持清醒的头脑,对当前的战场情况要有高度的警觉性,时刻观察和发现战场情况的变化,不要被表面现象所迷惑。
2)作战系统发展存在两种演化方式即渐变和突变。在系统自组织演化过程中,突变和渐变是互相联系的。根据突变论,相变过程既有可能是突变也有可能是渐变。事物的渐变或突变与事物本身所处的状态密切相关。在严格控制条件下,如果质变经历的中间过渡态不稳定,那么它就是一种突变过程;如果中间过渡态稳定,那么它就是一种渐变过程。从图1可知,在大多数情况下,作战能力是渐变的过程,而在特定情况下,作战能力会发生突变。作战能力发生突变严重受到协同力的影响,作战系统的“协同力”一方面有助于维持作战系统与外部环境进行有序地物质、能量和信息交换,并促使作战系统内部各要素之间形成功能上的互耦、空间上的互倚和效能上的互补关系,从而使得作战系统呈现出明显的整体性,产生出远远超出各组成要素单独作战能力之和的作战能力,也就是作战能力呈现出“涌现性”。但另一方面,协同力太强的话,也会带来一些副作用,它可能给作战系统带来整体结构转型或坍塌的风险。在作战双方对抗的过程中,当作战力量结构出现损伤,信息链式运动遭受破坏等等,作战系统的构成要素就可能发生突变。为此,我们把突变区分为不利的灾难性突变(即灾变)和积极的建设性的突变(即建变)两种。可见,将突变理论引入到作战系统研究中,对于指导我们引导建变,防止灾变,做出最优化的决策,无疑具有很大的意义。
4 结束语
近年来,运用系统科学理论研究作战问题在国内外得到了普遍重视。为了探讨作战要素之间的协同问题,从作战系统的自组织特性出发,本文运用“新三论”研究作战系统的序参量及其演化方程。通过引入作战系统序参量的概念,建立序参量方程,可以用来分析作战系统发展演化过程,探索作战系统发展演化规律。运用该方法可以定量地分析作战系统在什么情况下会发生突变,从而引导渐变,防止突变,这对于指导作战系统建设和优化无疑具有重要意义。但是,作战系统相对于其他作战系统还存在对抗性、相对性等特点,应深入开展对抗条件下作战演化机理的研究。
[1][德]H.哈肯.信息与自组织复杂系统的宏观方法[M].成都:四川教育出版社,1988:65.
[2]曾健,张一方.社会协同学[M].北京:科学出版社,2000:30-33.
[3]王三喜,等.联合作战力量协同机理研究[J].复杂系统与复杂性科学,2011,8(1):11-12.
[4]王振宇,马亚平等.基于“联合指数”的作战效能评估方法研究[J].计算机仿真,2006,23(3):8-11.
[5]苗海军,刘正威,等.基于“联合指数”的联合作战编组集团能力量化分析[J].海军工程大学学报,2006,18(5):105-106.
[6]孙中一.耗散结构·协同论·突变论[M].北京:中国经济出版社,1989:104.
[7]何平,赵子都.突变理论及其应用[M].大连:大连理工大学出版社,1989:16.

