反舰导弹仿真中的目标命中判断
邱 杰
(海军航空工程学院,山东 烟台 264001)
对于反舰导弹而言,通常要求能够直接命中目标舰艇(以下将直接命中简称为命中)。在反舰导弹/水面舰艇攻防对抗研究中,反舰导弹能否命中目标舰艇,命中目标舰艇的什么部位,命中目标舰艇后侵彻到什么深度后爆炸,以及爆炸后产生的破坏效果如何,等等,都是非常重要的问题。这些问题,在很大程度上需要通过系统仿真来进行研究和解决。
系统仿真(本文中的仿真专指数字计算机仿真)的价值和生命力在于真实。要仿真真实必须模型真实。但是,仅此是不够的。因为模型本身并不能直接在计算机上运行,在计算机上运行的只能是仿真程序。因此,仿真程序还必须精确地反映模型,这要通过模型校核来保证。
导致仿真程序不能精确地反映模型的因素和问题很多,本文主要针对反舰导弹仿真中的目标命中判断,研究其中的系统状态不连贯的问题,并提出一种新的解决方法—预测法。该方法已经得到成功的应用。
1 模型校核的意义和作用
从20世纪60年代开始,针对系统仿真的固有特点,人们开始将保证仿真真实的相关问题条理化和阶段化,提出了VV&A的概念。
VV&A 中的 A(Accreditation)的含义是认定,表示权威机构的认可。
VV&A中的第一个 V即 Verification。对于Verification有多种中文译法,比较有代表性的有两种,一种译为校核[1-3],一种译为确认[4]。从保证模型到实现(计算机实现,即仿真程序)的精确度的角度看,译为校核较为确切。
VV&A中的第二个 V即 Validation。对于Validation也有多种中文译法,比较有代表性的有两种,一种译为验证[1-3],一种译为确认[4],从保证模型有效性(即模型真实)的角度看,译为验证较为确切。
本文中研究的系统状态不连贯的问题属于模型校核的范畴。
系统仿真的三个基本要素是[5]系统、模型(通常指数学模型)、计算机。联系这三个基本要素的三个基本活动是数学模型建立、仿真模型建立/仿真程序建立、仿真试验。这些基本要素及基本活动之间关系如图1所示。
由图1可见,仿真模型的建立反映了数学模型和数字计算机之间的关系。从严格的意义上讲,实际系统在时间上都是连续的,而计算机(指数字计算机,下同)是无法对连续时间进行直接处理的。因此,必须对数学模型进行离散化以使其能够为计算机所接受。数学模型离散化的结果是产生仿真模型。
显然,仿真模型还不能直接在计算机上运行,还必须利用计算机程序设计语言将其转换成为计算机程序,即仿真程序。由此可见,在仿真中,要从数学模型得到仿真程序,必然要经过两次转换,即从数学模型到仿真模型的转换和从仿真模型到仿真程序的转换。在任何一次转换中都有可能出现错误,这样的错误在本文中称为模型校核问题。
模型校核是验证仿真程序是否精确地实现了数学模型,即验证仿真程序运行时产生的行为与数学模型所描述的系统行为是否一致。如果不一致,则可能是在由数学模型导出仿真模型时有错,或者是在由仿真模型导出仿真程序时有错,或者在这两个过程中都有错,因此必须检查、修改仿真模型和/或仿真程序。
2 系统状态不连贯的问题
2.1 系统状态不连贯的基本概念和例子
本文中,“不连贯”一词是对英文 discontinuity的翻译。一个表征系统(或其中的一个部分或者一个方面,以下不加区分)行为或特征的状态(即系统状态)可能具有多种差别较大的不同取值,系统状态不连贯指的是其从一种取值突变到另一种取值。系统状态不连贯往往与系统演进过程中的重要事件同时发生。
在现实世界中,系统状态不连贯随处可见。这里举两个例子。
1)第一个例子:乒乓球的下落
一个人站在地板上,让手中的一个乒乓球自由下落。乒乓球在触碰地板前,其运动状态是由高到低,一旦触碰到地板即会反弹,其运动状态变为由低到高。在这个例子中,乒乓球的运动状态是突变的,突变的原因是发生了乒乓球触碰地板,这个突变是与乒乓球触碰地板这一重要事件同时发生的。
2)第二个例子:反舰导弹攻击目标舰艇
在反舰导弹临近目标舰艇时,由于俯冲,会由空中进入水中,再由水中进入目标舰体(即命中目标)。反舰导弹的运动状态由空中飞行到水中运动是突变的,突变的原因是发生了反舰导弹入水。同样地,反舰导弹的运动状态由水中运动到在目标舰体中运动也是突变的,突变的原因是发生了反舰导弹命中目标舰艇。
2.2 系统状态不连贯的问题
现实世界中的系统状态不连贯本身没有问题,也不会让人产生困惑。在仿真中,对于系统状态不连贯建立数学模型通常也不会产生问题。
对于上述的乒乓球的例子,略去乒乓球反弹到达最高点后的部分,可以建立如下的数学模型。
模型的描述:
以地板的高度为0,忽略空气阻力,重力加速度设为a,乒乓球在距地板高度为H0的位置,在 0时刻从静止状态自由下落,触碰(弹性碰撞)地板后,以触碰地板时的速度为初始速度向上运动。求乒乓球的高度随时间的变化。
模型的数学表达式:
以H(t)表示t时刻乒乓球距地板的高度,以t1记乒乓球触碰地板的时刻,有:

式中,t1=是乒乓球触碰地板的时刻。
上述关于乒乓球运动的数学模型无疑是正确的。但直接基于上述数学模型导出的仿真模型以及针对仿真模型编制的仿真程序通常会出现问题。
仿真程序是按离散的仿真时间点一步一步推进的。从理论上看,乒乓球触碰地板的时刻与某个仿真时间点重合的概率等于零。考查乒乓球下落过程中的一个仿真时间点,此时乒乓球尚未触碰地板,之后乒乓球应该继续向下运动。如果乒乓球距离地板尚远,继续向下运动没有问题;但如果乒乓球距离地板已经很近,继续向下运动的乒乓球会在下一个仿真时间点之前触碰地板。发生后一种情况(或迟或早必定会发生)时,仿真中的乒乓球就会钻入地板,然后在下一个仿真时间点再沿着反方向从地板中钻出来。显然,这样的事情是很荒唐的,在现实世界中不可能发生。但如果不去刻意避免,这种荒唐事在仿真中的的确确会发生。
这个问题是一个典型的系统状态不连贯问题,产生的原因,是由于由数学模型到仿真程序的过程中的连续时间离散化。
由于由数学模型到仿真程序的过程中必须对连续时间离散化,只要存在系统状态不连贯,在仿真中必然会有相应的系统状态不连贯问题。
这些由数学模型到仿真程序过程中出现的问题,是需要通过模型校核来发现并解决的问题。
3 系统状态不连贯问题的已有解决方法
由上述可知,产生系统状态不连贯问题的根本原因是在仿真中将连续时间离散化了,从而不能在发生系统状态不连贯的瞬时产生正确的仿真行为,并产生后续影响。基于此,自然会想到,解决系统状态不连贯问题需要确定发生系统状态不连贯的瞬时,并使得某个仿真时间点与该瞬时重合。但是,由于时间具有严格数学意义上的连续性,要预先确定现实世界中某个事件发生的精确时刻在理论上是不可能的,在仿真中要使得某个仿真时间点与该精确时刻重合更是不可能的。因此,解决系统状态不连贯问题的关键是以要求的精确度检测到系统状态不连贯的发生,即确定系统状态不连贯发生的瞬时(称为近似瞬时),并以该近似瞬时为节点进行相应的状态转换。目前已有的确定近似瞬时的方法可以归纳为三种。
3.1 确定近似瞬时的方法1
确定近似瞬时的具体方法1用于变步长仿真。
对于一些系统状态不连贯,可以在仿真程序中设计不连贯特征变量,使得当系统状态远离不连贯点时该变量的变化较慢,而当系统状态接近且趋向不连贯点时,该变量快速变化。在变步长仿真中,解算器可以根据需要动态调整仿真步长。因此,可以让解算器对不连贯特征变量进行监测,当其慢变化时增加仿真步长以加快仿真速度,当其快变化时减小仿真步长,以要求的精确度命中系统状态不连贯的发生时刻。这种方法在本文中称为不连贯特征变量变化率检测方法,简称为变化率检测方法。
变化率检测方法存在以下缺陷:
1)对仿真步长的减小是盲目的,因为是不连贯特征变量快速变化不一定会产生系统状态不连贯;
2)为确定近似瞬时,解算器必须额外进行很多短的仿真时间步上的计算,这将极大地降低仿真速度。要求的精确度越高,额外计算就越多,仿真速度的降低就越严重;
3)并不是对任意的系统状态不连贯都能够设计不连贯特征变量。
3.2 确定近似瞬时的方法2
确定近似瞬时的方法2用于固定步长仿真。
固定步长仿真中的解算器在固定的最小步长的整数倍时间点上进行仿真解算。为确定近似瞬时,可以降低固定的最小步长。这将极大地增加仿真的执行时间。
3.3 确定近似瞬时的具体方法3
确定近似瞬时的方法 3是所谓的零跨过检测(zero-crossing detection)方法。该方法在 MATLASimulink中采用。
零跨过检测方法实施过程如下:在仿真程序中登记了一个零跨过变量的集合,每一个零跨过变量是一个可能产生不连贯的系统状态的函数(称为零跨过函数)。当系统状态不连贯发生时,相应的零跨过函数会改变符号(即跨过 0值)。在每一个仿真时间步的最后时刻,Simulink将更新零跨过变量,并且检测从上一个仿真时间步到当前是否有零跨过变量跨过 0值(即发生零跨过)。如果有,就表明在当前的仿真时间步中发生了一个不连贯。
如果有零跨过被检测到,Simulink将通过插值来估计零跨过发生的时刻。这样,Simulink就能够以要求的精确度确定近似瞬时。
零跨过检测使得Simulink能够精确地对不连贯进行检测而不必求助于过小的仿真步长。这使得可以对包括有系统状态不连贯的系统,进行快速而精确的仿真。
显然,零跨过检测方法是一种回溯的方法,这种方法有以下优点:1)只在真正发生系统不连贯的时候才进行插值计算,避免了方法 1中的盲目性;2)只需要在零跨过发生的仿真时间步中进行插值,避免了方法 1中可能会发生的大量的额外计算;3)对任意的系统状态不连贯都能够方便地设计和使用零跨过变量。
零跨过检测方法对于方法1有很大的改进。但是,零跨过检测方法也有以下一些缺点:1)只能用于变步长仿真;2)在系统状态不连贯频繁发生的情况下会失效,并导致仿真停止;3)零跨过有可能被漏检。
关于零跨过有可能被漏检的问题做如下说明。
在变步长仿真中,仿真步长通常由误差容忍度和系统的运行情况来确定。误差容忍度大会导致仿真步长大,就有可能检测不出一个已经发生的零跨过。例如,如果零跨过发生在一个仿真时间步里,但是在该仿真时间步的开始时刻和最后时刻,对应的零跨过变量没有指示符号变化,Simulink就检测不出该零跨过。
如图2所示,给出了同一个零跨过变量在不同仿真步长下的两种可能情况。该零跨过变量分别在t1时刻和时刻t2发生了零跨过。图中的圆点对应的横轴值是仿真时间点。在第一种情况(仿真步长较长),两次零跨过都没有被检测出来,因为在对应的仿真时间步的开始时刻和最后时刻,零跨过变量的符号没有变化;而在第二种情况(仿真步长较短),两次零跨过都能够被检测出来。
第一种情况下发生的零跨过漏检不可能通过零跨过检测机制本身来发现和纠正。在零跨过检测机制下,要避免零跨过漏检,只能靠普遍地强制减小仿真步长,这导致了另外一种意义上的盲目性,也降低了仿真效率,在很大程度上抵消了零跨过检测机制的优势。

图2 零跨过漏检说明图
4 反舰导弹仿真中的目标命中判断问题
4.1 目标命中判断问题的描述
在笔者已经完成的一个反舰导弹电子干扰攻防对抗仿真系统[7](以下也简称为本仿真系统)中,对反舰导弹进行了基于仿真目的的全系统、六个自由度、全弹道的仿真;对目标舰艇进行了电磁学、运动学和目标舰体等三个方面的仿真。运动学方面的仿真涉及目标舰艇在海平面上的位置、运动速度、运动方向及舰艏方向等;目标舰体涉及目标舰艇的长度 LS、宽度WS、吃水 HSB和干舷 HSA。目标舰体用其长度、宽度和总高度围成的六面体(称为舰体六面体)来表征。
为简化问题,在本仿真系统中有一个基本假设:认为反舰导弹攻击水面舰艇目标时,在空中、水中和目标舰体中有相同的运动速度 V(包括数值和方向),即忽略海水和目标舰体对反舰导弹速度的影响。从本仿真系统的仿真目的出发,这个假设是可以接受的。
本仿真系统中的目标命中判断模型相关要点如下:1)以反舰导弹发射点为原点,建立东北天大地坐标系 GC;2)反舰导弹位置由其质心在 GC中的坐标XMGC、YMGC和ZMGC表征;3)目标舰艇位置由其几何中心在GC中的坐标XSGC、 YSGC和ZSGC表征;4)以目标舰艇的几何中心为原点、指向舰艏的水平方向为X轴正向,向上为Z轴正向,按右手定则确定的目标舰艇宽度方向为Y轴正向,建立目标舰体坐标系SC;5)将反舰导弹质心的GC坐标转换为SC坐标XMSC、YMSC和 ZMSC;6)如果在某一瞬时反舰导弹的质心进入舰体六面体,则做出反舰导弹命中目标的判断。当满足下式时,认为反舰导弹的质心进入舰体六面体:

该目标命中判断模型可以用于要求直接命中的弹药的目标命中判断。水面舰艇的舰艏部分和主甲板以上的部分与规则的矩形有较大的差异,如果仿真中反舰导弹命中的是这些部位,则可能会与实际的命中情况有一些偏差。因此,在应用上述模型时,需要对具体的命中部位进行分析。
4.2 目标命中判断问题是一个系统状态不连贯问题
本仿真系统采用的是固定步长,对反舰导弹的仿真步长是 1ms(ms量级的仿真步长对于全系统、六个自由度、全弹道的反舰导弹仿真是必需的),对目标舰艇的运动学仿真的仿真步长也取为1ms。
在 1ms的仿真步长下,按照上述的目标命中判断模型,在每次仿真中都能够正确判断反舰导弹是否命中目标舰艇。但是,当将本仿真系统中产生的反舰导弹质心以及目标舰艇几何中心的大地坐标系坐标送到上层仿真系统,在反舰导弹实际命中目标舰艇的情况下,上层仿真系统几乎总是给出反舰导弹未命中目标而入水的判断结论。问题出在哪里呢?上层仿真系统采用的目标命中判断模型与本仿真系统相同,不同的是其仿真步长为20ms。
由于反舰导弹在接近目标舰艇时采取俯冲弹道,其在水下的运动轨迹(设为一条直线)会与水面有一个角度。反舰导弹与水面舰艇的交会可用图3示意说明。
图3中,水平线表示海平面;纸面表示一个铅垂面;目标舰艇艏艉线与纸面垂直,矩形表示水面舰艇向纸面的投影,矩形的宽度即为水面舰艇的宽度,矩形在海平面下的高度即为水面舰艇的吃水;反舰导弹攻击目标舰艇时的运动轨迹是在纸面上的一条直线。

图3 反舰导弹与水面舰艇交会示意图
图3中示出了除仿真步长不同外完全相同的两种情况。左边部分的仿真步长为 20ms;右边部分的仿真步长为 1ms。图中还标出了在各个仿真时间点反舰导弹的位置:t11和 t12表示第一种情况的第一和第二个仿真时间点;t2n表示第二种情况的第n个仿真时间点,n=1,2,…21,t11=t21=t1以及t12=t221。
两种情况下,反舰导弹在相同的时刻t1到达相同的位置,在这个位置上,反舰导弹已经接近但尚未命中目标舰艇。随后,反舰导弹以相同的速度继续沿相同的原方向运动。对于第二种情况,在时刻t1后的下一个仿真时间点t22,反舰导弹即进入舰体六面体,因此判断反舰导弹命中目标舰艇。这是一个正确的结论。对于第一种情况,在时刻t1后的下一个仿真时间点t12,反舰导弹所运动到的位置仍然在舰体六面体外面,因此判断没有命中目标舰艇,而在这以后反舰导弹不可能再进入舰体六面体了。最后得出错误结论:反舰导弹没有命中目标。
上述过程中,反舰导弹由舰体六面体外到内发生了一个系统状态不连贯,再由舰体六面体内离开到舰体六面体外则发生了又一个系统状态不连贯,如果这两个系统状态不连贯在一个仿真时间步中相继发生,则由于在这个仿真时间步的开始时间点和结束时间点上相应的系统状态没有改变,即反舰导弹都处于舰体六面体外,如果应用 Simulink的零跨过检测方法,就会发生图2所示的零跨过被漏检的错误,也就不能正确判断反舰导弹对目标舰艇的命中。
5 解决系统状态不连贯问题的新方法—预测法
对于上述的目标命中判断问题以及其它的一些系统状态不连贯问题,变化率检测方法和零跨过检测方法都可能失效,采用固定的非常小的仿真步长在很多情况下会大大降低仿真效率,因而也不可取。因此,提出一种称作预测法的解决系统状态不连贯问题的方法。
预测法包含以下要点:
1)基于对系统本身的分析,确定最小仿真步长Δtmin。Δtmin取决于两个因素,一是要求的仿真精度对应的最小仿真步长(记作ΔtPmin),二是会发生不连贯的系统状态的各种取值的持续时间中的最小值(记作ΔtBmin)。要求:
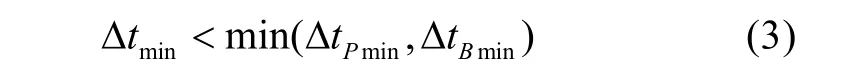
2)在每一个仿真时间步(仿真步长为ctΔ)的最后时刻(记作nt),按ctΔ预测在下一个仿真时间步中是否会发生系统状态不连贯。
3)如果在下一个仿真时间步中会发生系统状态不连贯,则估计其发生时刻/t,对于估计误差tδ,要求:

4)如果 t/-tn≤Δtmin,则以Δtmin为仿真步长,进行下一步的仿真;如果没有发生系统状态不连贯,则仍以Δtmin为仿真步长,进行再下一步的仿真。因为有(4)式以及对Δtmin的要求,在下一步或者再下一步的仿真中,预测到的系统状态不连贯必然会发生并且以要求的仿真精确度被检测到。
5)如果t/-tn>Δtmin,则以t/-tn-为仿真步长,进行下一步的仿真。在这一步中,系统状态不连贯肯定不会发生。然后以Δtmin为仿真步长,进行再下一步的仿真。在这一步中,系统状态不连贯肯定会发生。这样,预测到的系统状态不连贯必然以要求的仿真精确度被检测到。
6 预测法用于解决目标命中判断问题
预测法的要点中的(4)和(5)是容易实现的程序性步骤,而在要点(2)中已经涵盖了(3),这里主要阐述前面二个要点。
6.1 确定最小仿真步长mintΔ
在上层仿真系统中,ΔtPmin= 20ms。
为确定ΔtBmin,将反舰导弹与水面舰艇交会的情况重绘于图4,图中的A、B是反舰导弹运动轨迹与舰体六面体的两个交点。

图4 用于确定minBtΔ的反舰导弹与水面舰艇交会示意图
由基本假设和图3等可知,反舰导弹攻击目标时,处于目标舰体中的时间最短,这个时间(记作Δt)的最小值就是ΔtBmin。目标舰艇的吃水、反舰导弹运动轨迹所在铅垂平面与目标舰艇艏艉线的夹角φ、该运动轨迹与水面的夹角θ(最大值为θmax)以及反舰导弹命中点(即图 4中的 A 点)的深度 Y0(最大值为Y0max),都影响Δt。对于吃水一定的目标舰艇,当满足以下条件时Δt达到ΔtBmin:
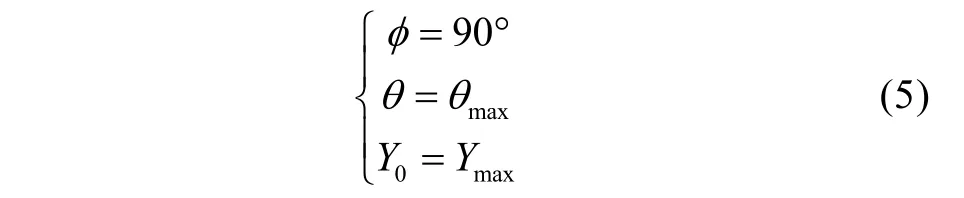
因此,对于minBtΔ,有:
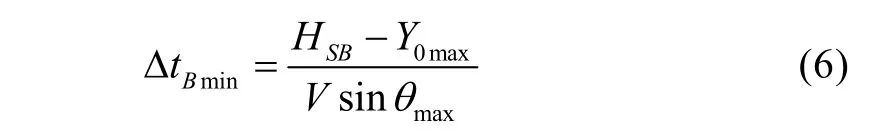
将具体数据代入后,有ΔtBmin<ΔtPmin,按照式(3)可得Δtmin= 4ms 。
6.2 预测在下一个仿真时间步中的系统状态不连贯
在所论问题中,预测在下一个仿真时间步中的系统状态不连贯包括两个步骤:首先要确认反舰导弹运动轨迹是否会与舰体六面体的前、后、左、右四个面中的某个面相交,在一次仿真中,这个步骤仅需进行一次;如果会与某个面相交,则需在每一个仿真时间步都确认相交时刻是否会发生在下一个仿真时间步中。
本文给出判断反舰导弹运动轨迹(以下也简称为运动轨迹)是否会与舰体六面体的左面相交的算法要点:
1)获得运动轨迹上的两个点在舰艇坐标系中的坐标;
2)这两个点确定一条直线L,得到运动轨迹直线在舰艇坐标系中的表达式(例如,参数式):
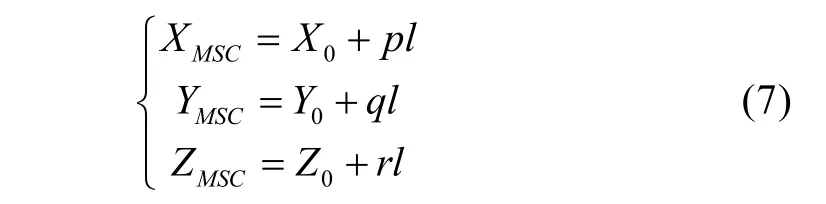
式中,(X0,Y0,Z0)是直线L上的一个点,p、q、r是L的方向数。
3)舰体六面体的左面上的点在舰艇坐标系上满足如下条件:
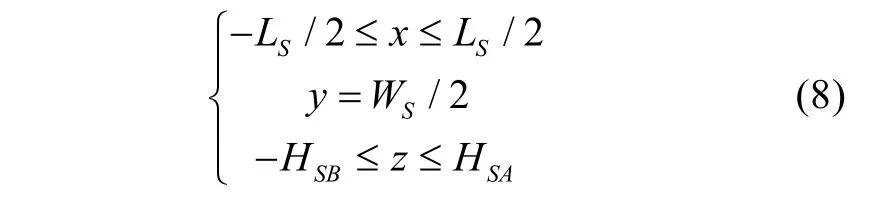
4)令式(7)中的YMSC= YMSC0=WS/2,求出 l;将 l代入式(7)中的第一式和第三式,求出相应的x和z坐标(XMSC0和ZMSC0),如果其分别满足式(8)中的第一式和第三式,则该点就是反舰导弹运动轨迹与舰体六面体的左面相交的交点,否则反舰导弹运动轨迹与舰体六面体的左面不相交。
得到反舰导弹运动轨迹与舰体六面体的左面相交的交点后,就可以确认相交时刻是否会发生在下一个仿真时间步中,要点如下:
1)求本仿真时间步的最后时刻反舰导弹所在点与交点的距离;
2)该距离除以反舰导弹运动速度 V,得到相应的运动时间T;
3)若下一个仿真步长≥T,则相交时刻发生在下一个仿真时间步中。
7 结束语
系统状态不连贯在现实世界中是普遍存在的,客观地认识并在仿真中解决相关的问题,对于保证由数学模型到仿真程序的正确转换,进而保证仿真的真实,是非常必要的。
相对于已有的方法,本文提出的解决系统状态不连贯问题的预测法具有以下几个方面的优势:
1)通过对系统状态不连贯的预测,避免了处理系统状态不连贯的盲目性;
2)通过确定最小仿真步长mintΔ,避免了对系统状态不连贯的漏检;
3)有很高的计算效率,最多进行两步最小步长仿真,就能够以要求的精确度检测到任何一个系统状态不连贯;
4)可以用于变步长仿真,也可以用于固定步长仿真。
当然,作为一种新方法,预测法肯定还会存在一些缺点和缺陷,并有待于进一步完善。
[1]孙勇成.M&S的相关 VV&A技术研究[D].南京:南京理工大学,2005.
[2]徐庚保,曾莲芝.关于建模与仿真的可信性问题[J].计算机仿真,2003, 20(8):36-38.
[3]郑利平.仿真 VV&A 分析和管理方法研究[D].合肥:合肥工业大学,2007.
[4]王维平,朱一凡,华雪倩,等.仿真模型有效性确认与验证[M].长沙:国防科技大学出版社,1998.
[5]王正中. 系统仿真技术[M].北京:科学出版社,1986.
[6]程卫国,冯峰,王雪梅,等. MATLAB5.3 精要,编程及高级应用[M].北京:机械工业出版社,2000.
[7]邱杰,孙迎丰.反舰导弹电子干扰仿真系统研究[J].系统仿真学报,2008,20(4):267-270,274.

