小型电加热反应器温度的RBF神经网络自整定PID控制

于蒙，邹志云，赵丹丹，王志甄，盖希杰

（防化研究院，北京102205）

小型电加热反应器被广泛应用于化工实验，其准确的温度控制对化工实验的顺利进行至关重要。一般选择常规PID控制方法控温，但常规PID控制在设定温度下需要通过整定算法整定出合适的控制参数，电加热反应过程滞后较大，整定过程耗时较长，如常采用的基于Ziegler－Nichols PID整定算法一般需耗时2～4h。由于其非线性和时变性，若换一个设定温度或是在反应物容量、实验环境等条件变化时，整定出的参数值就会不适合，就需要重新整定参数［1］。因此，一种能够自整定参数的控制算法对这种小型电加热反应器的温度控制显得十分重要。

神经网络与PID控制相结合在控制领域一直是热点，利用神经网络来辨识非线性系统的模型，从而对PID的参数进行优化［2］。径向基函数RBF（Radial Basis Function）神经网络是一种具有单隐层的三层前馈神经网络，它模拟了人脑神经网络中局部调整、相互覆盖接受域的特点，是一种局部逼近网络［3］。很多文章论述了采用RBF神经网络辨识非线性系统的模型从而自适应整定PID参数的方法，但大部分研究成果停留在仿真阶段，通过选择低阶纯滞后模型来验证这种算法的有效性［4－8］。笔者则将基于RBF神经网络的自适应PID算法应用于小型电加热反应器的温度控制实验。在工控机上用组态软件对小型电加热反应器进行数据采集和过程监控，应用动态数据交换DDE（Dynamic Data Exchange）实现组态软件与Matlab的实时数据通信；把组态软件采集的实时数据送到Matlab中，用Matlab进行PID参数的自适应整定，实现小型电加热反应器基于RBF神经网络的自适应PID控制。

1 电加热反应器

小批量化工产品生产中经常用到的小型电加热反应器系统组成如图1所示［1］。装置由玻璃三口瓶、单相电热套、温控箱、PT100铂热电阻组成。控制系统由S7－200控制器和工业控制计算机组成。

小型电加热反应器温控的工作原理：分度号为Pt100的铂热电阻测量反应溶液的温度，将该温度信号送至S7－200的EM231模拟量输入模块，CPU226进行采集后，通过 RS－485／RS－232转换器送到工业控制计算机中的“组态王”中进行显示、记录，“组态王”用DDE方法将数据送至Matlab中，进行基于RBF神经网络的自适应整定PID控制运算，运算后输出值再用DDE送至“组态王”，最终由EM232输出4～20mA的电流信号。该信号经单相调压板PAC15和双向可控硅MTC调节加热电压。温度低于设定温度时加大电压，温度高时降低加热电压，使加热温度保持恒定。

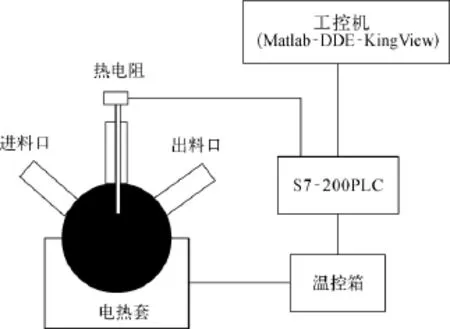
图1 小型电加热反应器及其控制系统示意

2 基于RBF神经网络的自适应PID控制

基于RBF神经网络的自适应PID控制结构如图2所示，其中x1，x2，x3为控制器的3个输入，分别为e（k）－e（k－1），e（k），e（k）－2e（k－1）＋e（k－2）；K 为增益因子［9］。

假设要修正的增量式PID控制中的k时刻权值为wj（k），j＝p，i，d，下一时刻的权值调节公式为

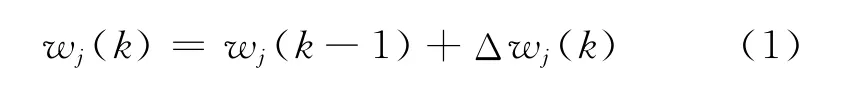
式中：Δwj（k）——权值增量。引入输出误差平方函数作为性能指标，即：

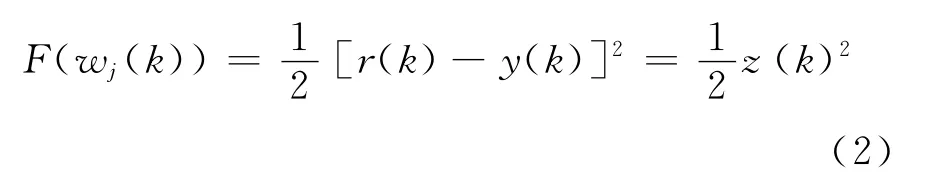
式中：r（k），y（k）——参考输入和输出。权值修正量为

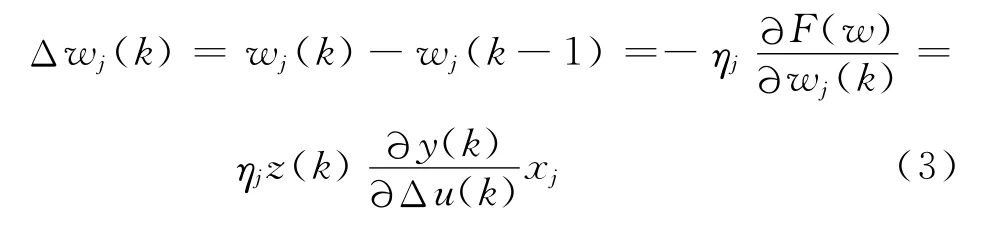
式中：ηj——学习速率，j＝p，i，d。为了得到精确的∂y（k）／∂Δu（k）值，在控制增量权值调整环节 引 入 RBF 网 络，对 ∂y（k）／∂Δu（k）进 行辨识［10］。

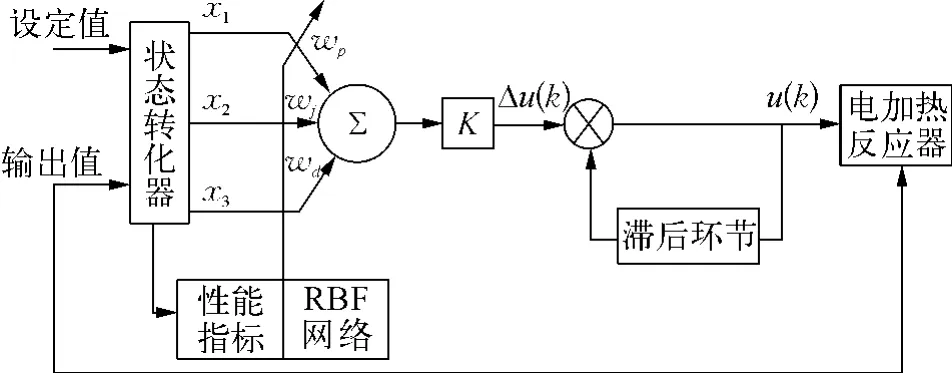
图2 基于RBF神经网络的自适应PID控制结构

RBF网络拓扑结构如图3所示。在RBF网络结构中，X＝ ［x1，x2，…，xn］T为网络的输入向量，n为输入层神经元个数；隐含层径向基向量H ＝ ［h1，h2，…，hj，…，hm］T，其中hj为高斯函数，m为隐含层神经元个数。

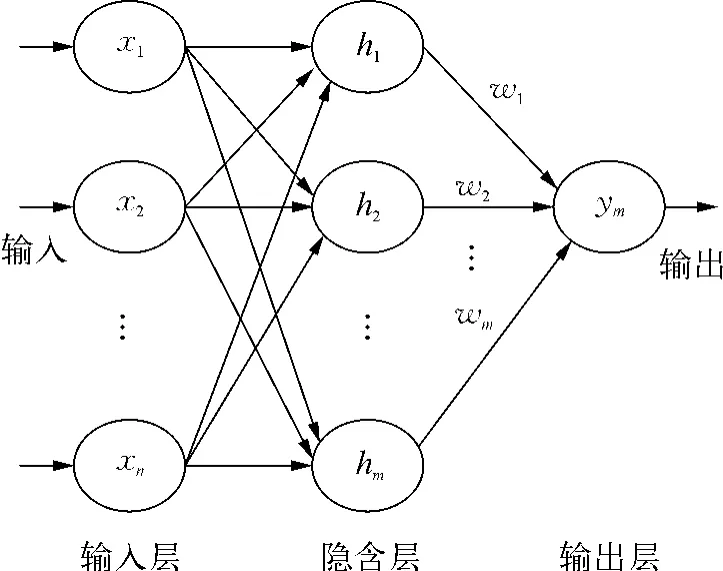
图3 RBF神经网络拓扑结构

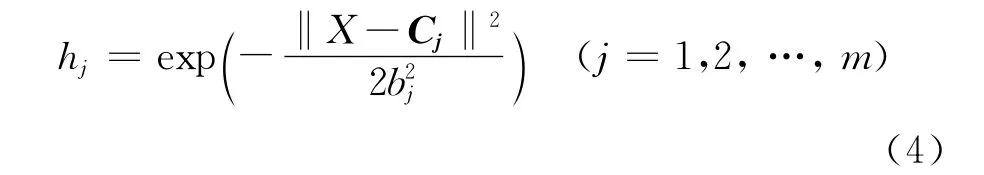
式中：Cj——RBF神经网络隐含层第j个节点的中 心 矢 量；Cj＝ ［c1j，c2j，…，cij，…，cnj］T；bj——隐含层节点j的基宽度参数，且为大于零的数；RBF神经网络隐含层节点基宽向量B＝［b1，b2，…，bj，…，bn］T。

网络的权向量为w＝ ［w1，w2，…，wj，…，wm］，辨识网络的输出为ym（k）＝w h ＝w1h1＋w2h2＋…＋wmhm。辨识网络输出权值由下式决定：

式中：α——动量因子；β——学习因子。

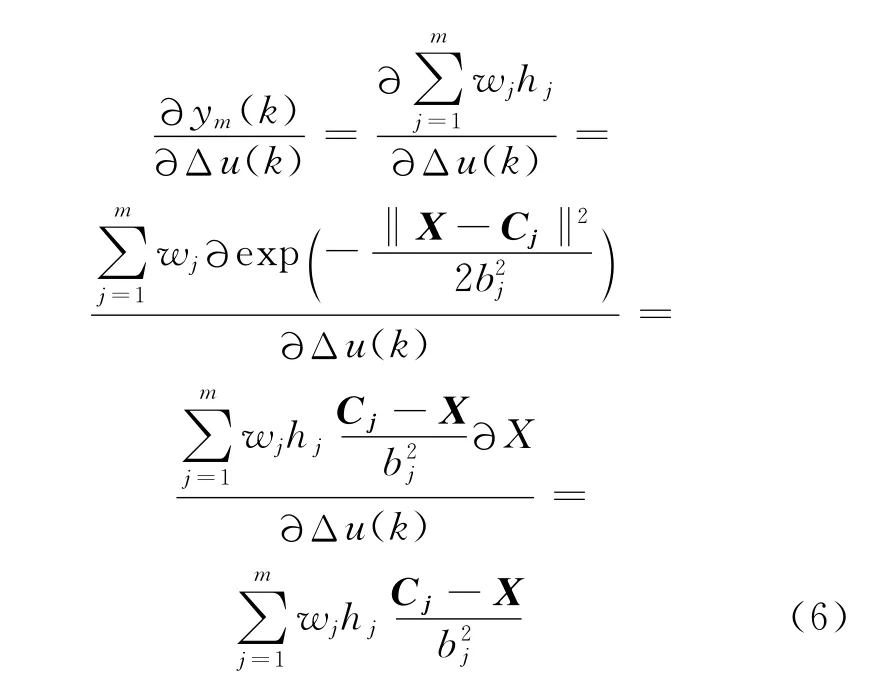
采用梯度下降法，迭代计算节点中心矢量和节点基宽参数：

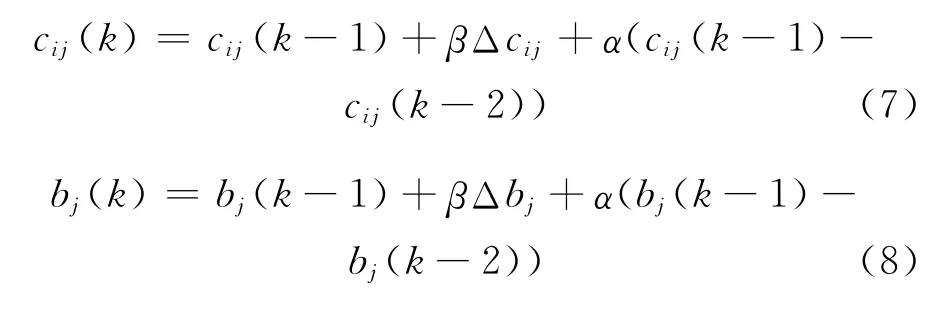
3 算法的实现

在Matlab中实现基于RBF神经网络的自适应PID控制算法时，需先在“组态王”中定义好Matlab需要用到的DDE传送的过程变量，定义形式是“过程变量（连接设备.寄存器）”。这些变量包括经EM231模拟量输入模块采集到的温度测量值（S7200.V100）、温度的设定值（S7200.V128）和遥控EM232模拟量输出模块输出的控制量（S7200.V110）等。Matlab与“组态王”的DDE连接主要包括几个函数：如通过ddeinit（‘View’，‘TAGNAME’）命令进行 Matlab和“组态王”的DDE通信初始化；利用ddereq（channel，‘S7200，V100’）命令获取“组态王”中的现场温度变量存储的温度值；使用ddepoke（channel，‘S7200.V110’，u（k））命令将运算后的输出值传输给“组态王”输出控制变量。

Matlab与“组态王”通信建立后，基于RBF神经网络的自适应PID程序就可周期性地获取来自“组态王”的现场温度数据和设定值数据，进行PID参数的整定，得到整定值的增量，并用kP＝kP0＋ΔkP，kI＝kI0＋ΔkI，kD＝kD0＋ΔkD计算本次循环的kP，kI和kD的整定值。利用在每次循环中新得到的kP，kI和kD的整定值，按增量式PID控制算法计算控制输出量，再通过DDE将结果传输给“组态王”。

程序的流程如图4所示，其主要工作流程为定义全局变量、Matlab与KingView的DDE通信初始化，判断通信是否成功，如不成功则显示“DDE通信失败”；如成功，则显示“DDE通信成功”。引入For循环，并设定循环次数，每次循环Matlab从KingView获取过程变量和设定值，通过基于RBF神经网络的PID算法整定PID参数；用增量式PID算式计算控制输出，对输出进行限幅，然后输出控制作用；绘制过程变量曲线图，存储过程数据文件，终止DDE通信。

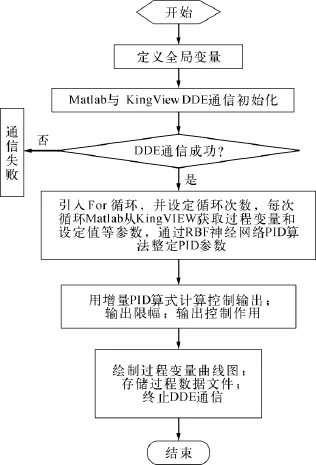
图4 基于RBF神经网络的自适应PID程序流程

4 温度控制实验

使用一套功率为500W的小型电加热反应器验证基于RBF神经网络的自适应PID控制的有效性，并将这种控制策略与常规PID进行对比。

基于RBF神经网络的自适应PID控制原理与方法上一节已经说明，其控制中枢在工控机，通过Matlab与“组态王”结合实现算法，S7－200控制器起到获取现场温度模拟信号和输出控制模拟信号的作用。常规PID控制中枢在S7－200控制器，在STEP7编程软件中，利用PID编程向导生成一个PID模块，针对每个设定温度预先设定初始参数，再利用PID控制调谐面板整定设定温度下的PID参数值。调谐面板的参数整定采用的方法是Ziegler－Nichols整定方法，通过改变输出值，使设定值曲线与现场温度曲线产生相交事件。这种整定方法，振荡幅度较大，振荡时间较长，需要完成12次零相交事件，自整定才会送出计算值，整个整定过程要耗时4h左右。

小型电加热反应器的三口烧瓶中装入4L液体，分别用两种控制方法对其进行加热。基于RBF神经网络的自适应PID控制采用一套参数（α＝0.05，β＝0.5，初始权值kP0＝6.8，kI0＝0.016，kD0＝0；ηP＝1 200，ηI＝1.8，ηD＝0），常规PID在设定温度为60℃时整定出一组控制参数（增益7.215，积分时间8.952min，微分时间0）。常规PID控制整定过程如图5所示，可以看出现场温度曲线与设定值曲线完成了12次相交事件。图6为设定温度为60℃控制效果图，可以看出两种控制策略在上升时间与稳定时间相近，但基于RBF神经网络的自适应PID没有出现超调，而常规PID参数出现了2.1℃的超调，也可看出常规PID波动幅度稍大。

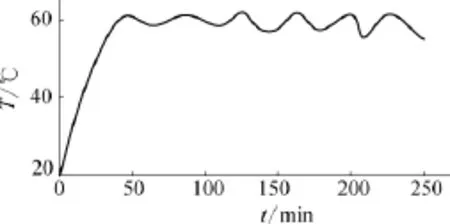
图5 常规PID控制设定温度60℃时整定过程

将烧瓶中液体量减少到3.5L时，两种控制策略参数不变，控制效果如图7所示。

可以看出基于RBF神经网路的自适应PID控制无论在上升时间还是在控制精度上都要优于常规PID控制。液体量发生变化后，常规PID控制之前整定出的参数已经不适合当前加热状态，最终现场检测温度与设定温度有了2.7℃的误差。

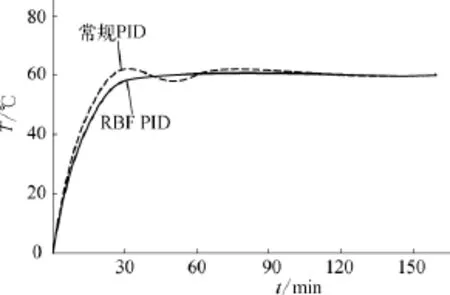
图6 设定温度为60℃时两种控制策略比较

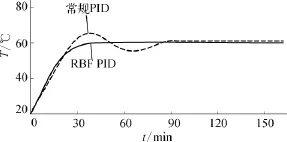
图7 液体量减少为3.5L时两种控制策略的比较

烧瓶中液体量恢复为4L，设定温度变为40℃，80℃时，两种控制策略的控制效果对比如图8，图9所示。

图8 设定温为40℃时两种控制策略的比较

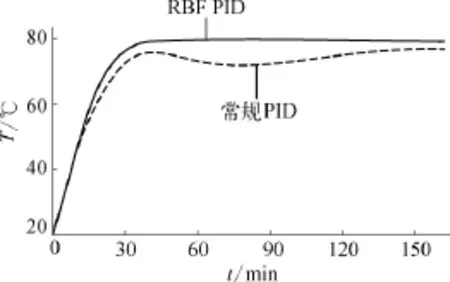
图9 设定温为80℃时两种控制策略的比较

设定温度变化后，基于RBF神经网络的PID控制会自适应调整权值参数，可以看出无论温度上升为80℃还是下降为40℃，现场温度都可以快速、准确地达到并保持在设定温度。常规PID控制在设定温度发生变化后，原控制参数已经无法胜任当前的控制要求。设定温度为40℃时，现场检测温度达到了37.6℃，低设定温度2.4℃。设定温度为80℃时，现场温度始终没有达到设定温度，最终稳定在78.1℃。

在设定温度为80℃时，基于RBF神经网络的自适应PID控制的参数调整情况如图10，图11所示，可以看出RBF神经网络实现了PID参数的自适应整定，最终将比例和积分参数稳定在6.878，0.013 2。

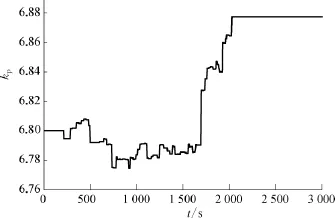
图10 基于RBF神经网络的自适应PID控制比例参数调整示意

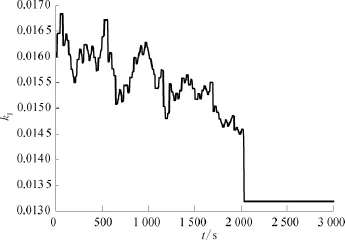
图11 基于RBF神经网络的自适应PID控制积分参数调整示意

5 结束语

常规PID控制算法中的比例、微分、积分参数在运行初期设定后便固定不变，不具备自学习、自适应能力。对于具有非线性、大滞后和时变特性的电加热温度控制，采用传统PID的温度控制适应性和鲁棒性差，控制性能有待提高。文中将基于RBF神经网络的自适应PID控制应用于小型电加热反应器的温度控制，并将其与常规PID控制进行比较。实验结果表明，基于RBF的神经网络的PID控制通过在线辨识建立了过程模型并为参数整定提供了梯度信息，达到了在线辨识与在线控制的目的，且控制精度高，动态性能好，具有较好的自适应性和鲁棒性。

［1］邹志云，赵丹丹.小型电加热反应器温度的模糊自适应整定PID控制［J］.计算机与应用化学，2009，26（08）：56－58.

［2］李国勇.智能控制及其Matlab实现［M］.北京：电子工业出版社，2010：24－29.

［3］MENG Joo，ER Shiqian，WU Juwei，et al.Recognization with Radial Basis Function（RBF）Neural Network［J］.IEEE Trans on Neural Networks，2002，13（03）：697－710.

［4］赵为光，杨莹.电锅炉温度控制系统PID参数整定算法的改进［J］.工业仪表与自动化装置，2009，5（01）：87－90.

［5］李云娟，方彦军.一种RBF神经网络自适应PID控制器在超临界温度系统的应用研究［J］.控制理论与应用，2010，29（11）：1－3.

［6］张明光，王兆刚.基于RBFNN在线辨识的自适应PID预焙阳极焙烧炉温度控制［J］.有色金属，2008，4（01）：20－23.

［7］王杰，姜国强，王栓.基于混合学习算法的RBF神经网络主蒸汽温度控制［J］.热力发电，2009，38（02）：78－83.

［8］李小凡.基于RBF神经网络整定的PID控制器设计［J］.兵工自动化，2009，28（01）：45－50.

［9］孙增圻.智能控制理论与技术［M］.北京：清华大学出版社，2000：125－137.

［10］刘金琨.智能控制［M］.北京：电子工业出版社，2005.