全钒液流电池双极板流道的建模及其优化

刘 记，左春柽，于海明，2，左雨欣，张 昭，刘 鹏

（1.吉林大学机械科学与工程学院，吉林 长春 130025；2.黑龙江八一农垦大学工程学院，黑龙江 大庆 163319）

能源是社会发展与经济增长的最基本驱动力，是人类赖以生存的重要物质基础。人类社会发展过程中使用了大量的化石能源，特别是自工业革命以来，大量的石油被利用，不仅导致温室气体和环境污染物排放量持续增加，而且这些能源也面临枯竭的危机，能源可持续发展成为举世瞩目的社会课题。为了实现可持续发展社会目标，必须研究开发绿色无污染的发电技术，如风能、太阳能、潮汐能等。然而，可再生能源发电过程受气象条件影响明显，具有随机性、不连续性特征，难于作为持续稳定的电源使用[1]。因此，无论是哪种能源的利用，都需要高性能的储能系统与之匹配，能够将富余的电能存储起来，以待电力缺乏时使用，还能够实现给边远地区供电，以及解决电网调峰的问题。另外，电动交通工具的发展以及农业上大马力拖拉机也需要具有高性能的储能系统。钒氧化还原液流电池，由于具有造价较低，使用寿命长，无毒，有利于环保、功率和容量可以灵活改变、可以100%深度放电，而且无需保护和保存期无限，储存寿命长等优点，成为储能的最佳选择之[2]。全钒氧化还原液流电池（VRB）的研究最早始于澳大利亚新南威尔士大学（UNSW）Skyllas-kazacos 研究小组[3]，经过几年的发展，全钒氧化还原液流电池开始走出实验室，并迈向工程化研发阶段。

在全钒液流电池中，双极板是全钒液流电池的关键部件之一，起着连接不同单电池的正负极并导通电池内电路的作用，要求其具备良好的导电性、机械强度、耐化学氧化和电化学腐蚀性能。目前，国内外的专家学者主要从材料对电池性能影响等方面对双极板进行研究，并取得了很大的成就，但是有关双极板流道优化方面的报道较少，并且这方面对液流电池的性能有很大影响，因此，对双极板流道进行优化设计具有非常重要的意义。由于在传统的两种平直并联流道和蛇形流道中，平直并联流道具有电解液的流程较短、流动阻力较小，电解液分布不均匀等缺点，影响了电池的性能；而蛇形流道虽然电解液分布均匀，但是其流程较长，流动阻力较大，也对电池性能产生不利影响。因此，本文将在平直并联流道的基础上，对流道结构进行两次优化，确定出最佳的流道结构，为全钒燃料电池的设计和生产提供理论基础。

1 数值模型

本文采用传统的平直并联流道结构，如图1 所示，在此基础上对其流道结构进行优化。该结构的具体尺寸见表1，压差使电解液以层流状态在流道内流动，氧化还原反应在膜的两侧同时放生，在充放电时，阴阳极发生的电化学反应如下[4~5]：

正极电解液的反应方程为：

负极电解液的反应方程：

全钒液流电池的总化学反应方程式：

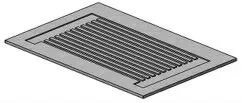
图1 平直并联流道

表1 双极板几何尺寸（mm）

1.1 控制方程

本文假设全钒溶液为不可压缩流体，不考虑重力对流体流动的影响，当不可压缩流体在流道中低速流动时，其雷诺数很小，钒溶液在流道内以层流的状态流动，相应流体的连续方程和动量方程为

式中，

u 为流体平均速度矢量；

p 为流体压力；

ρ 和μ 分别为流体的质量密度和动力粘度。

1.2 计算模型

在并联式电池电堆中，流体从入口总管进入若干个平行的单电池，然后在出口总管处汇集流出。流体的流动相当于穿过若干个串并联的流阻。R.J.Boersma 等人认为，这种电堆的流体模型可以描述为一个液压阻力网络[6]，如图2 所示。

图2 并联式液压阻力网络

可以设想把流体入口总流道与出口总流道切割成若干小段，流体入口总流道各小段的阻力系数为K1，出口总流道个小段的阻力系数为K2，各支流道内的液压阻力为Kc。j 支流道内的流量为Qj，其进出口压力分别为p1j与p2j。由于全钒液流电池双极板流道内的流动状态为层流，支流道内的压降公式可以表示为：

式中，Q 为支流道内的流量。在总流道中入口与出口处的两个相邻支流道之间的压降，分别为△pin与△pout，它们的表达式为：

式中，Qi与Qo分别为入口总流道与出口总流道处的流量。

在图2 中，符号的下标表示支流道的个数。所有支流道的形状与尺寸均相同。根据公式（6）、（7）和（8）可得通过支流道j 的压降：

在图2 中，大多数误差存在阻力网络的顶部，除了最上面的支流道外，所有支流道的K1与K2都可以假设是常数，假设流量的分布比较均匀。那么，可以用从j 到n 的所有支流道的平均流量Q 代替Qi。所以，公式（9）将变为：

由液压阻力网络图2，可知：

结合公式（10）与（11），可得：

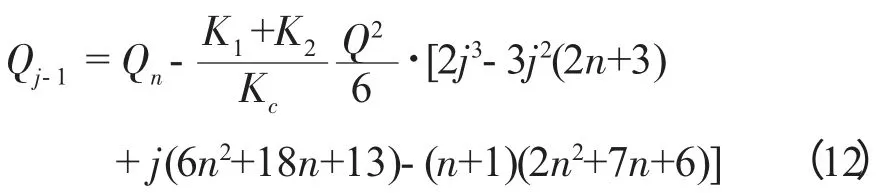
假设支流道J 内的流量是整个平直并联流道的平均流量，则：

将公式（12）代入上式，得：

支流道J 内的流度为：

AJ为支流道的面积，AJ=b×h（b 是槽宽，h 是槽深）。

1.3 边界条件

利用商业CFD 软件FLUENT 对上述数学模型进行求解，在Gambit 中，进行网格划分。为了提高网格品质，采用分块结构化网格。边界条件的选择为速度入口（Velocity inlet）、压力出口（Pressure outlet）与无滑移的标准壁面（wall）。入口边界条件是速度入口，入口速度设为：ν=0.01 m/s；出口边界条件为压力出口，表压强（Gauge Pressure）设为pgauge=0 atm；其余边界条件均设为wall。

2 结果与讨论

在模拟计算中，首先对传统平直并联流道内的流体进行数值模拟，研究其速度分布图，根据所反映出来的问题，对传统平直并联流道两次优化，最终确定流道的结构，计算中所需要的参数如表2 所列。为了提高计算精度，将差分格式设置为二阶迎风，收敛精度设为10-6。

表2 计算中所需要的参数

2.1 传统平直并联流道内流体的数值模拟

通过数值模拟，得到的传统平直并联流道内电解液的速度分布图，如图3 所示。

图3 流道内速度分布图

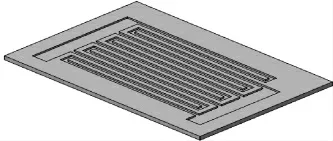
图4 优化后流道结构

由图3 可以看出，离入口较近的支流道内的速度大，支流道离入口越远速度越小。仅凭图中的颜色与左边的标尺就能看出，传统平直并联流道内电解液的分布很不均匀。所以，需要对该流道内流体分布的均匀性进行优化。

2.2 流量分布均匀性的初次优化

由公式（14）可知，增大各支流道的阻力Kc，可以缩小Qj与Qn之间的差距，即可以提高双极板内流量分布的均匀性。增加流道阻力的方法很多，如在流道内设置障碍物等，但设置障碍物将使流道结构变得复杂，增大劳动强度及成本。蛇形流道的缺点是流程长、阻力大，因此在传统平直并联流道的每个支流道上添加一个小型的蛇形流道，以增大各个支流道的阻力。改变后的流道结构即优化后的结构如图4 所示。通过数值模拟，得到的改变结构后流道内电解液的速度分布图，如图5 所示。与图3 相比，改变结构后流道反应区域内各支流道内的速度分布的均匀性，有明显提高。由于各支流道的横截面积相等，所以速度分布均匀即是流量分布均匀。经数值模拟计算，得到改变结构前后全钒液流电池双极板各支流道内的流量，如图6 所示。

图5 改变结构后流道内的速度分布图

图6 改变结构前后流道内流量的分布图

2.3 初次优化支流道流量均匀性判断依据

支流道流量均匀性可以通过两个依据来判断，一是模拟最大误差r，二是理想值的最大误差R[7]。模拟最大误差r= (支管最大模拟流量- 支管最小模拟流量)/支管最小模拟流量；理想值的最大误差R=max（支管模拟流量- 支管理想流量）/支管理想流量。

传统平直并联流道各支流道的理想流量Qideal为：

通过计算，传统平直并联流道的模拟最大误差r为171.55%，跟理想值的最大误差R 为71.99%。初次优化后流道内各支流道的理想流量为：

通过计算，初次优化后流道的模拟最大误差r 为13.82%，跟理想最大误差R 为7.53%。

通过以上的研究分析可知，虽然初次优化后双极板流道内流量的均匀性有很大提高，但是均匀性还不够。因此，还需要对流道进行进一步优化。

2.4 流道的二次优化研究

初次优化后流道内的压力，如图7 所示。由该图可以看出，入口总流道处的压力，离入口越近压力越大；出口总流道处的压力，离出口越近压力越小；而且，入口与出口在同一侧。所以，靠近进出口一侧的支流道的压降较大，离进出口越远的支流道，其压降越小。由于各个支流道的结构、尺寸是完全一样的，因此它们的液压阻力也是一样的，所以压降越小的支流道其流量就越小。由图6 也可以看出，离进出口一侧越远的支流道其流量越小。根据进、出口总流道内的压力分布规律可知，如果将进口与出口放在异侧，那么将会减小各个支流道之间的压降差，进而改善流量的均匀性，二次优化后全钒液流电池双极板流道的物理模型如图8 所示。

通过数值模拟，得到二次优化后流道内电解液的速度分布图，如图9 所示。

图7 初次优化后流道内的压力分布

图8 二次优化后双极板流道的构型

由图9 可以看出，二次优化后反应区域内各支流道的速度分布与初次优化的流道相比，其均匀性又有所改善。下面将经过数值模拟计算，对二次优化前后各支流道内的流量分布进行定量的对比分析，如图10 所示。

图9 二次优化后流道内的速度分布图

图10 二次优化前后流道内流量的分布

由图10 可以看出，全钒液流电池双极板流道进行二次优化后，反应区域内各支流道间的流量均匀性与初次优化相比有明显提高。由二次优化后的流量分布曲线可知，在对双极板流道进行二次优化后，其流量分布已经基本上达到均匀。

2.5 二次优化支流道流量均匀性判断

下面将根据模拟最大误差r 和跟理想值的最大误差R，来判断二次优化后流道内流量的分布是否已经达到足够均匀。

二次优化后流道内流量的模拟最大误差r 为：

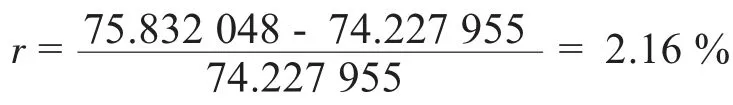
理想值的最大误差R 为：

通过数值模拟与经理论计算得到的模拟最大误差和跟理想值的最大误差的值可知，全钒液流电池双极板流道经过二次优化后，其流量分配已经足够均匀。

3 优化后流道对电池性能的影响

根据文献[8]，一个充放电周期内的全钒液流电池功率图如图11 所示。由图11 可以看出，优化流道的充电电池功率比蛇形流道低，放电电池功率比蛇形流道高。在此种情况下，蛇形流道对应的电池的能量效率为62.55%，优化流道对应的电池的能量效率为66.73%。由图11 以及这两种流道对应的电池的能量效率可知，优化流道的性能高于蛇形流道。再根据文献[9]中的结论，就能得知优化流道的性能也高于另一种常用的传统流道平直并联流道。

图11 一个充放电周期内的全钒液流电池功率

4 结束语

本文主要根据两种常用的传统流道结构平直并联流道与蛇形流道，对全钒液流电池的双极板流道进行了优化。首先，建立了平直并联流道的流体力学模型，根据此模型对流道内流量分布的均匀性进行了优化。然后，在流量分布同样均匀的情况下，将优化流道的流阻与蛇形流道进行对比分析，并对这两种流道对应的电池性能进行了研究。最后，证明了优化流道的性能高于常用的两种传统流道。

在双极板流道的数值模拟过程中，忽略了离子交换膜对流场的影响。为了更精确的模拟流道内的流场，可以建立一个与离子交换膜非常接近的壁面条件，所以在今后的工作中将在这方面作进一步的研究。

[1]徐冬清，范永生，刘 平，王保国.全钒液流电池复合材料双极板研究[J].高校化学工程学报，2011，25(2):308-313.

[2]李国杰，唐志伟，聂宏展，谭 靖，等. 钒液流储能电池建模及其平抑风电波动研究[J].电力系统保护与控制，2010，38(22):115-119.

[3]SKYLLAS-KAZACOS M. An historical overview of the vanadium redox flow battery development at the University of New South Wales,Australia[EB/OL]，2008-11-20.

[4] SUM E, SKYLLAS-KAZACOS M. A study of the V(II)/V(III)redox couple for redox flow cell applications[J]. Journal of Power Sources，1985，（15）:179-190.

[5]SUM E, RYCHCIK M, SKYLLAS-KAZACOS M. Investigation of the V(V)/V(VI)system for use in the positive half-cell of a redox battery[J].Journal of Power Sources,1985,16(2):5-95.

[6]BOERSMA R J, SAMMES N M. Distribution of gas flow in internally manifolded solid oxide fuel-cell stacks [J]. Power Sources,1997,66:41-45.

[7]陈茂斌.钒电池关键材料及外通道流量分配研究[D].重庆：重庆大学材料科学与工程学院,2008.

[8]刘 记. 全钒液流电池双极板流道的优化及流量控制研究[D].长春：吉林大学机械科学与工程学院，2011.

[9]汪 钱，陈金庆，王保国. 导流结构和电极结构对全钒液流电池性能的影响[J].电池，2008，38(06):346-348.