FFT谱连续细化分析在频域模态参数识别中的应用

杨 陈，代洪慧

（中国水利水电科学研究院 工程抗震研究中心，北京 100048）

1 研究背景

经典的传递函数求解方法，一般都是对输入输出数据分段（可以有部分重叠），然后对每段数据分别进行FFT变换，进而得到自功率谱和互功率谱。将分段得到的自功率谱和互功率谱进行平均，利用平均了的互谱与自谱的比值得到传递函数。在计算中，为了充分地利用测试数据、消除混杂在测试信号里的噪声，一般在取段时都要使部分数据重叠（一般取50%），且消除每段的趋势项，加上合适的窗函数[1-2]。

由于谱域的分辨率为：df=fs/nFFT（fs为时域信号的采样频率，nFFT为做FFT变换时的规模），即频域的分辨率取决于时域分段时的长度，为了比较准确地在频域里估计出模态参数，就要求df不能过大，也就要求取段的数据长度nFFT不能太小。在总数据量一定的情况下，这会造成分段数减小，最后得到的频响函数由于平均次数不够，会有很多毛刺，峰值处和模态耦合严重的地方不够光滑。为了获得比较平滑的频响函数曲线，需数据分段较多，每段的数据量减少（nFFT比较小）。这样处理会使频响曲线比较光滑，较大程度地消除了随机误差，使模态定阶问题等容易解决，但却带来一个问题，在频响函数峰值处和模态耦合比较严重的地方，频响函数的数据点数较少，而在频响函数幅值比较小的地方相对较密。本文提出的方法能对频响函数峰值处和模态耦合密集处的传递函数进行加密，使得该区段的数据量增加，而且在该区段同时满足平滑性和高分辨率的特性，从而提高模态参数识别的精度。

2 利用FFT谱连续细化加密传递函数

传递函数反映的是结构在频域的特性：

式中：H(f)为传递函数；F(f)为输入的复数幅值谱；Y(f)为响应的复数幅值谱。

结构在频域里的响应可以用输入与传递函数的相乘来表示，而将实际采样得到的时域信号变换到频域，要利用到快速傅利叶变换FFT。但实际采样得到的信号会混入各种噪声干扰，为了最大程度地排除噪声的影响，采用输入输出的互谱比输入的自谱得到传递函数的一种估计H1(f)，以及用输出的自谱比输入输出的互谱得到传递函数的另一种估计H2(f )等[1]。

传统的频域分析方法是利用离散的傅利叶变换，该方法有分辨率的限制且运算速度较慢。目前国内外的信号处理设备一般都采用快速傅利叶变换（FFT）进行频域分析。传递函数的对应的频率值依赖于FFT变换。为了解决上述计算传递函数时的问题，引入FFT谱连续细化分析算法。

根据文献[4-6]提出的算法，对时间序列x(t)，任意频率f处的离散傅利叶变换（DFT）系数：

其中，fs为x(tk)的采样率；f为指定的频率值（应不超过频谱分析上限0.5fs）。

利用傅氏级数的复指数形式可以写成：

式中：N为x(tk)的数据量；c(f)为傅利叶系数的复数表达。

将上面c(f)的表达式代到H1(f)的表达式里，可以得到加密处的传递函数估计值：

上述3个式子中：N为响应和输入的分段数（分段间一般会有重叠）；fi为指定处的频率值；yk为响应的第k段数据；yk(tj)为响应的第k段数据的第j+1个数据点；fk为输入的第k段数据；fk(tj)为输入的第k段数据的第j+1个数据点；m为分段后，每段的数据点数；Yk为yk的傅利叶变换；Fk为fk的傅利叶变换。

以上以H1(f)估计为例推导了加密算法，H2(f)估计的推导过程类似。在算法实施过程中，由于fi是任意给定的，并不是基频(1 / T)的整数倍，m也不一定是2的整次幂，FFT已经不能使用了。因此在求H(fi)时，只能应用离散傅利叶变换DFT，其计算量为N2，在计算点数比较多时，计算量增加很快。为了加快计算传递函数时，可以只在峰值处和频率耦合比较严重的地方加密。

3 频域模态参数识别方法

频域模态参数识别有单模态识别法，如峰值拾取法、拟合导纳圆法。多模态识别法，如最小二乘法、Klosterman迭代识别法、Levy法和正交多项式拟合法[1]等。本文采用的Levy法对模态耦合比较严重的情况有良好的识别精度，其计算原理是：在给定的传递函数离散数据点H(w)处，拟合有理多项式,确定多项式的系数，最后由分母多项式的系数求得模态频率和阻尼比，分式的极点值得出留数，最后由不同测点的留数值估计出振型[1-3]。传递函数的表达式为：

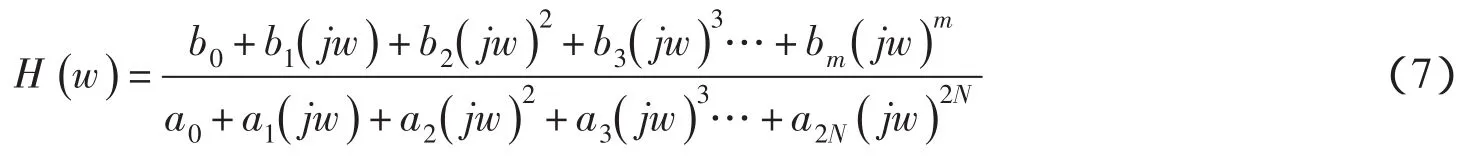
式中：N为模态阶次；当传递函数为加速度传递函数时，m为2N；当传递函数为速度传递函数时，m为2N-1；当传递函数为位移传递函数时，m为2N-2。由归一化可以令a2N为1。

很明显，式（7）为非线性拟合。经典的Levy法中误差向量写为：

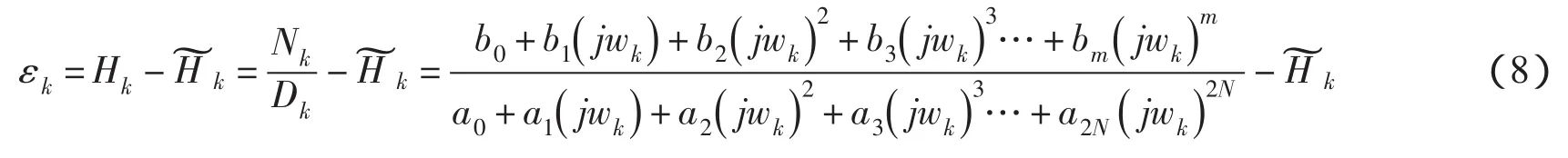
式中：Dk=a0+a1(jwk)+a2(jwk)2+a3(jwk)3…+a2N(jwk)2N；Nk=b0+b1(j wk)+b2(jwk)2+b3(jwk)3…+bm(jwk)m；Hk为理论值；为实测的传递函数值。

化非线性为线性误差为：

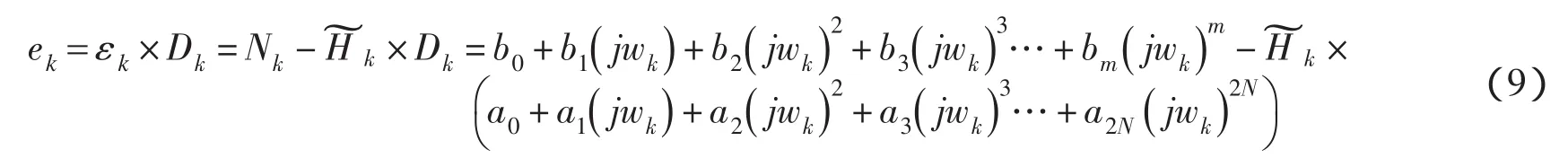
则误差的平方和是：

式中：C为常数；{θ}为未知系数{a}{b}构成的列向量：

根据E最小的要求，应使

由此可以得到：

最后由式（13）求出系数{a}、{b}，由分母的复根求出频率和阻尼比，由传递函数在极点处的值得到留数，最终求得模态参数。

4 FFT谱连续细化和Levy法联合运用

联合运用谱连续细化算法和Levy法进行模态识别，主要步骤如下：（1）将实测的输入输出数据用经典的传递函数算法给出估计。这一步中，可以使分段数比较大，频域分辨率比较低，但可以得到比较光滑的传递函数曲线。从而容易地分辨出模态阶次和固有频率的大致范围，以及模态耦合比较严重的区段；（2）选取需要加密的主模态区间以及模态耦合严重的区段。在区段里，设定出需要达到的加密后的频率分辨率，以及加密的点数。在每个加密点对应的频率值处，根据式（4）所给出的内插算法，计算出该点的传递函数值。则加密后的传递函数值与之前给出的～H 1构成了最终的传递函数估计值～H ；（3）用Levy法算出实测频响曲线～H 所对应的数学模型式（8）的系数值：X0=[b0，b1，b2，…bm；a0，a1，a2，…a2N]；（4）根据经典的Levy法算出模态参数；（5）如果要求更精确地求出模态参数，可以在步骤（2）中调整加密区段和加密后的分辨率，然后运用Levy法求出模态参数，考察模态参数的稳定性，确定比较稳定可靠的模态参数。

从上述算法过程可知加密后的传递函数，其主模态区间以及模态耦合严重的区段数据量大大增加，而且在该区段同时满足了平滑性和高分辨率的特性。由于运用Levy法求解模态时，着重强调了主模态区间以及模态耦合严重区段的拟合误差中，因此模态识别精度得以提高。而传统Levy法的拟合误差仅仅强调了未加密前的传递函数实测值处的误差，这是与本文算法的最大的不同点。

5 算例

本文给出两个算例，一个数值仿真和一个实测算例来验证本算法的有效性。

5.1 算例1选取一个四自由度的弹簧质点模型（见图1），用白噪声激励，根据加速度响应进行算法验证。在质量单元2处施加160s的白噪声激励，并在第一质量单元m1的加速度响应中混有噪声干扰。利用质量单元1的加速度响应求传递函数H12(f)。激振力的采样频率和响应的采样频率均为250Hz。

采用H1估计传递函数，分段长度为2 048点，频率分辨率为：df=250/2048=0.1221Hz，每段重叠了1 024点，每段里施加“hanning”窗。得到输入点2和响应点1间的传递函数H12(f)，如图2所示。将传递函数H12(f)的6.5～32Hz间的部分的加密，共加密了1 275个点，加密后的传递函数的分辨率接近0.02Hz，如图3所示。

应用Levy法拟合加密前、后的传递函数H12(f)，如图4、图5所示。实线是根据输入、输出响应计算得到的传递函数H12(f)，点划线是Levy法拟合H12(f)的值。采用Levy法拟合传递函数H12的结果如表1所示。

由图4、图5及表1可以看出，FFT谱连续细化分析和Levy法联合运用的优势，其4阶模态都能够比较准确地识别出来，未加密的算法的误差比较大。上述的加密算法不仅能用在传递函的计算方面，还可以用在自功率谱、互功率谱估计等方面，能够给出更加平滑、饱满的曲线（峰值处半功率带宽里可以达到8个点以上）。

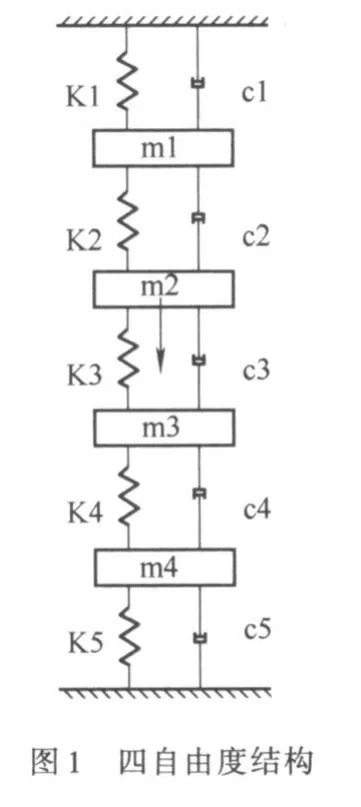
图2 传递函数H12（f）幅频

图3 加密了的传递函数H12（f）幅频（圆点为内插值）

图4 Levy法拟合未加密的传递函数H12幅频

图5 Levy法拟合加密的传递函数H12幅频

表1 Levy法拟合传递函数H12的结果

5.2 算例2下面给出了本文的算法在某大型升船机振动台模型试验研究[7]中的应用。该升船机承重塔柱长119m，宽57.8m，高145m，由对称布置4个塔柱构成。模型的长度比尺为1∶25，在塔柱模型上布置了51个加速度传感器，模型底板上表面分别沿X、Y、Z方向各布置1个，模型塔柱四角沿竖向隔层布置1～2个。

在第一阶段小震情工况时，沿横河向输入了50gal的白噪声激励，得到了试验前模型的动力特性。选取台面顺河向的输入时程和塔柱上横河向第23#测点的响应验证本文的算法。

采用H1估计传递函数，并将传递函数H(f)的1～60Hz间的部分加密，共加密了3 000个点。加密前的频率分辨率为0.25Hz，加密后为0.019 7Hz。如图6、图7所示。

应用Levy法拟合加密前、后的传递函数H(f)，得到前3阶模态参数，如图8、图9和表2所示。

由表2可以很明显地看出本文提出的细化算法的优势。由图8、图9可以看出，加密后的传递函数的拟合值与实测传递函数值相当吻合，而且拟合的传递函数曲线比较平滑，阻尼比的识别精度有很大的提高，且第四阶模态参数的识别结果也优于未加密前的结果。本文的算法在实际应用中得到了验证。

图6 未加密的传递函数幅频

图7 加密后的传递函数幅频（圆点内插点）

图8 Levy法拟合未加密的传递函数幅频

图9 Levy法拟合加密后的传递函数幅频

表2 某大型升船机塔柱模型横河向前3阶模态参数

6 结语

本文提出了一种利用FFT谱连续细化算法对传递函数在峰值处和模态耦合密集处进行加密，然后利用Levy法进行模态参数识别的算法。数值仿真结果表明，此算法在区分密集模态和提高模态参数识别结果方面有较大的改进，而且在抗噪声方面有很大的优势。但改进算法在加密传递函数时，由于不能采用快速FFT变换，导致计算量比较大，为了加快计算传递函数，可以选择在峰值处和模态耦合比较严重的地方加密。应用本文算法在某大型升船机振动台模型试验中取得了良好的结果，验证了其实际应用价值。数值实验和实测实验都很好地验证了本文算法的有效性。

[1]李德葆，陆秋海.实验模态分析及其应用[M].北京：科学出版社，2001.

[2]王济，胡晓.MATLAB在振动信号处理中的应用[M].北京：中国水利水电出版社，2005.

[3]傅志方.振动模态分析与参数辩识用[M].北京：机械工业出版社，1990.

[4]刘进明，应怀樵.FFT谱连续细化分析的富里叶变换法[J].振动工程学报，1995，8（2）：162-166.

[5]孙鹤泉.实用Fourier变换及C++实现[M].北京：科学出版社，2009.

[6]Stefan Hollos，Richard Hollos.C Program Magnifies Spectrum When An FFT Can’t Hack It Highlights[OL].http：//electronicdesign.com/article/embedded/c-program-magnifies-spectrum-when-an-fft-can-t-hac.aspx.August 18，2003.

[7]中国水利水电科学研究院.某升船机塔柱大型振动台抗震试验研究报告[R].北京：中国水利水电科学研究院，2009.