电励磁风力发电系统机侧控制策略研究

霍现旭， 胡书举， 许洪华

(1.中国科学院电工研究所，北京 100190;2.中国科学院研究生院，北京 100049)

0 引言

电励磁同步电机具有功率因数高且可调、过载能力强、转动惯量小等优点，在水电、火电中得到了广泛应用。德国Enercon等公司已经将电励磁同步发电机应用于风电系统中，国内湘电等一些公司也在进行电励磁风力发电系统的研制。目前国内的主流机型为使用双馈感应发电机(Double-Fed Induction Generator，DFIG)的双馈型风电系统和使用永磁同步发电机(Permanent Magnet Syndronous Generator，PMSG)的直驱型风电系统［1］。相比于DFIG，电励磁同步发电机具有功率因数高、弱磁区转矩特性好等优点;相比于PMSG，电励磁同步发电机具有无需永磁材料、无失磁风险、可调励磁磁通、造价相对便宜等优点，显示了一定的优越性能。

同步电机的矢量控制系统可分为转子磁场定向控制、定子磁场定向控制、气隙磁场定向控制等方式［2］。转子磁场定向控制系统结构简单，定向容易，只需检测转子轴线位置即可实现定向，一般用于永磁同步电机控制中。文献［3］等采用了定子磁链定向控制，文献［4-5］等采用气隙磁链定向控制。在不同的控制目标和控制方式下，定子磁场定向控制和气隙磁链定向控制对于转子激磁电流、功率因数、系统稳定性等方面影响不同，各有优劣。本文采取气隙磁链定向矢量控制系统。

气隙磁场定向控制能够得以有效实现的关键，在于电机磁链信息的准确获取。对电励磁同步电机磁链观测常用的方法有电流模型、电压模型和混合模型。电流模型在低转速时能够快速跟随给定，缺点是对电机参数敏感，电机参数受外界影响变化时，模型不能很好的工作。传统的电压模型是对反电动势直接积分，为开环模型，积分累积误差和直流偏移误差较大。为了消除这些误差，部分文献采用了低通滤波器代替积分环［6］、饱和双反馈积分器［7］、MT轴系感应电势辨识［8］等策略加以改进。

本文以电励磁同步发电机为研究对象，针对其在风力发电系统中的应用，对气隙磁场定向矢量控制进行了研究，对气隙磁场定向中的磁链观测和控制方案进行详细阐述，并给出了仿真结果。

1 气隙磁场定向下的同步发电机数学模型

为了实现电机转矩和磁场的解耦控制，通过坐标变换将同步发电机的abc坐标系等效变换到同步旋转MT轴坐标系中，其中，同步旋转轴线M轴与气隙磁链矢量ψδ重合。将定子电流is沿MT轴分解为激磁分量ism和转矩分量ist，分别控制便可实现解耦，简化同步电机的控制。不同轴系的相对位置关系及矢量关系图如图1所示。

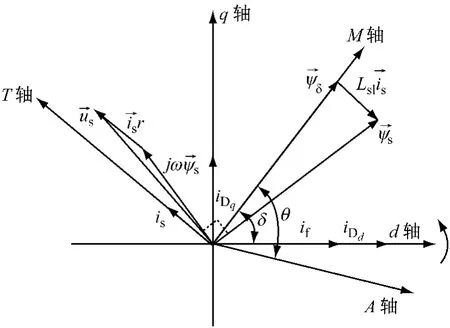
图1 电励磁同步电机矢量图

在气隙磁链定向控制中，采用电动机惯例，坐标变换采用恒幅值变化，可得到气隙磁链表达式如下:

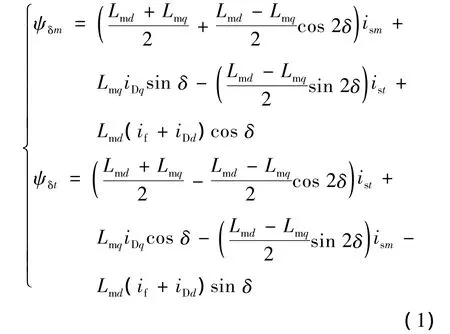
式中:ψδm、ψδt——M、T轴磁链分量;

Lmd、Lmq——d、q坐标系下的d、q轴互感;

ist、ism——M、T轴定子电流分量;

if——励磁电流;

iDd、iDq——d、q轴阻尼电流分量;

δ——功角，即转子与气隙磁链之间的夹角。

根据气隙磁链定向原理可知 ψδt=0。从式(1)可看到，阻尼绕组只在动态时对气隙磁链产生影响，且凸极效应对磁链幅值的影响很弱，定子电流磁场分量ism和转子激磁电流if是气隙磁链的主要作用量。因此，在稳态时，可以忽略凸极效应影响和阻尼绕组的影响，气隙磁链的表达式简化为

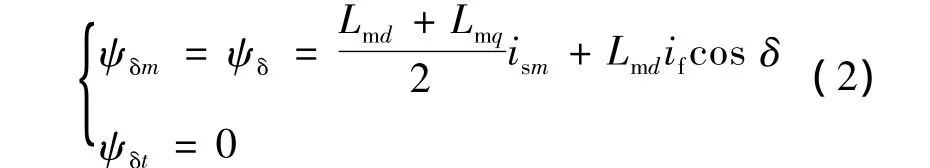
MT轴系下电励磁同步电机的电压方程为

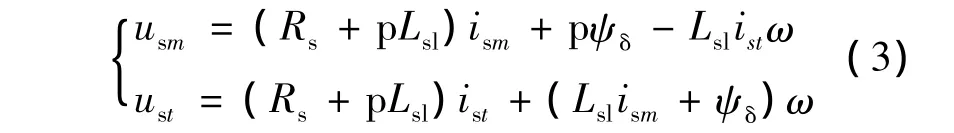
其中:ust、usm——M、T轴定子端电压分量;

Rs、Lsl——定子绕组电阻和漏电感;

ω——同步坐标系旋转角速度。

转矩方程为

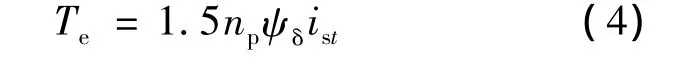
2 同步发电机气隙磁链观测

传统的电压模型面临着积分零点漂移的问题。文献［3］提出了一种采用MT轴系感应电势辨识磁链的方法，有效解决了传统电压模型中存在的问题。这种方案的控制框图如图2所示。

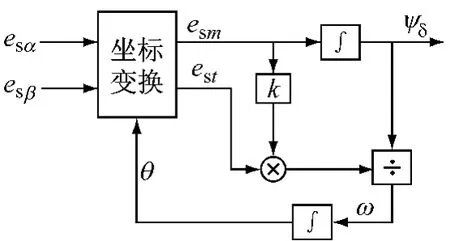
图2 基于MT轴系的气隙磁链观测

在MT轴系坐标系下，假设气隙磁链产生的感应电势与T轴不重合，定子感应电势矢量在MT轴上分解为转矩分量est和磁场分量esm，则感应电势方程为

根据式(5)，可以得到:

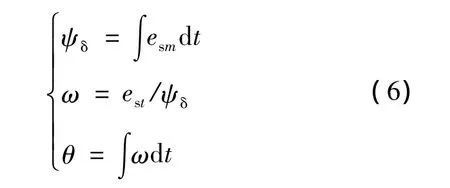
基于MT轴系感应电势观测气隙磁链的积分器处于闭环中，漂移能够被抑制，可以直接输出气隙磁链的幅值和相位，也为电励磁同步电机无速度传感器控制提供了转速和角度值。

3 矢量控制策略

风力发电系统中，变流器接收的主控命令为转矩命令，依据式(4)可得到转矩参考电流。根据所设定的发电机功率因数，输入气隙磁链幅值和发电机的转矩参考电流，可得到定子励磁参考电流。本文中，设定电机内功率因数为1，即定子电流与气隙磁链垂直。根据式(3)，定子的MT轴系电流经过PI调节器，再加上前馈补偿项，就可以得到MT轴的参考电压矢量ust和usm。再经过坐标变换得到三相参考电压usa、usb和usc，最后进过SVPWM算法得到发电机的控制信号。

在电励磁同步电机的气隙磁链矢量控制中，须保持气隙磁链幅值的恒定，即保持激磁电流iμ恒定。根据式(2)，稳态时气隙磁链主要与定子M轴电流ism和转子激磁电流if有关，动态时还与阻尼绕组电流iD有关。由于控制中定子电流与气隙磁链垂直，故有ism=0。稳态时，阻尼绕组电流为0，由式(2)可看到此时气隙磁链仅与励磁电流和功角有关。气隙磁链参考值与磁链观测器所得到的气隙磁链幅值的差值送入PI调节器，得到所需要的激磁电流参考值。由于定子M轴电流ism已确定，转子激磁电流参考值也可以唯一确定。

根据上述原理可得到机侧变流器的整体控制框图，如图3所示。

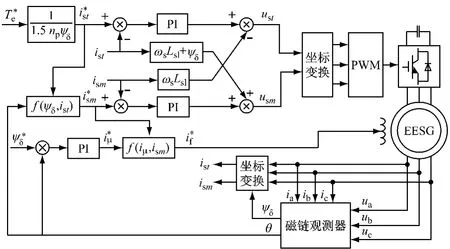
图3 电机侧变流器控制原理图

4 仿真验证

基于上述工作原理，在MATLAB/Simulink 7.11中搭建了电励磁同步发电机与电机侧变流器的仿真系统。为模拟风速变化对电流跟随能力的影响，转速给定由初始的100 rad/s在0.3 s时斜坡给定至150 rad/s。为了验证实际工况中主控给定的转矩变化对电流变化的影响，转矩给定由初始值时的 －135 N·m在 0.6 s时变为－225 N·m。磁链参考幅值设定为1.5 Wb。仿真中电机的参数如下:额定功率31.3 kW、定子电阻0.214 Ω、定 子 漏 感 1.025 mH、直 轴 电 感24.36 mH、交轴电感 11.67 mH、极对数2。

图4为磁链观测器模型得到的磁链幅值和相位的变化曲线。由图可看出，初始经过短暂的暂态后，相位和幅值很快收敛至稳定;在速度发生变化后，磁链观测模型能很快进行跟踪，并且转矩突变对其影响不大，显示了磁链观测器良好的动态性能和鲁棒性。该磁链观测器在系统的整个运行范围内能够保持幅值恒定，消除了由于直流偏置和积分累积导致的误差。

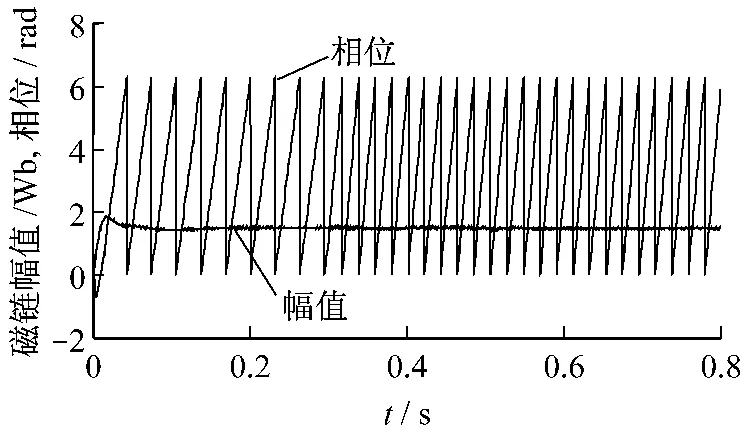
图4 磁链幅值和相位观测值

图5和图6分别为电机转速和转矩的变化曲线，图6给出了参考转矩和实际转矩的对比曲线。图7是定子转矩电流ist和激磁电流ism在转速和转矩突变情况下的变化曲线，图8为相应的定子三相电流波形。由图5可看出，在参考转矩突变时，系统的实际电磁转矩能够很好地进行跟踪，并且脉动很小。从图6中可看出在0.3 s转速发生变化时，定子转矩电流和激磁电流脉动很小;在转矩发生突变时，定子的转矩电流ist也发生突变，验证了在磁链幅值不变的情况下，电磁转矩与转矩电流成正比的关系;整个过程中，定子的激磁电流ism基本为0，即定子电流与气隙磁链基本保持垂直，维持内功率因数为1不变。

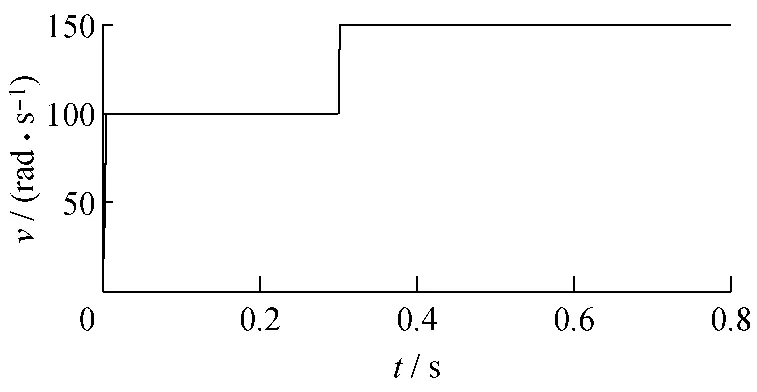
图5 电机转速曲线

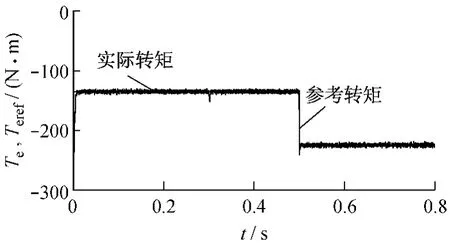
图6 参考电磁转矩和实际电磁转矩曲线

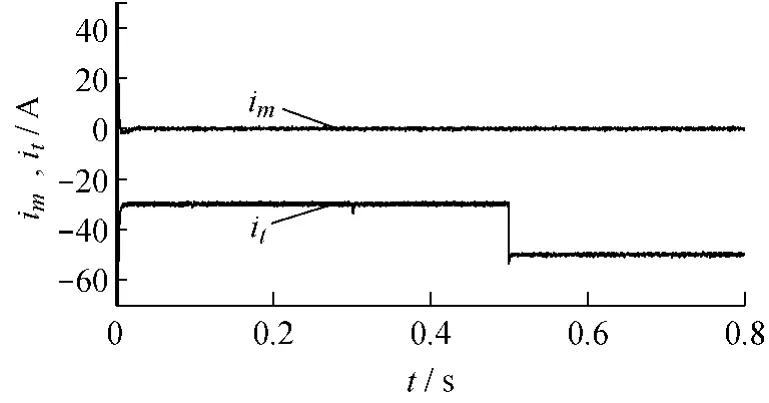
图7 MT轴电流波形

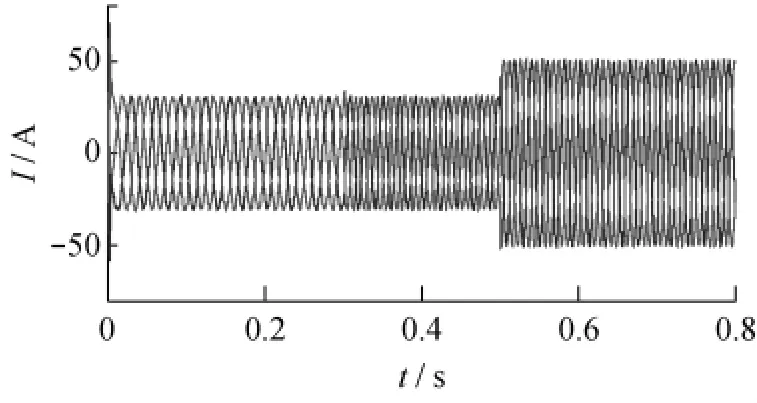
图8 定子三相电流

5 结语

本文针对电励磁同步发电机在风力发电中的应用，提出了机侧的控制策略，并对控制中的磁链观测和控制策略进行了详细分析，通过仿真验证了控制策略的有效性。由仿真可知，在风速和转矩突变时，磁链观测器能准确观测气隙磁链的幅值和相位，发电机能够稳定运行，控制效果良好。

［1］牟迈.风力发电机市场品牌集中度趋高，质量稳定性仍待提升［J］.风能，2011(5):42-44.

［2］李崇坚.交流同步电机调速系统［M］.北京:科学出版社，2006.

［3］HOFMANN H F，SANDERS S R，EL-ANTABLY A.Stator-flux-oriented vector control of synchronous reluctance Machines with maximized efficiency ［J］.IEEE Transactions on Industrial Electronics，2004，51(5):1066-1072.

［4］PENG L Q，XIE L，WU F，et al.Field-oriented control of synchronous motor based on adaptive extended Kalman filter［C］∥IEEE International Conference on Cloud Computing and Intelligence Systems(CCIS)，2011:633-637.

［5］吴轩钦，谭国俊，宋金梅，等.基于混合磁链观测器电励磁同步电机矢量控制［J］.电机与控制学报，2010(3):62-67.

［6］HU J，WU B.New integration algorithms for estimating motor flux over a wide speed range［J］.Power E-lectronics，IEEE Transactions，1998，13(5):969-977.

［7］刘军锋.基于U-I模型的感应电动机定子磁链观察模型方法研究［J］.电气传动，2008，38(4):20-24.

［8］WEI X S，MA X L.Some techniques of vector control systems of medium voltage three-level inverters［C］∥Power Electronics and Motion Control Conference，IPEMC04，2004(3):1399-1403.

［9］SHINNAKA S，SAGAWA T.New optimal current control methods for energy efficient and wide speed range operation of hybrid field synchronous motor［J］.IEEE Trans on Digital Object Identifier，2007，54(5):2443-2450.

［10］周二磊，符晓，王珂，等.基于混合磁链模型的电励磁同步电动机矢量控制研究［J］.变频器世界，2011(1):56-58.