一种双馈电机转子电流定向的矢量控制方法*

陈显彪

(南昌工程学院机械与电气工程学院，江西南昌 330099)

0 引言

双馈电机具有良好的调速性能、效率高、可改善功率因数和提高电网的稳定性等特点，特别适合于风机、水泵、压缩机等机械的调速传动[1]在双馈调速系统的设计和研究中，为了使系统的动、静态性能达到最佳，通常采用矢量控制的方法。其核心思想是将交流电机的电流矢量分解为相互独立的产生磁场的励磁电流分量和产生转矩的转矩电流分量，将磁链与转矩解耦，再根据磁场定向原理分别设计两者的调节器，分别控制两个分量的幅值和相位，从而实现对电机的高性能调速。

1 双馈电机转子电流定向矢量控制

1.1 双馈电机在两相同步旋转坐标系上的数学模型

在同步旋转的d、q坐标系上，双馈电机的数学模型可用下列4个矩阵方程表示[2]。

磁链方程:

电压方程:

转矩方程:

运动方程:

式中:Rs、Rr——分别为定、转子绕组电阻;

Ls、Lr、Lm——定、转子绕组自感及定、转子绕组间的互感;

ω1——同步旋转角速度;

ω——转子旋转角速度;

ωs——转差角速度，ωs= ω1－ ω;

np——电机极对数;

TL——负载转矩;

J——机组转动惯量;

p——微分算子，p=d/dt。

根据双馈电机的磁链方程式(1)的前两行求出isd和isq:

将式(5)、式(6)代入转矩方程式(3)，可推得双馈电机转矩方程的另一种形式:

1.2 双馈电机的转子电流定向矢量控制原理

根据电机的基本理论，在忽略定子绕组电阻的情况下，双馈电机定子磁链矢量ψs在定子绕组中感应的电动势矢量es与定子所接电源电压矢量us平衡，即有us=－es。如果电机的定子绕组接到电压稳定的三相对称工频电源上，电压矢量us不变，则定子绕组感应电势矢量es，以及在定子绕组中感应出es的定子磁链矢量ψs均保持不变。

由上可知，如果将同步旋转的d、q坐标系的d轴放在定子磁链ψs的方向上，改称作M轴，q轴改称作T轴，则ψsd改写为ψsm，其值即为定子磁链矢量ψs，而ψsq改写为ψst，其值为零，此所谓定子磁场定向。其矢量图如图1所示。

由图1还可见，由于es滞后ψs90°，us超前ψs90°，且只有T轴分量ust，M轴分量usm为零。

进行定子磁场定向后，转矩方程式(7)改写为

图1 双馈电机定子磁场定向矢量图

由于ψsm=ψs，ψst为零，方程可进一步简化为

如前所述，电机定子绕组接到电压稳定的三相对称工频电源上时，定子磁链矢量ψs保持不变。因此，根据式(9)，只要改变irt的大小，即可改变电机的电磁转矩Te，从而实现电机的高性能矢量控制调速。

转子电流的M轴分量irm的存在，会降低系统的功率因数，并影响系统的稳定，应采取措施进行抑制。提出的一种解决方法是在转子施加与转子电流矢量ir反相的外加电压ur，但该方法在亚同步工况时可行，在超同步工况时则系统会失去稳定[3]，其原因在于超同步工况时系统不能对irm进行有效抑制。为解决这一问题，可以对转子电压矢量ur的M轴分量urm和T轴分量urt分别进行控制。其中，通过对urm的控制来抑制irm，以维持irm基本为零，而通过对urt的控制来改变irt，以改变电机的电磁转矩，实现对电机的调速。由于irm=0，转子电流矢量ir=irt，其方向始终为T轴方向，因此称这种控制方法为转子电流定向的矢量控制方法。

2 双馈电机的转子电流定向矢量控制仿真试验

2.1 仿真试验模型的建立

为了验证前述双馈电机调速控制方法的正确性，根据前述双馈电机在两相同步旋转坐标系上的数学模型，应用MATLAB的S－函数建立了双馈电机仿真模块“DoublyfedMachine”，并在 MAT LAB∕Simulink环境中，以该电机仿真模块为控制对象进行了仿真试验。电机的参数如下:额定功率PN=2.2 kW;额定转速nN=1 440 r/min;极对数np=2;定子额定电压UsN=380 V，星形接法;定子额定电流IsN=5 A;定子额定频率f1=50 Hz;转子额定电压UrN=300 V;转子额定电流IrN=6 A;定子电阻Rs=3.25 Ω;转子电阻Rr=2.96 Ω;定子电感Ls=0.279 H;转子电感Lr=0.279 H;定转子互感Lm=0.265 H;机组转动惯量J=0.047 kg·m2。双馈电机仿真模块“DoublyfedMachine”的定子绕组接380 V三相对称电源，频率 f1=50 Hz，角频率为 ω1=2πf1，定子各相电压为

将其变换到两相同步旋转坐标系，得

由上，取定子电压M轴分量usm=0 V、定子电压T轴分量ust=－380 V。

为保持转子电流M轴分量irm=0，设计了irm的调节通道。给定值=0，将irm作为反馈量(负反馈)，当irm＞0时，电流调节器ACR的输入为负，输出urm减小，使irm减小，反之使irm增大，从而达到保持irm=0的目的。电流调节器ACR采用PI调节器以保证快速响应及较小的超调量，并消除静差。通过分析和试验，其传递函数取为

转子电压T轴分量urt的取值由Simulink的4个斜坡函数发生器Ramp1～Ramp4产生，其波形如图2所示。

图2 转子电压T轴分量urt

负载转矩TL取电机的额定转矩14.6 N·m，为一恒转矩负载。

2.2 仿真试验及结果分析

在MATLAB中运行图2所示的仿真模型，进行双馈电机转子电流定向矢量控制仿真试验，得到转子电流M轴分量irm的输出波形，如图3所示。

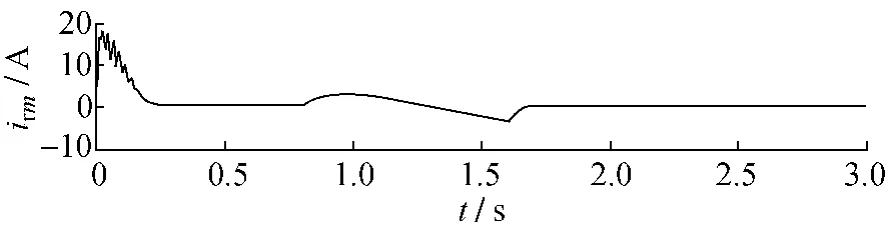
图3 转子电流M轴分量irm

由图3可见，电机刚接上电源时，irm较大，但在irm的调节通道的作用下，其值很快降为零，并在urt变化时，其值波动也不大，说明irm调节通道对irm的抑制效果良好。

图4为在电机施加图2所示的urt的情况下，电机的转速波形。

图4 电机转速

比较图2和图4可看出，通过改变urt，可实时控制电机的转速n，且系统的动态响应较快，转速n的变化相对于urt的变化滞后很小。并且不仅在转速低于同步转速(1 500 r/min)的亚同步转速运行时能实现调速，在转速高于同步转速的超同步工况时同样能实现调速，性能稳定。

3 结语

本文在阐明双馈电机的转子电流定向矢量控制原理的基础上，应用MATLAB/Simulink构建了双馈电机转子电流定向矢量控制仿真试验模型。仿真试验的结果证明了所提出的矢量控制方法不仅在亚同步工况下可行，在超同步工况时同样可行，系统的调速性能良好。

[1]黄守道.双馈电机的工业应用展望[J].湖南大学学报(自然科学版)，1999，26(4):67-70.

[2]陈伯时.电力拖动自动控制系统:运动控制系统[M].北京:机械工业出版社，2003.

[3]陈健.一种新型的双馈电机的矢量控制方法[J].微计算机信息，2007，23(7-1):24-25.