别再拿宝贵的经验固化鲜活的学生——2011年高考数学安徽卷理科第19题赏析及教学启示
☉安徽省亳州市第一中学 史 嘉
一、背景介绍
2011年是安徽省高考数学自主命题的第六年,也是新课标高考的第三年,就是这过渡期后期的数学卷,遭到公众的口诛笔伐,“难”声不绝于耳.真的难吗?难在哪儿?因何而难?笔者及时搜集师生的反馈信息,分析发现,难点恰是亮点,亮点就是变化.其中最出乎意料的是解答题第19题——不等式证明.
二、试题赏析

(2)设1 安徽卷与江苏、广东等省市的试卷相比,比较“稳重”,甚至是保守的,而该题是个例外.两不等式构思新颖,散发出不俗的简洁美和轮换的对称美,涉及不等式的基本性质,对数函数和换底公式等知识,考查代数式的恒等变形能力和推理论证能力.先看标准答案: 其中x=logab≥1,y=logbc≥1. 故由(1)立知所要证明的不等式成立. 难题,常以“技巧新颖、思维别致、运算烦琐”为主要特征,往往都是形式出乎学生的意料而造成的心理不适和消极暗示.该题满分12分,平均得分仅1.8,从0.15的难度系数看,应该是名副其实的超难题目了.纵观五年的安徽卷,包括近几年各省市的数学考卷,单纯拿不等式命制解答题的寥寥无几,即使考查也仅是“搭便车”式的,比如依附导数题,“傍”数列题,等.严格地说,该题打了个“擦边球”,因为在2011年的《考试说明》里,必修5模块“不等式”中没有不等式证明的要求,在“不等式选讲”模块的要求也仅是:“通过一些简单问题了解证明不等式的基本方法:比较法、综合法、分析法、反证法、放缩法”,且只是“了解”层次.该题还有拼凑之嫌,若只设置一个不等式证明显然份量不够,于是弄了两小题,其实两者隐含的“借步作答”关系在紧张的考场里很难被察觉.下面给出有别于文[1]的一种基本证法. 证明:(1)作差后分组,再因式分解得: (2)由1 接下来,先等价变形不等式(2),再拓展.令x=ln a,y=ln b,z=ln c,由1 对数不等式可推广为,若1 2012年的备考进入冲刺期,从这道题我们获得什么教学启示呢?最近和安徽《中学数学教学》编辑张老师聊天,他一语中的:“由今年高考可以看出,考生的数学素养差,教师复习时太看重上一年的题型、模式啦!” 一方面,考生的运算能力和代数变换能力较薄弱,这应归因为新课改等诸多因素.初中对代数变换能力要求降低,学生缺乏对代数变换重要性的认识,忽视对计算变形方法和准确性的训练,而高中教师对代数变换能力的训练也缺乏足够大重视.所以,高中教师要高度重视对学生代数变换能力的培养,注重在平时的教学中进行渗透.不仅要重视解题思路的分析,而且更应该注重学生解题过程的运算.对于烦琐的公式和方程的推导,也要让学生体验这个过程.只有让他真正“锄禾日当午”了,才能深刻体会“粒粒皆辛苦”的内涵.比如,点到直线的距离公式,椭圆的标准方程,甚至线性回归方程等,不失时机地给学生创造手脑并用的机会,使得学生在思想上和行动上都更加重视运算能力和代数变换能力的训练. 另一方面,我们一线教师过分关注以往试卷的题型和模式.往深了说,又是应试教育惹的祸.我们知道,知识本没有“热点”和“冷点”之分,所谓“热点”或者“重点”其实就是经验的积累和记忆的叠加,而学生是活的,考卷是变的.因此,不能过分看重往年的题型和模式.有人说经验大于学问,但经验往往也会无意中让人思维定势和僵化.其实,自信心和应变能力以及锲而不舍的钻研精神比知识更重要,这正是新课改所倡导的.然而,课程标准已实施多年,但一些教师的教学思想还是无法转变,尤其在数学学科上,仍以模拟训练为主.该道及安徽卷给我们传递一个强烈的信息:单纯地依靠试题训练行不通,“题海战术”和“题型教学”可以休矣! 别再拿咱们宝贵的经验固化学生的鲜活思维!我们培养的不是流水线边动作敏捷思维程序化的工人,更不是流水线上统一规格的产品,而是有血有肉、有思想、有激情、有创造力的人才. 1.陆学政.脚下本有多条路,缘何无法通“罗马”——从一道高考题谈高中生代数变换能力的培养[J].中学数学,2011,8.

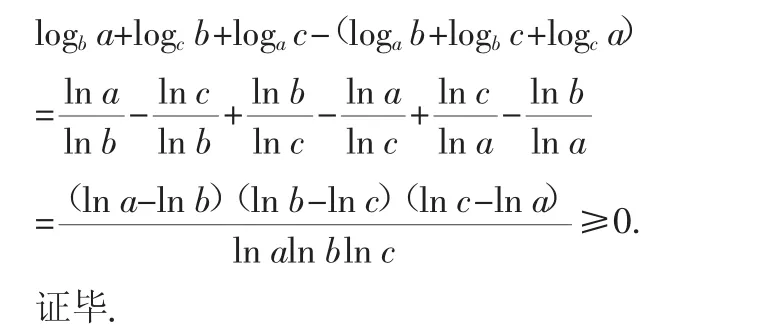
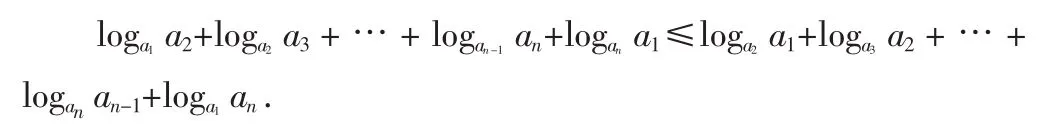
三、教学启示

