填空题的赏析与思考一道2012年江苏高考

☉江苏省宝应县氾水高级中学 盛兆兵

填空题的赏析与思考一道2012年江苏高考

☉江苏省宝应县氾水高级中学 盛兆兵

今年江苏考生考完数学后，都说填空题第14题比较难，为什么学生都说这题难呢？主要原因在于本题变量较多，而且关系复杂，学生理不清头绪，不敢往下计算.若学生掌握主元法，则很快算出答案.

在许多数学问题中，都含有常量、参量、变量等多个量（统称为元素）.这些元素中，通常情况下，有一些元素处于突出和主导的地位，可视为主元.在有些情况下，为解决问题的需要，也可人为突出某个元素的地位作用，将之作为主元.这种确定主元后，以此作为解题的主线，进而把握问题，促使问题转化，直至问题解决的思想方法称为主元法.

例 （2012年江苏14）已知正数a，b，c满足：5c－3a≤b≤4c－a，clnb≥a+clnc，求的取值范围.

分析：本题中出现三个变量，而且满足的关系式比较复杂，选择哪一个或哪两个作为主元，是求解本题的关键.的

几何意义是（0，0），（a，b）这两点的斜率，所以本题把a，b作为主元，c看作常量.

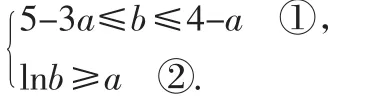
变式1：（2011年苏州高三第一学期期末第13题）已知△ABC的三边长a，b，c满足b+2c≤3a，c+2a≤3b，求的取值范围.

分析：本题中出现三个变量，而且在三角形中，处理方法与上例类似，把a，b作为主元，通过三角形的三边关系消去c.

解：因为b+2c≤3a，所以2c≤3a－b.

由于a，b，c为三角形的三边，

说明：本题也可采用线性规划方法求解，共有7个不等式，有5条直线，正确地找出可行性区域，对学生要求较高，难度大.若采用主元法，能简化计算，且能节约时间.

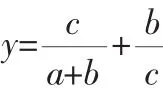
分析：不少学生面对此题，感觉无从下手.本题求解的关键是根据主元思想，减少变量.

解：由题意分析把b，c作为主元，且满足b+c≥a.

以上对主元法做了初步研究，其中蕴含辩证思想.一方面，当我们遇到含多元问题时，面对诸多元素，主元策略往往给我们一个头绪，一条主线，体现了化归转化思想；另一方面，主元法还表现于主元选择的变通性，选择不同主元，形成不同解题途径，最终又殊途同归，体现了和谐统一、普遍联系的观点.