初显端倪的“几何概型”中考题超纲吗？

☉北京师范大学出版集团 岳昌庆

☉江西省新余市渝水区罗坊中学 胡 俊

初显端倪的“几何概型”中考题超纲吗？

☉北京师范大学出版集团 岳昌庆

☉江西省新余市渝水区罗坊中学 胡 俊

近年的全国各地中考试题中，概率部分好题连连，请看2011年呼和浩特市卷第14题（3分）.

例1 在半径为2的圆中有一个内接正方形，现随机地往圆内投一粒米，落在正方形内的概率为__________.（注：π取3）

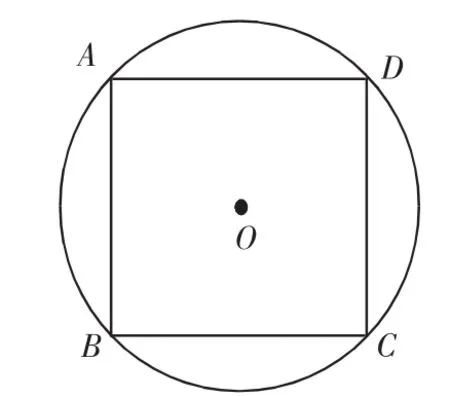
图1

评注：严格地说，这是一道几何概型问题，而课程标准中对概率考核的要求是“能计算简单事件发生的概率.在教学中，应注重所学内容与日常生活、自然、社会和科学技术领域的联系，使学生在具体情境中体会概率的意义”［1］［2］．

这道中考题似乎是超纲了，但实际上不然.课程标准中又有“对有关术语不要求进行严格表述”［1］，且课程标准中还有以下“案例”供编写教材及教学时参考.

例2 如图2，转动转盘，求转盘停止转动时指针指向阴影部分的概率.［1］

这就不难理解为何例1不算超纲了.随机思想是统计与概率的灵魂，新课程提倡数学来源于生活，在具体情境中了解概率的意义，通过实例进一步丰富对概率的认识，并能解决一些实际问题.让学生在数学教学实践中体会这种思想是十分必要的.中考概率问题不只单纯考查概率知识，还要考查其他数学知识，如方程、函数、几何图形等.

例3（2011年高考福建卷理科第4题、文科第7题5分）如图

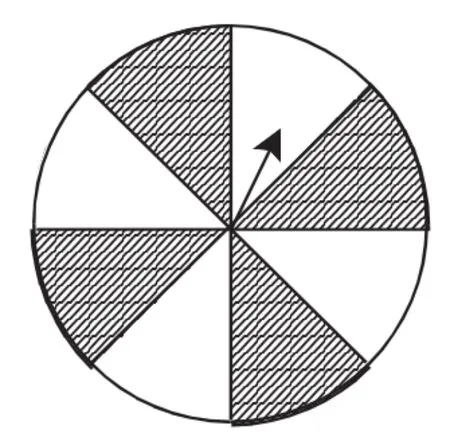
图2

3，矩形ABCD中，点E为边AD的中点，若在矩形ABCD内部随机取一个点Q，则点Q取自△CBE内部的概率等于（ ）.

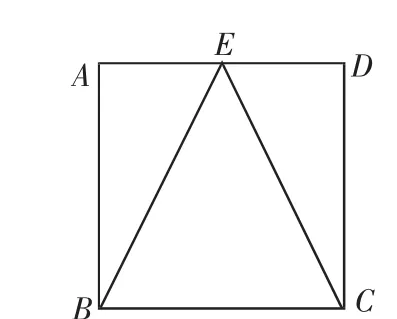
图3

评注：本题是一道简单的几何概型题目，既考查了平面几何知识，又加深了学生对概率——随机思想的理解.

无独有偶，请看例3的背景知识在中考中也曾出现过：

例4 （2001年中考杭州市卷第6题3分）如图4，在矩形ABCD中，点E是AD上任意一点，则有（ ）.

A.△ABE的周长+△CDE的周长=△BCE的周长

B.△ABE的面积+△CDE的面积=△BCE的面积

C.△ABE∽△DEC

D.△ABE∽△EBC

略解：如图4，选B.

评注：本题的结论更具有一般性，例3只是其特殊情况之一.

可供教师命制相关题目、学生学习时参考的类似结论有：

（1）如图5，△ABC的中线AD将该三角形的面积平分.

（2）如图6，三角形的重心与三角形三顶点的连线，把该三角形分成三个等面积的小三角形.

（3）如图7，过平行四边形ABCD对角线交点O的直线EF，分别与AD、BC交于点E、F，则直线EF将该平行四边形的面积平分.

图4

图5

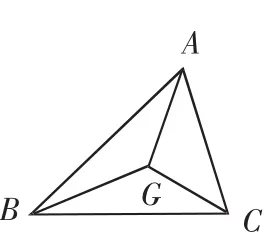
图6

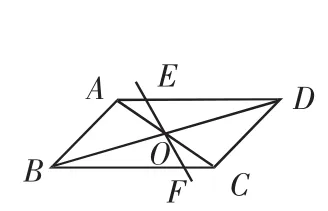
图7

（4）如图8，过梯形ABCD中位线GH中点O的直线EF，分别与AD、BC交于点E、F，则直线EF将该梯形的面积平分.

（5）如图9，过⊙O的圆心O的任意直线与该圆交于点E、F，则直线EF将该圆的面积平分.

（6）如图10，设O为任意四边形ABCD对角线AC的中点，则折线B-O-D将该四边形的面积平分.

图8

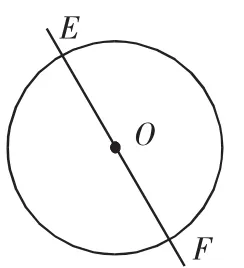
图9

图10

（7）如图11，过任意四边形ABCD对角线AC中点O的直线EF∥BD，分别与BC、CD交于点E、F，则直线BF将该四边形的面积平分.（直线BF亦被称为“好线”）

（8）菱形、矩形、正方形是平行四边形的特殊情况，（3）中的结论也成立.

（9）等腰梯形、直角梯形是梯形的特殊情况，（4）中的结论也成立.

（10）显然，对于平行四边形，两条对角线分别将该平行四边形的面积平分.

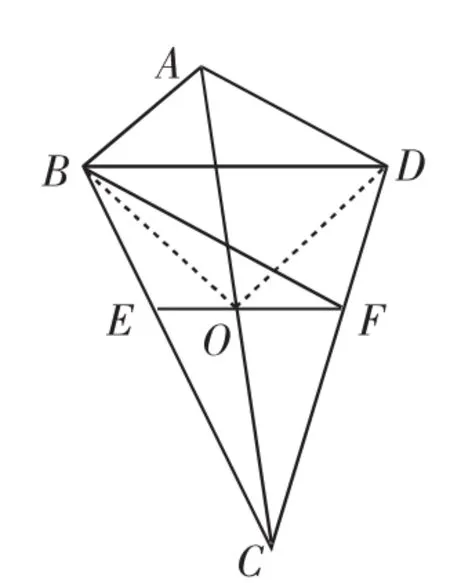
图11

1.中华人民共和国教育部制定.全日制义务教育数学课程标准（实验稿）［M］.北京：北京师范大学出版社，2001：47，49.

2.中华人民共和国教育部制定.义务教育数学课程标准［M］.北京：北京师范大学出版社，2012：119.