以表助形，规律显现——谈平面直角坐标系中有关正方形的规律探究

☉江苏省海门市能仁中学 花永平

以表助形，规律显现
——谈平面直角坐标系中有关正方形的规律探究

☉江苏省海门市能仁中学 花永平

近几年中考中，以正方形和平面直角坐标系两种元素构建的相关中考题层出不穷，它们体现出以下特点：（1）构图美观；（2）能够考查学生的探究能力；（3）具有规律性.在具体的解题过程中，如何使复杂问题简单化？如何让问题规律明晰化？表格辅助，作用不小.以近几年中考试题为例，与同行共鸣.

一、与一次函数同行

例1 （2009 年东营）正方形 A1B1C1O、A2B2C2C1、A3B3C3C2、…按图 1 所示的方式放置.点 A1、A2、A3、…和点 C1、C2、C3、…分别在直线y=kx+b（k＞0）和x轴上，已知点B1（1，1）、B2（3，2），则Bn的坐标是___________.

分析：通过求一次函数解析式，可以探索出B1、B2、B3这几个特殊点的坐标，进而借助表格探索B的坐标与正方形的序号数有怎样的关系？

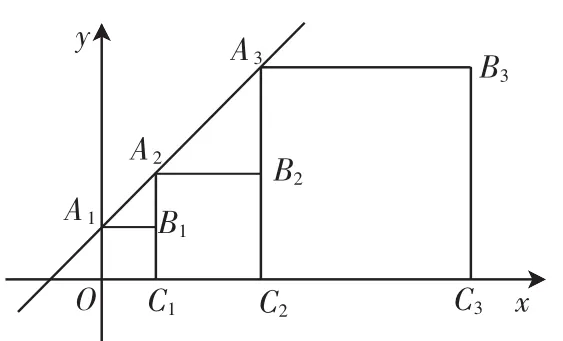
图1

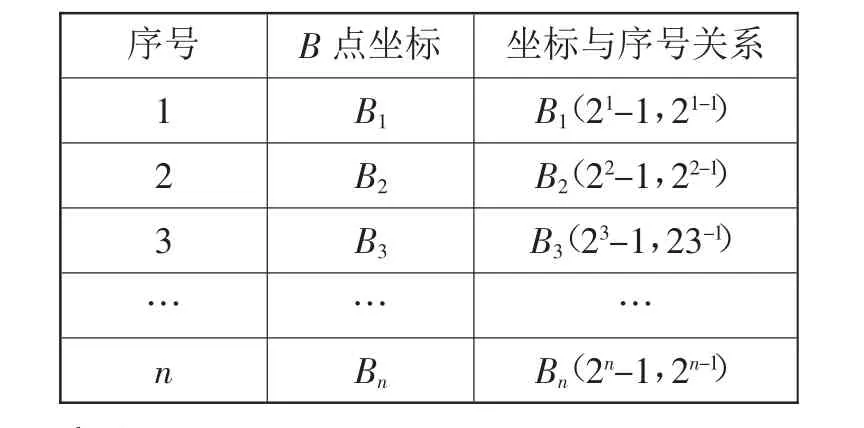
序号 B点坐标 坐标与序号关系1 B1B1（21－1，21－1）2 B2B2（22－1，22－1）3 B3B3（23－1，23－1）………n BnBn（2n－1，2n－1）

变形1

（2011年内江）在直角坐标系中，正方形A1B1C1O1、A2B2C2C1、…、AnBnCnCn-1按图2所示的方式放置，其中点A1、A2、A3、…、An均在一次函数y=kx+b的图像上，点C1、C2、C3、…、Cn均在 x 轴上.若点B1的坐标为（1，1），点 B2的坐标为（3，2），则点An的坐标为________.

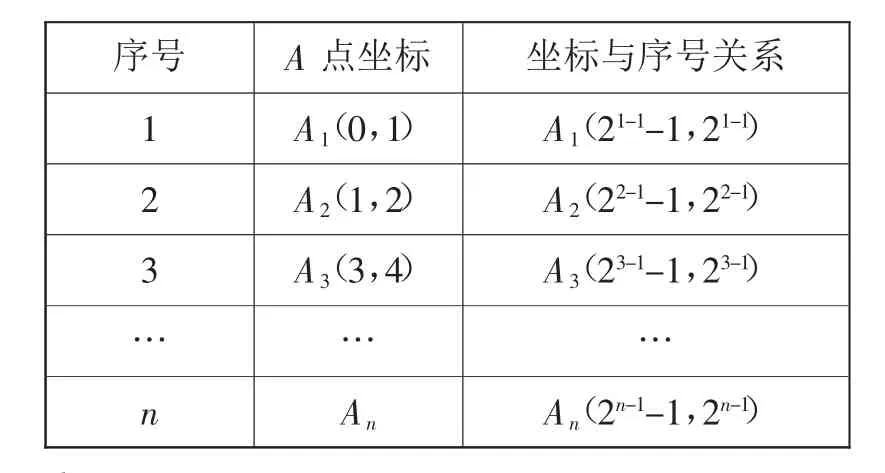
序号 A点坐标 坐标与序号关系1A1（0，1）A1（21－1－1，21－1）2A2（1，2）A2（22－1－1，22－1）3A3（3，4）A3（23－1－1，23－1）………n AnAn（2n－1－1，2n－1）

变形2

把变形 1 中“若点 B1的坐标为（1，1），点 B2的坐标为（3，2）”改为“已知正方形A1B1C1O、正方形A2B2C2C1的面积分别是1和4”，则点An的坐标为________.

分析：把面积转化为点B1、B2、…的坐标.结果同上.

变形3

把变形 1 中“若点 B1的坐标为（1，1），点 B2的坐标为（3，2）”改为“点 A1、A2、A3和点 C1、C2、C3分别在直线 y=x+1 和 x 轴上”，则点An的坐标为________.

分析：利用正方形的性质求出点A1、A2、…的坐标.结果同上.

图2

变形4

（2012 年锦州） 图 3，正方形 A1B1B2C1、A2B2B3C2、A3B3B4C3、…、AnBnBn+1Cn，按图3所示放置，使点 A1、A2、A3、A4、…、An在射线OA 上，点 B1、B2、B3、B4、…、Bn在射线 OB 上.若∠AOB=45°，OB1=1，图中阴影部分三角形的面积由小到大依次记作 S1、S2、S3、…、Sn，则Sn=________.

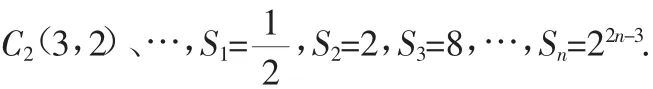
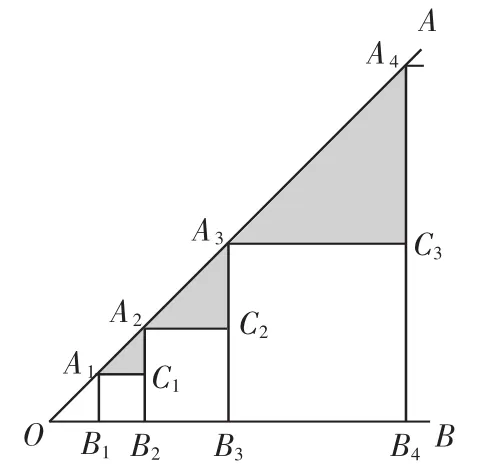
图3

变形5

将图形再做变化，在直角坐标系中，等腰直角三角形A1B1O、A2B2B1、A3B3B2、…、AnBnBn－1按图 4 所示的方式放置，其中点 A1、A2、A3、…、An均在一次函数y=kx+b的图像上，点B1、B2、B3、…、Bn均在 x 轴上.若点B1的坐标为（1，0），点 B2的坐标为（3，0），则点 An的坐标为________.

二、与拼图游戏

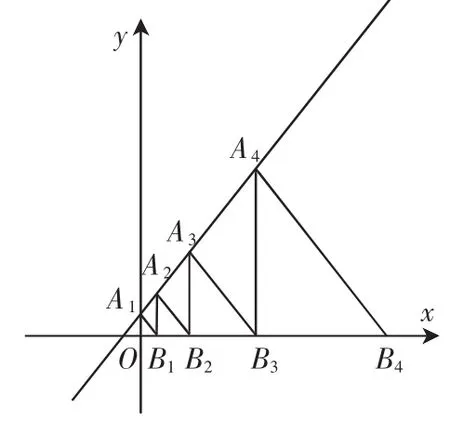
图4

例2 （2012年苏州）已知在平面直角坐标系中放置了5个如图5所示的正方形（用阴影表示），点 B1在 y 轴上，点 C1、E1、E2、C2、E3、E4、C3在 x 轴上.若正方形 A1B1C1D1的边长为 1，∠B1C1O=60°，B1C1∥B2C2∥B3C3，则点A3到x轴的距离是（ ）.

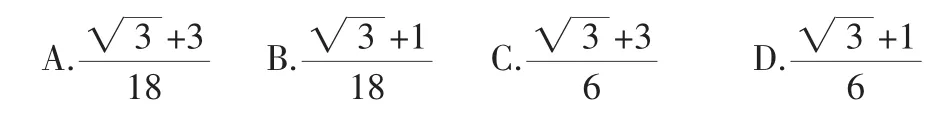
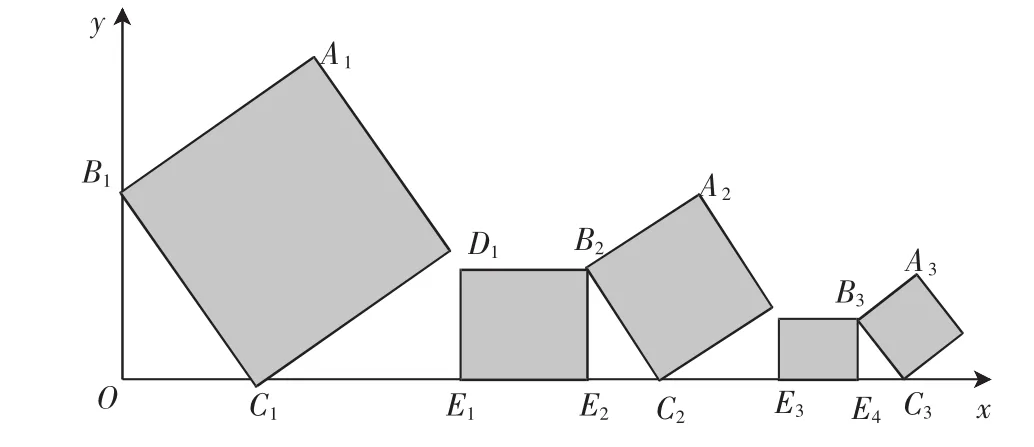
图5

分析：根据已知条件，可以证明含点A的正方形是相似的，通过计算含点A的正方形的边长及A1到x轴的距离，借助相似性质，可以表示出点A2、A3到x轴的距离，如果按照规律继续向右放置，同样可以表示出An.

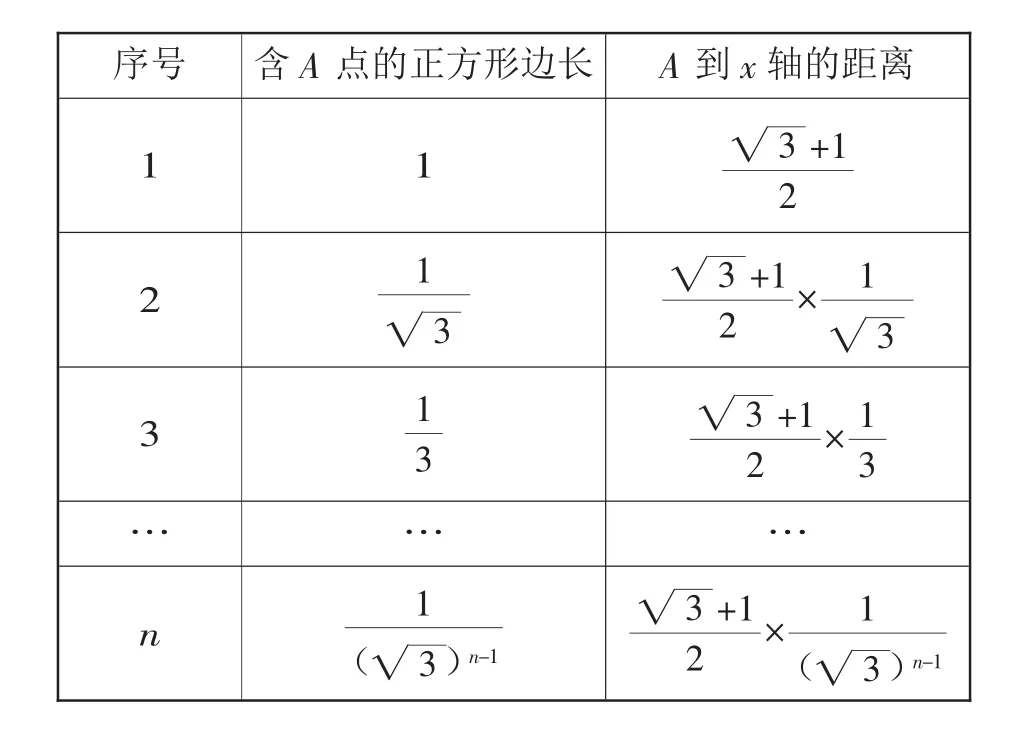
序号 含A点的正方形边长 A到x轴的距离1 1 3■ +1 2 2■ +13 1 3■2 ×1 3■1■ +1 3 3 3 2 ×1 3………1■ +1 n 3（ 3■ ）n－12×1（ 3■ ）n－1

三、与弦图镶嵌

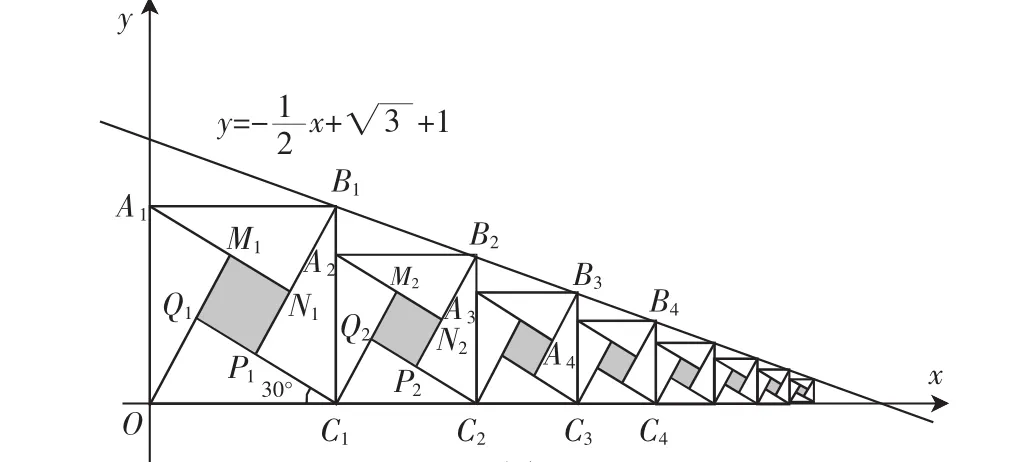
图6

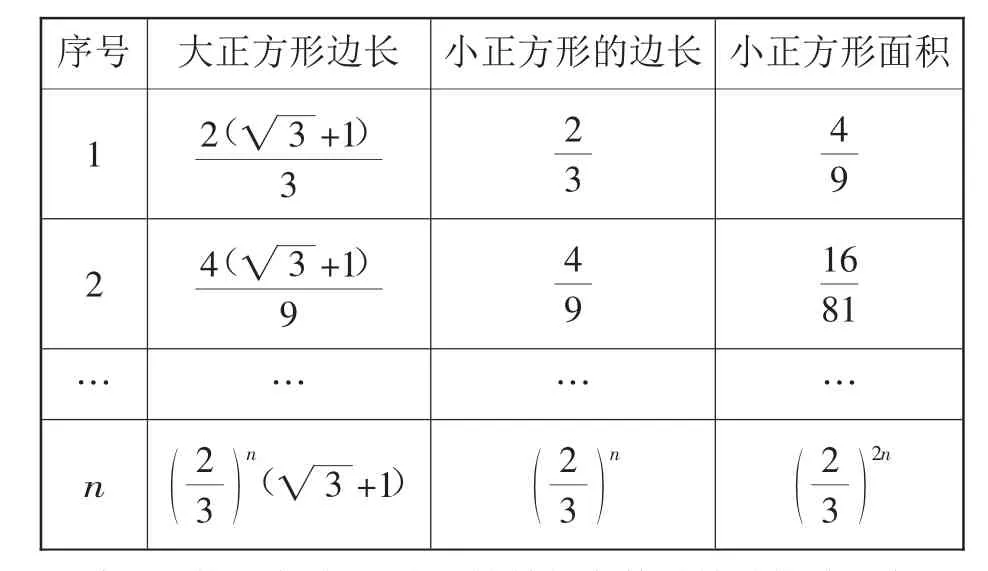
序号 大正方形边长 小正方形的边长 小正方形面积1 2（ 3■ +1）24 3 3 9 2 4（ 3■ +1）4 9 9 16 81…………n 2 3（）n（ 3■ +1） 2 3（）n2 3（）2n

通过以上的研究，提醒我们的教师在数学教学的过程中，需要关注学生的思维，拓展学生的思路，让学生找到解决问题的途径，需要培养学生用数学思想思考问题，逐步渗透数形结合思想、化归思想等，提升学生分析问题、解决问题的能力.