垂直于弦的直径的教学设计与反思

☉江苏省盐城市明达中学 徐 芬

垂直于弦的直径的教学设计与反思

☉江苏省盐城市明达中学 徐 芬

2011年版初中数学课程标准提出了初中数学教学要以“基础知识、基本技能、基本思想和基本活动经验”为目标的“四基”的要求；要求初中数学教学要处理好学习过程和学习结果、学生自主学习和教师的讲解引导、合情推理和演绎推理、生活情境和知识系统的关系.本文就“垂直于弦的直径”的教学，谈谈我的教学设计与反思.

一、教学设计

1．欣赏动画，引起注意

动画视频出示常见的轴对称几何图形，视频动画演示圆的轴对称性.

2.动手折叠，激发兴趣

学生动手折叠圆形纸片，感悟圆的轴对称性，加深印象，激发学习兴趣.

3.导入课题，明确目标

教师结合画面讲解圆是轴对称图形.再问同学们由圆的对称性能得到哪些结论，从而引出课题，明确学习目标.

4.呈现刺激，启迪思维

引导学生在圆形纸片上作垂直于弦的直径，再折叠，猜测结论.四人学习小组间可以讨论．视频动画用不同的颜色或闪烁等方式提供信息，启迪学生思维.

5.学法指导，证明定理

师生共同完成定理证明.如果发现学生证明时用全等形的知识，引导用对称的知识证明.

6.再次刺激，理解定理

题A 如图1，在⊙O中，若MN⊥AB，MN为直径，则______，_______，_______；

题B 如图2，在⊙O中，若OM⊥AB，M为垂足，则_______.

题C 小结定理要点，研究图形的性质.

7.学法指导，试用定理

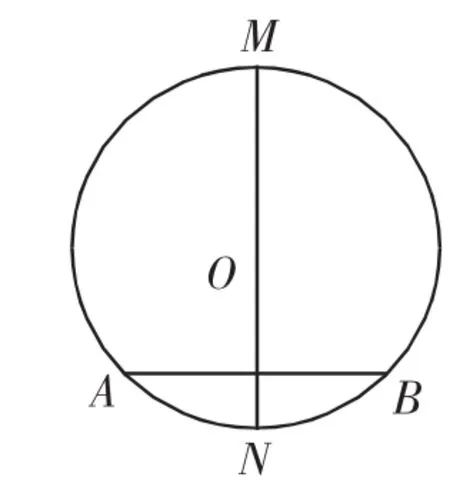
图1

图2

图3

例1 如图3，已知在⊙O中，弦AB的长为8，圆心O到AB的距离为3，则⊙O的半径是________.

8.引发行为，保持迁移（教师以题组形式给出变换练习）

题D 如图3，已知在⊙O中，弦AB的长为8，圆心O到AB的距离为3.

（1）求⊙O的半径；

（2）若点P是AB上的一动点，试求线段OP的长度的变化范围.

9.再次指导，熟用定理

例2 已知在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C、D两点.试猜测线段AC与线段BD的大小关系，并且证明你的猜想.

10.引发行为，合作探索

教师逐题呈现3个练习，其中第三题为探索性问题且需对图形分类讨沦，又构成了题组.

题E 如图4，已知CD是⊙O的直径，AB是弦，AB∥CD，AE⊥AB，BF⊥AB，垂足分别为A、B，AE、BF分别交CD于E、F.猜测线段CE与线段DF的大小关系，并且证明你的猜想.

题F 如果CD与AB不平行，其他条件不变，结论是否成立？请画出图形井说明理由.

题G 若⊙O的直径为10，弦AB平行于弦CD，AB=6，CD=8，求AB与CD的距离.

11.反馈矫正，培养思维

一学生板演题F，教师评讲，给出正确答案．教师提出有无其他解法，引发学生思维发散，对学生再一次进行学习指导.

12.评价行为，培养能力

教师给出课堂检测，对个别学生给出进一步的指导，使每个人都得到良好的数学教育，不同的人在数学上得到不同的发展.

二、教学反思

图4

我设计本节课时，引导学生观察、动手操作、猜想、合作、讨论、探究，注重知识的发生和发展过程，以题组的形式帮助学生保持、巩固、迁移知识，启迪学生思维，努力减负增效，着眼对学生学习方法的指导，提高他们学习数学的积极性.从下面四个方面做了一点尝试.

1.营造和谐课堂，激活课堂氛围

我从学生的生活经验出发，通过折纸活动引导学生去观察、动手操作、猜想，从直观感知中得出圆是轴对称图形，通过在圆纸片上作垂直于弦的直径，再折叠，引导小组讨论，观察得出结论；通过组织学生动手、观察、猜想等活动，激发学生的学习积极性，营造了和谐的课堂氛围，向学生提供了充分参与教学活动的机会，帮助他们在平等、尊重、信任中学习和掌握知识.

2.变换呈现方式，激发探究欲望

我在教学中通过视频动画演示圆的轴对称性和图形中线段的运动变化，让学生感受和欣赏数学的美，在欣赏的同时感悟知识间的内在联系，深化对所学知识理解的同时，使学生的情绪跟着动态的画面活跃起来，在应用定理解决问题时我注意一题多变，激发学生探究新知识的欲望，努力减负增效.

3.引导学生探究，加强学法指导

我坚持以人为本和以促进学生的发展为本，不是把知识直接告诉学生，而是以题组的形式，根据教学的进程依次提出所要研究的问题，逐一组织学生进行讨论和解决，加强学法指导．

4.更新教学理念，改进教学行为

我在本节课的教学过程中，时时都以学生的发展为中心，处处以促进学生的发展为本，把自己定位为学生学习的引导者、组织者、参与者、合作者，让学生充满兴趣地思考、讨论，使学生建立自信心，体验数学活动中的探索和创造过程，主动学习，获得知识，培养能力，提高数学素养.

总之，我们既要做知识的传授者，又要做学生学习的促进者，与学生共同成长.我们要加强教学反思，更新教学理念，改进教学行为，真正把一切为了学生的发展和加强“四基”教学落实到我们的平时教学过程中.