基于ICA的无线电通信干扰抑制
马俊岭, 杨保平, 尚 萌, 肖 野
(1.中国航空工业洛阳电光设备研究所,河南 洛阳 471009; 2.装备指挥技术学院,北京 101416;3.中国人民解放军63893部队,河南 洛阳 471003)
0 引言
在信息化进程中,无线通信面临越来越恶劣的战场电磁环境。通信对抗技术快速发展的同时也推动了通信抗干扰技术的发展,干扰抑制技术是其中的一个研究热点,其基本思想是接收端接收通信信号后,在进一步进行信号处理之前采取措施把通信信号中的干扰成分消除,最大限度地降低噪声对通信的影响[1]。
传统意义上干扰抑制技术主要利用干扰和通信信号的区别,在时域、各种变换域和空域有选择地滤波,进行干扰的检测和消除,保留通信信号并抑制干扰。基于时域的干扰抑制技术对于瞬变干扰信号由于算法复杂可能导致滤波器收敛慢;基于变换域的干扰抑制技术需要复杂的迭代运算;基于时域、变换域的干扰抑制技术都可能造成干扰抑制实时性差,对通信信号都有一定损伤;基于空域的干扰抑制技术可以和其他干扰抑制手段结合使用,但是设备复杂,并且在干扰和通信信号来自同一方向时无能为力。传统的干扰抑制技术存在的共同问题是对于同频干扰存在很大局限性[1]。针对这些问题,本文采用盲源分离技术[2]应用于干扰抑制领域,对干扰抑制新技术进行探索和尝试。
盲源分离经历了近20年的迅速发展,其理论和算法研究日趋完备[3-4],盲源分离技术在众多领域展现出诱人的应用潜力,成为当前信号处理前沿技术的新兴学科之一[3-6],目前盲源分离在电子战领域的应用刚刚起步[7-10]。文献[7]将单音干扰与调频电台信号进行了分离,从而抑制干扰,对可行性和有效性进行了初步分析讨论;文献[8]基于盲源分离理论对雷达抗干扰方法进行了探索,没有涉及通信领域;文献[9]利用FastICA算法对亚高斯分布的无线电通信信号进行了干扰消除,对属于超高斯分布的通信信号缺少论述;文献[10]将盲源分离技术用于对主动声纳直达波的干扰抑制。
盲源分离充分利用混合观测数据内在的统计特征提取源无线电通信信号,对源信号和传输通道参数无要求,这种独特的优势在电子对抗领域拥有广阔的应用前景。
1 算法简介
独立变量分析(ICA)是解决盲信号处理中信号分离的主要方法之一[4]。本文中涉及信息化战场无线电通信和干扰信号,物理意义上各种信号之间统计独立,可以采用ICA方法进行干扰抑制。
1.1 问题说明和信号模型
设n个信号源发出信号为 s1(k),s2(k),…,sn(k)。其中:k为离散时间变量,每个采样点均相互统计独立;S(k)=[s1(k),s2(k),…,sn(k)]T为 n×1维源信号矢量。n个源信号中1个是期望的通信信号,其他n-1个信号源是各类有意或无意干扰信号。经过多信道传输,在m个天线阵元处观测得到的混合观测信号为 x1(k),x2(k),…,xm(k),则 X(k)=[x1(k),x2(k),…,xm(k)]T,为 m ×1维混合信号矢量。则最简线性瞬时混合系统模型为

式中,A为线性瞬时混合矩阵。
盲源分离的目标就是在不知道混合矩阵A的情况下,从观测信号中分离或恢复出原始信号的过程。即求一个n×m维的解混矩阵B,使得

盲源分离问题的解决就是利用信号间统计独立性判断准则建立代价函数,求解得到矩阵B≈A-1,从混合观测信号中分离提取出源通信信号,从而抑制其他源通信或干扰信号。
1.2 基本假设
盲源分离问题实际上是一个优化问题,问题并没有唯一解,欲使盲源分离问题有意义,需作如下假设:
1)源信号之间假定是相互统计独立的,该假设是独立分量分析算法的基本出发点,近似认为各用户信息之间是统计独立的,各类战场无线电通信和干扰信号产生于不同的装备,不难理解物理意义上是互相统计独立的;
2)信号矢量S(k)为零均值并且各分量服从高斯分布的分量不超过1个,该假设中高斯分量的线性混合仍然是高斯分布,当概率密度函数服从高斯分布的源信号多于一个时,则各源信号不可分[4],例如语音信号为超高斯分布,数字调制信号为亚高斯分布[9];
3)观测数目m大于等于源信号的数量n,即m≥n,该假设中当m=n时,混合方式是适定情况,当m<n时为欠定情况(Underdeter-Mined Bases),其盲源分离的解决方法在许多文献中已有论述[11]。
1.3 信号预处理
对混合信号进行解混以前,首先进行混合信号的预处理,最常见的预处理过程有去均值化和白化[12-13]。混合观测信号经预处理后,通常能够简化盲源分离算法和改善性能,并能实现降维处理[13]。信号的预处理在ICA求解过程中具有关键的作用。
若在盲源分离信号预处理过程中混合信号经过非线性器件产生谐波等额外的信号分量,可以采用滤波器进行滤除。盲源分离前和分离后均可采用传统的频域滤波技术消除带外或谐波等干扰信号的影响,将盲源分离与传统频域滤波技术相结合,最大程度地减小干扰影响。
为满足盲源分离假设条件1),必须在分离前对观测信号矢量去除均值。观测矢量X减去其均值,用X0代替X即可。

所谓白化,即通过一定的线性变换T。

Z 满足 E(zizj)= δijQ,其中,δij为 Kronecker Delta函数。
取合适的线性变换T使Z的自相关矩阵为
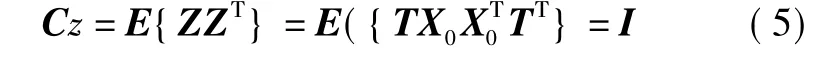
从式(5)可以看出,经白化处理后混合信号的各个信号分量之间已经失去相关性。
2 通信干扰抑制模型
经过近十几年的发展,对ICA在理论算法以及应用等诸多方面进行了积极的探索,出现了众多有价值的评判准则和算法[14-20],其中最大信噪比算法具有算法简单且运算高速的优点[12,14],首先构建信噪比代价函数,然后求解代价函数进行盲分离。
2.1 代价函数的构建
系统的输入信号为S,产生的输出信号是Y,定义二者的差E=S-Y为产生的噪声,二者的功率比为信噪比,则当信噪比取最大值时,Y就是源信号S的最优逼近,从而正确提取出源信号。根据定义可构造如下最大信噪比代价函数[15]
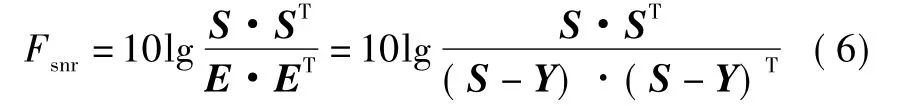
经计算简化处理,式(6)可变为[13]

2.2 算法推导
式(7)的梯度函数为

当梯度值为0时,根据定义代价函数取得最大值

3 仿真及结果分析
3.1 仿真条件
侦察天线采用4阵元圆形天线阵列,仿真只涉及基带或中频信号,其他有意或无意干扰均视为加性干扰[21]。仿真采用1路音频通信信号和3路通信干扰信号进行,通过构建的ICA通信干扰抑制模型对干扰进行抑制从而获取通信信号。仿真中,将时长为15 s的清晰音乐信号作为需要的期望信号,1路余弦单音信号,1路BPSK数字通信信号和1路宽带白噪声信号作为其他有意或无意干扰。采用Matlab 2009b进行仿真,为提高仿真效率,选取合适的采样速率和信号载频,并不影响其理论分析过程。
仿真采样率设为10 kHz,通信信号的音频主要分布在3 kHz以内,幅度范围约为1 V;余弦单载波信号的信号载频为1.6 kHz,幅度范围为1 V;BPSK通信信号载频为2 kHz,基带速率为1 kb/s,幅度范围为0.4 V。而第4路的噪声信号是标准方差为0.05的宽带白噪声干扰信号。4路源信号在时域和频域上互相混叠,时域波形如图1所示,频域波形如图2所示。

图1 源信号时域波形Fig.1 Time domain waveform of original signals

图2 源信号频域波形Fig.2 Frequency domain waveform of original signals
3.2 仿真结果分析
4路源信号经过不同信道到达接收天线阵。仿真中接收天线阵列将4路源信号混合输出,得到4路混合观察数据。混合矩阵A利用随机函数产生,混合后的时域波形如图3所示。

图3 混合信号时域波形Fig.3 Time domain waveform of mixed signals
此时对混合信号进行收听,源音频通信信号已经混杂了刺耳的单载波干扰信号、BPSK的调制噪声和嘈杂的白噪声,原来清晰悦耳的音乐声变得含混且无法忍受。
运用前面构建的基于最大信噪比算法的通信干扰抑制模型对4路源信号进行盲分离仿真,分离后的信号真实地还原了各个源信号的波形信息,分离结果见图4。图中分离结果未能提取分离信号的幅度信息,虽然分离后信号的排序与混合前相同,但并不能说明ICA能够确定信号的排序,其原因是盲源分离内在的不确定性和模糊性。这种不确定性和模糊性可视为对源信号的任意比例的收缩、排序或时滞,然而对源信号的波形信息依然保留,在实际应用中并非关键问题。
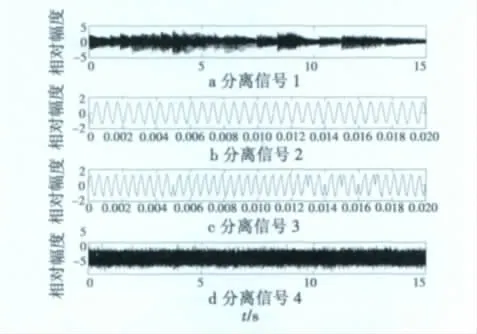
图4 分离信号时域波形Fig.4 Frequency domain waveform of separated signals
为了说明算法的性能,可用相似系数作为评价指标

当yi=csj(c为标量因子)时,ξij=1;当 yi与 sj互相独立时,ξij=0。式(10)中,分子和分母可以将标量因子c约去,从而消除幅度不确定性。当由ξij构成的相似系数矩阵每行每列有且仅有一个元素接近1,其他元素接近0,则分离的各路信号相互独立,则认为源信号得到分离。仿真中得到的相似系数矩阵为

观察相似系数矩阵,本文中基于最大信噪比算法的盲源分离的分离效果相当好。仿真算法处理15 s通信信号的运算时间约为0.75 s,而处理1.5 s的通信信号运算时间约为0.055 s,能够实时处理数据。
经过仿真将混合的加性干扰信号与源音频通信信号分离,获得了一个源音频通信信号的复制,对分离后的音频信号进行收听,其中刺耳的单载波干扰声、BPSK的切普声和嘈杂的白噪声已经消除,音质接近于源信号音质,可以认为,在接收端已经提取了期望的通信信号,抑制了信号中其他的干扰。基于盲源分离的干扰抑制技术算法简单,对信号无损伤,易采用FPGA或DSP实现。
本文讨论的方法也可用于数字通信信号的干扰抑制,例如本文中的BPSK通信信号,把BPSK信号作为期望的通信信号,而把音频通信信号作为干扰信号,同样可以实施盲源分离来进行干扰抑制。实际应用中,对收发双方的语音特征、通信频率参数等先验知识加以利用,能够更有效地提高通信干扰抑制的性能。
4 结束语
本文对基于ICA的无线电通信信号干扰抑制方法进行了分析和探讨,并结合基于最大信噪比算法的ICA进行了建模和仿真。仿真结果表明,该方法能够有效将源频谱混叠的无线电通信信号进行分离,准确地提取各源信号信息,取得了理想的分离和干扰抑制效果。未来盲源分离技术在电子战侦察、雷达、声纳、抗干扰通信、图像以及数据挖掘等领域有极大的发展应用空间。
[1] 张邦宁,魏安全,郭省道,等.通信抗干扰技术[M].北京:机械工业出版社,2006.
[2] 魏乐.基于非负矩阵分解算法进行盲信号分离[J].电光与控制,2004,11(2):38-41.
[3] 史习智.盲信号处理——理论与实践[M].上海:上海交通大学出版社,2009.
[4] HYVARINEN A,KARHUNEN J,OJA E.Independent component analysis[M].New York,USA:Wiley,2001.
[5] 杨琳,陈利平,王芝刚.独立分量分析在驾驶舱话音记录器背景信号分离中的应用[J].电光与控制,2010,17(2):68-73.
[6] 杨小牛.从软件无线电到认知无线电,走向终极无线电——无线通信发展展望[J].中国电子科学研究院学报,2008,3(1):1-7.
[7] 黄高明,杨绿溪,何振亚.一种基于盲源分离的雷达抗干扰技术[J].电路与系统学报,2004,9(6):49-51.
[8] 刘庆敖.基于盲源分离的同道数字通信干扰抑制[J].电子设计工程,2009,17(5):94-99.
[9] 高洁,李磊,刘云涛,等.主动声纳直达波干扰抑制的盲分离算法[J].声学技术,2009,28(4):537-540.
[10] 杨福生,洪波.独立分量分析的原理与应用[M].北京:清华大学出版社,2006:63-89.
[11] KIM S G,YOO C D.Underdetermined blind source separation based on subspace representation [J].IEEE Transactions on Signal Processing,2009,57(7):2604-2614.
[12] 马建仓,牛奕龙,陈海洋.盲信号处理[M].北京:国防工业出版社,2006.
[13] CICHOCKI A,SHUN-ICHI A.Adaptive blind signal and image processing[M].Revised and Corrected Edition,New York:John Wiley & Sons,2003.
[14] MA Jiancang,ZHANG Xiaobing.Blind source separation algorithm based on maximum signal noise ratio[C]//First International Conference on Intelligent Networks and Intelligent Systems,2008:625-629.
[15] 张小兵,马建仓,陈翠华,等.基于最大信噪比的盲源分离算法[J].计算机仿真,2006,23(10):72-75.
[16] SHI Zhenwei,JIANG Zhiguo,ZHOU Fugen.A fixedpoint algorithm for blind source separation with nonlinear autocorrelation[J].Journal of Computational and Applied Mathematics,2009,223(2):908-915.
[17] LENG Juxin,ZHANG Yang,TANG Bin.Estimation of source number by high-order cumulation in undetermined blind source separation [J].Modern Electronics Technique,2009,32(17):49-52.
[18] OZEROV A,F'EVOTTE C.Multichannel nonnegative matrix factorization in convolutive mixtures for audio source separation[J].IEEE Trans on Audio,Speech and Lang,2010,18(3):550-563.
[19] MENG C,TUQA J,DING Z.A quadratic programming approach to blind equalization and signal separation[J].IEEE Transactions on Signal Processing,2009,57(6):2232-2244.
[20] 李虎雄,黄琛泽.基于最大信噪比的盲源分离算法的修正与比较[J].计算机工程,2009,35(11):202-204.
[21] 杨保平,陈永光,崔博.基于盲源分离的数字通信抗干扰技术[J].通信技术,2011,44(4):5-9.

