部附件送修费用的偏最小二乘回归模型及敏感性分析

王卓健， 饶学军， 沈安慰， 贾林通

(1.空军工程大学航空航天工程学院，西安 710038; 2.西安飞机工业(集团)有限公司技术中心，西安 710089)

0 引言

长期以来，飞机维修费用的估算是热点也是难点。维修费用涉及因素复杂，持续时间长，使得在飞机寿命周期费用中，维修费用是其主要构成成分［1］。根据WATOG(World Airline Technical Operations Glossary)对维修费用的划分标准，可分为直接维修费用和间接维修费用，间接维修费用由于与管理因素有关，难以在设计阶段考虑。

目前，国内外研究主要集中在直接维修费用上，已经形成了一些方法和体系［2］。国外已经有较为成熟的寿命周期费用估算软件，最具有代表性的当属PRICE(Parametric Review of Information for Costing and Evaluation)，它在国外应用中取得了较好的效果［3］。但是，由于国内与国外在经济体制、费用发生状况上有较大区别，完全照搬并不适合我国国情。利用目前掌握的数据，开发出一套适合国情的费用模型已势在必行。部附件的送修费用在整个直接维修费用中占有基础性地位并且费用数据相对透明，因此构建部附件送修费用模型不失为一个好的突破口。在部附件送修费用模型中，较为著名的是波音的可信性成本(DCM)模型［4］和空客公司的模型。这两种模型所需的输入数据涉及到人工时费用和材料费用，这些数据很难在国内收集到。文献［5］针对这两种模型在国内应用的难点，提出了基于免疫粒子群算法的组合预计，但是此模型的输入参数是通过某些设计性能参数估算得出，数据的准确性不能保证。同时，由于其组合模型的“黑匣子”特性，与其他一些智能预测方法，如神经网络［6］，支持向量机［7］等一样，虽然预测精度较高，但同样存在不方便进行敏感性分析的缺点。偏最小二乘回归由于在处理小样本多元数据具有优越性，并且能方便进行敏感性分析，已经应用到机体研制费的估算上，取得了较好的效果［8］。本文针对目前国内数据特点提出了一种基于偏最小二乘回归的部附件送修费用的参数模型，并进行了敏感性分析。

1 数据收集与处理

全寿命费用的定量研究方法主要有类比法、工程估算法、参数法，其中参数法的研究最为广泛和流行［9］。要建立一个较好的参数模型，首先根据可收集到的数据，包括各种参数数据和费用数据，筛选出与费用关系密切的参数;其次，利用一种建模理论，建立费用与参数之间的函数关系。其中关键在于所收集数据的准确性，本文收集到了某型飞机20种部附件的数据，包括有重量(W)、体积(V)、价格(P)、平均非计划拆卸时间(TMTBUR)，平均车间修理时间(TST)，SRU的个数(NSRU)以及送修费用(PS)等，如表1所示。

表1 部附件参数与送修费用Table 1 Parameters and repair cost of components

续表

2 变量投影重要度分析

基于表1，可选取偏最小二乘回归［10］来建立参数模型。首先筛选参数，常用的方法有相关关系分析、变量逐步回归法等，这些方法在小样本情况下面临新的困难，而基于偏最小二乘回归的变量投影重要度分析是一种有效方法。

根据文献［10］，可以做如下表述。参数对因变量的解释能力是以变量投影重要性指标Pj(Variable Importance in Projection)来测度的。其定义式为

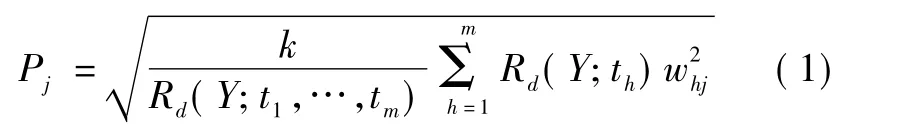
式中:whj为轴wh的第j个分量，用于衡量xj对构造th主成分的贡献大小;Rd(Y;th)和 Rd(Y;t1，t2，…，tm)分别为Y由th和t1，t2，…，tm所解释的变异精度(测定系数)，分别代表了th对Y的解释能力和t1，t2，…，tm对Y的累计解释能力。

式中，r(Y，th)是因变量Y和主成分th的相关系数。

Pj定义式的意义是基于这样一个事实:由于xj对Y的解释是通过th来传递的，如果th对Y的解释能力很强，而xj在构造th时又起到了相当重要的作用，则xj对Y的解释能力就被视为很大。也就是说，如果在Rd(Y;th)值很大的th成分上，whj取很大的值，则xj对解释Y就有很重要的作用。

另外，因为有

所以，对于k个参数xj(j=1，2，…，k)，如果在解释 Y时的作用都相同，则所有的Pj均等于1;否则，对于Pj＞1的xj，在解释Y时就有更加重要的作用。

根据式(1)～式(3)，将重量、体积、价格、平均非计划拆卸间隔时间、平均车间修理时间、SRU的个数当作参数，将送修费用作为因变量，提取一次主成分，计算其变量投影重要度，得到结果如表2所示。

表2 6个参数的变量投影重要度Table 2 The VIP of six parameters

从表2可以看出，体积的变量投影重要度值过于偏小，因此可以删除体积重新计算各个参数的变量投影重要度，如表3所示。

表3 5个参数的变量投影重要度值Table 3 The VIP of five parameters

从表3可以看出，没有变量投影重要度值明显偏小的参数，且比较均衡，因此保留现有5个参数。

3 偏最小二乘回归模型

采取文献［10］的建模方法，选取重量、价格、平均非计划拆卸间隔时间、平均车间修理时间、SRU的个数为参数开始偏最小二乘回归建模。采用对数线性关系式，取第一主成分，此时变量投影重要度较为均衡，拟合公式为

当给定显著性水平 α为0.01，t检验的值 T为1.0577，接受 t检验;当假设检验参数 F 为 1.9578，接受F检验。将式(4)进一步作标准化的逆过程，则可以得到

式(5)的平均误差为3.53%，不需要进行第二主成分的提取。误差如图1所示。

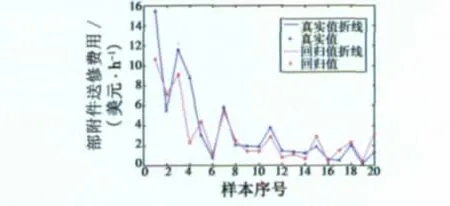
图1 真实值与回归值的误差Fig.1 The error of the true number and regression number

4 部附件维修费用敏感性分析

得到了部附件送修费用的偏最小二乘回归模型后，可以方便进行费用敏感性分析。在工程设计时要求部附件送修费用最小，则重量、价格、平均车间修理时间、SRU的个数是越小越好，平均非计划拆卸间隔时间越大越好。根据工程经验，假设其参数的取值范围如表4所示。

表4 5个参数的取值范围Table 4 The range of five parameters

在各个参数值由最差值向最优值逼近的过程中，设计人员最为关心的是费用变化最为敏感的区间。当重量W变化时，其他参数值保持最差值不变时，其重量与部件送修费用的单一函数为

其重量与部附件送修费用变化曲线如图2所示。

图2 重量与送修费用关系Fig.2 The relation of weight and repair cost

敏感度实质上就是重量与费用关系曲线上各个点的切线斜率，根据切线曲率即为单一函数一阶导数的事实，对式(6)求一阶导数

将重量的数值代入式(7)计算，可以得到曲线在某一点上的切线斜率，即为敏感度。在重量与送修费用的敏感度分析中，重量由最差值(40)向最优值(0)逼近的过程中(步长单位选择为0.1)，敏感度在［0.2019+∞］之间变化。重量与敏感度的关系曲线如图3所示。

图3 重量与敏感度关系Fig.3 The relation of weight and sensitivity

本文认为对于重量而言，敏感度大于1时，即属于显著敏感性区间。同理可以得到其他参数对应的送修费用单一函数表达式，显著敏感性区间以及所对应参数范围，如表5所示。

表5 显著敏感性区间以及所对应参数范围Table 5 The salient sensitive interval and the range of parameter

价格、平均非计划拆卸间隔时间、平均车间修理时间、SRU的个数与敏感度之间的关系曲线如图4～图7所示。

图4 价格与敏感度关系Fig.4 The relation of price and sensitivity

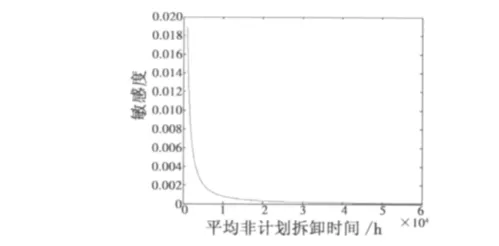
图5 平均非计划拆卸间隔与敏感度关系Fig.5 The relation of MTBUR and sensitivity

图6 平均车间修理时间与敏感度Fig.6 The relation of the mean shop repair time and sensitivity

图7 SRU数量与敏感度Fig.7 The relation of the number of SRU and sensitivity

5 结论

本文根据所收集到的某型飞机部附件的参数及送修费用数据，建立了基于重量、价格、平均非计划拆卸间隔时间、平均车间修理时间、SRU的个数为参数的部件送修费用偏最小二乘回归模型，模型平均误差小于5%，由于采取了对数线性表达式，复杂程度大大降低，完全可满足工程实践的需要，结合模型，利用切线斜率的物理意义详细计算了单一函数模型的显著敏感性的区间。计算表明，显著敏感性区间与参数的最差值和最优值有较强的相关性。需要特别注意的是计算敏感度时，每个参数在工程实际中递增或递减的单位量级(如价格变化的单位是100美元还是1000美元，可能不同的部件并不完全相同)，此问题并没有在文中探讨，需要进一步的实际数据支持和研究。

［1］ 张恒喜，郭基联，董彦非，等.现代飞机效费分析［M］.北京:航空工业出版社，2001.

［2］ 陈勇.民用飞机维修成本分析与评估［D］.南京:南京航空航天大学，2006.

［3］ 郭基联，虞健飞，任建军.装备寿命周期费用估算软件PRICEH 剖析［J］.装备指挥学院学报，2009，20(4):22－26.

［4］ MEADOWS T A.Analysis of F/A －18 engine maintenance costs using the boeing dependability cost model［M］.Washington:Naval Postgraduate School Monterey，California，1994.

［5］ 吴静敏.民用飞机全寿命维修成本控制与分析关键问题研究［D］.南京:南京航空航天大学，2006.

［6］ 郭风，李登科，张恒喜，等.军用无人机研制费用的RBF神经网络预测［J］.电光与控制，2005，12(6):60－62.

［7］ 钟诗胜，付旭云，胡淑荣.小样本条件下航空装备费用预测［J］.哈尔滨工业大学学报，2011，43(5):52－55.

［8］ 王礼沅，郭基联，张恒喜.递阶偏最小二乘回归在飞机研制费用预测中的应用［J］.航空学报，2009，30(8):1380－1384.

［9］ 孟科，张恒喜，段经纬，等.基于未确知数理论的装备全寿命费用定性估算方法［J］.电光与控制，2005，12(6):66－69.

［10］ 王慧文，吴载斌，孟洁.偏最小二乘回归的线性与非线性方法［M］.北京:国防工业出版社，2006.