凸优化理论在非线性滚动时域控制中的应用
王建宏, 朱永红, 肖 绚, 唐得志
(1.景德镇陶瓷学院机电学院,江西景德镇 333403; 2.南京航空航天大学自动化学院,南京 210016)
0 引言
传统的最优控制包含有限时域和无限时域,通常反馈控制系统应该运行于充分长的时间周期中,如电力系统和化学过程。在这些实时过程中,不能采用有限时域最优控制而应使用无限时域最优控制。为此基于最优控制理论,提出了一种新颖的控制策略——滚动时域控制(RHC)。RHC的理论思路为[1]:假设在当前时刻可获得一个最优控制序列,可能是在一个有限固定时域中的闭环形式或开环形式。在整个固定时域的最优控制系列中,仅取序列中的第一个元素作为当前时刻的控制率。当状态空间形式中的状态可获得时,RHC通常利用状态反馈控制来表示。然而系统的全状态信息并不能获得,因为对所有状态的观测或估计是不可能的,同时也是非常耗费精力和物力的。
在系统辨识和控制器设计过程中经常对一目标函数进行最优化运算得到未知参数估计值,其优化的计算过程较多地采用牛顿法、拟牛顿法、高斯法和共轭梯度法[2]。根据具体的模型结构及优化函数表达式,可对上述方法进行改进,以使得优化算法较快地收敛到全局最优值。
1 滚动时域控制基本原理
滚动时域控制在每一采样离散时刻,用系统的当前状态作为初始条件,在线求解一个有限时域开环最优控制问题,得到最优控制序列[3]。并在该时刻,仅取最优控制序列过程中的第一个控制信号实际作用到系统中。在下一采样时刻,重复以上过程,此过称随着时间的推进反复滚动进行。对于含状态约束以及输入约束等限制条件的系统,滚动时域控制是一种有效的控制方法。滚动时域预测控制的基本原理可概括为以下3点:预测模型、滚动优化和反馈校正。这3点的组合是预测控制区别于其他控制方法的基本特征,同时也是预测控制在实际工程应用中取得成功的技术关键。其通用的结构如图1所示,其中,M为输入的控制过程。
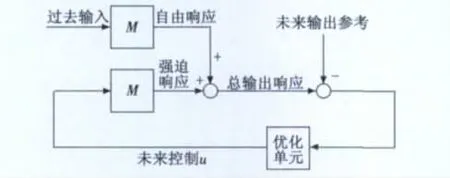
图1 滚动时域预测控制的基本结构Fig.1 The basic structure of RHC
1.1 预测模型
预测模型的功能是根据对象的历史信息和未来输入来预测其未来输出的,因此状态方程、传递函数这类传统的模型都可以作为预测模型[4]。对于线性稳定对象,甚至阶跃响应、脉冲响应这类非参数模型,也可直接作为预测模型使用。此外,非线性系统、分布参数系统的模型,只要具备上述功能,也可在对这类系统进行预测控制时作为预测模型使用。
预测模型具有显示系统未来动态行为的功能,对于不同的控制策略可用预测模型计算出不同的输出预测轨迹,从而作为选择最优控制策略使系统某个性能指标优化的基础。
1.2 滚动优化
预测控制是一种基于优化的控制算法,它是通过某一性能指标的最优来确定未来的控制作用[5]。这一性能指标涉及到系统未来的行为,例如,通常可取对象输出在未来的采样点上跟踪某一期望轨迹的方差为最小;但也可取更广泛的形式,例如要求控制能量为最小而保持输出在某一给定范围内等。性能指标中涉及到的系统未来的行为,是根据预测模型由未来的控制策略决定的。
需要强调的是,预测控制中的优化与传统意义下的离散最优控制有很大的差别,这主要表现在预测控制中的优化通常是一种有限时段的滚动优化。在每一采样时刻,优化性能指标只涉及到从该时刻起到未来有限的时间内,而到下一采样时刻,这一优化时段向前推移一个时刻点。因此,预测控制不是用一个对全局相同的优化性能指标,而是在每一时刻有一个相对该时刻的优化性能指标。不同时刻优化性能指标的相对形式是相同的,但其绝对形式是不同的。因此在预测控制中,优化不是一次离线进行的,而是反复在线进行的,这就是滚动优化的含义,也是预测控制区别于传统最优控制的根本点。滚动优化过程如图2所示。
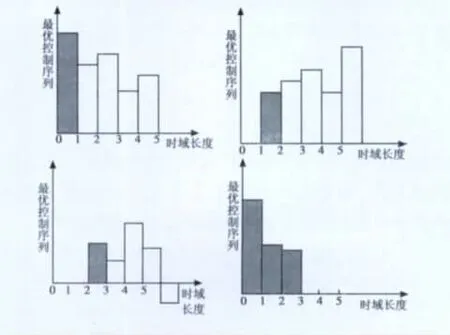
图2 滚动时域优化原理Fig.2 The principle of RHC optimization
1.3 反馈校正
预测控制是一种闭环控制算法。在通过最优确定了一系列未来的控制作用后,为了防止模型失配或环境干扰引起控制对理想状态的偏离,预测控制只实现当前时刻的控制作用。到下一采样时刻,首先检测对象的实际输出,并利用这一实时信息对基于模型的预测控制进行修正,然后再进行新的优化。
反馈校正的形式可以在保持预测模型不变的基础上,对未来的误差做出预测并加以补偿,也可以根据在线辨识的原理直接修改预测模型。预测控制都把优化建立在系统实际的基础上,并力图在优化时对系统未来的动态行为做出比较准确的预测。因此,预测控制中的优化不仅基于模型,而且利用了反馈信息,因而构成了闭环优化[5-6]。
本文以研究非线性系统的滚动时域控制是否存在最优解进行展开分析,利用凸优化理论中的基本知识分别推导出此最优化问题在无和有集合约束条件下存在最优解的充要条件,并将此充要条件与经典优化理论中现有的FJ最优条件进行对比,得出该充要条件的优势。
2 基于凸优化的最优解判定准则
利用凸优化理论中的拉格朗日乘子和最优性的KKT[7](Karush-Kuhn-Tucker)或 FJ(Fritz John)来考虑非线性系统滚动时域控制的最优解存在问题的充要条件。
2.1 非线性系统中优化问题的描述
考虑如下的非线性模型
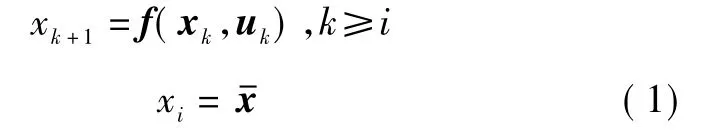
式中:f:Rn×Rm→Rn,为一给定的非线性函数;x∈Rn,为系统的状态;u∈Rm,为系统的控制输入;i为系统的初始时刻。在优化问题中,式(1)通常称为等式约束。同样,可增加关于对系统状态和系统控制输入的约束条件,此类约束条件通常是以集合约束的形式出现。
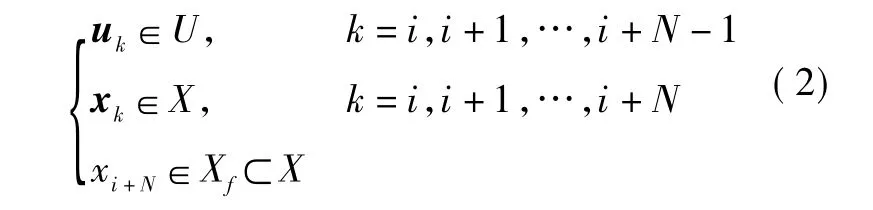
式中:U⊂Rm,X⊂Rn,Xf⊂Rn称为对应的集合;N 为优化时域水平。通常取U为紧集,X和Xf均为闭集。非线性系统的滚动时域控制可归纳为如下的最优化问题

式中:{xk}={xi,…,xi+N},{uk}={ui,…,ui+N-1}分别称为状态和控制输入序列;VN({xk},{uk})为优化问题的目标函数
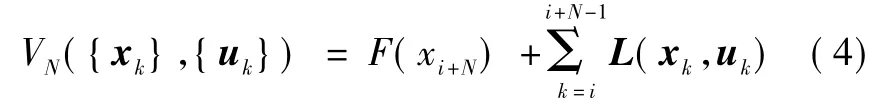
式中:F(xi+N)为关于终端状态的加权项;L(xk,uk)为关于中间状态和控制输入的连续函数。此处用一般形式来表示F和L,而不采用二次式的特殊形式。从式(4)中可知:约束条件有两种,一种为等式约束,另一种为集合约束,而集合约束可转化为一簇线性矩阵不等式。
2.2 无集合约束时的最优性条件
假设目标函数和状态方程不显式地依赖时间(即各个表达式不是关于时间的显函数,时间以隐函数的形式出现在表达式中)。令初始时刻i=0,在无集合约束时的最优化问题为

式中,{xk}={x0,…,xN},{uk}={u0,…,uN-1},f:Rn×Rm→Rn,L:Rn×Rm→R 为关于各自变量的可微函数。为了利用最优化理论中的FJ和KKT最优充要条件来推导式(5)的最优状态}和最优控制输入,定义一新的变量
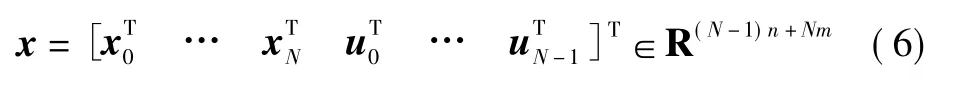
矢量x中包含了最优化问题中所有的优化变量,利用定义的优化矢量x可将式(5)中的状态方程合并为一个(N+1)n阶的矩阵约束
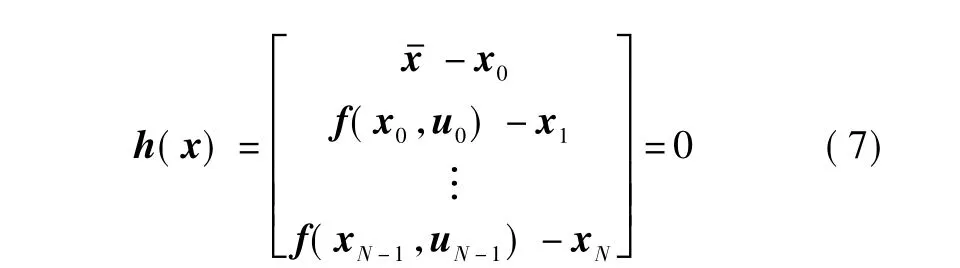
根据 xk,uk和 f(xk,uk)的维数可令
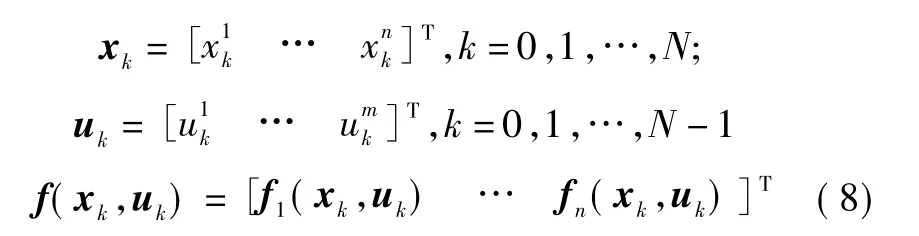
定义一阶的雅可比矩阵为
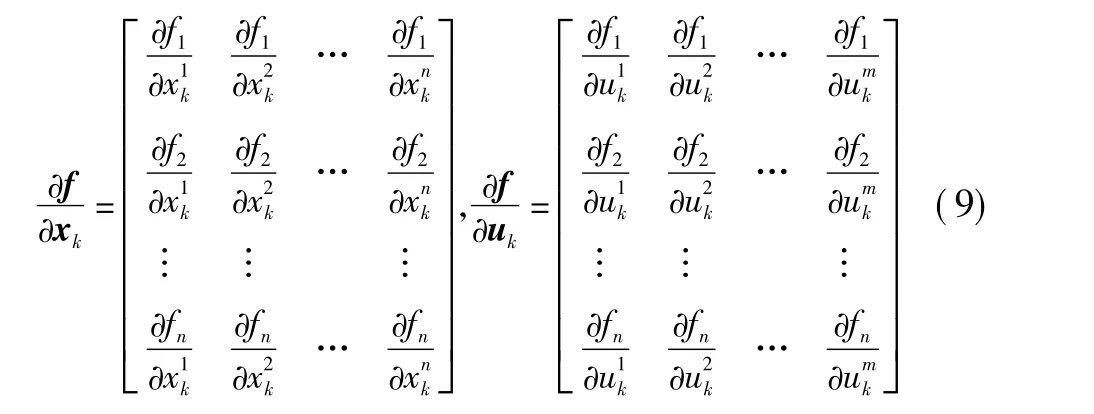
根据h(x)的构造方法,可计算矢量值函数h(x)的(N+1)n×[(N+1)n+Nm]阶的雅可比矩阵为

对于初始状态约束方程引入拉格朗日乘子λ-1∈Rn,而对于状态方程也引入拉格朗日乘子 λk,{λk}={λ0… λN-1},λk∈Rn,构造实值的拉格朗日函数为[8]
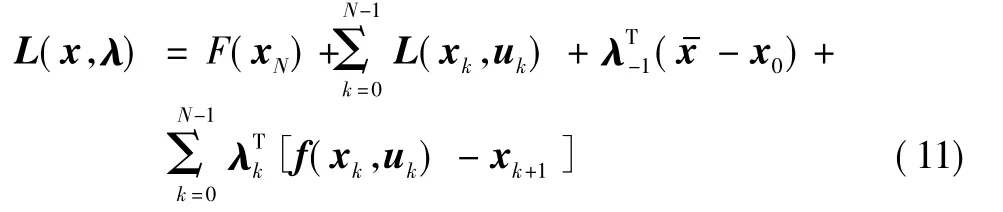
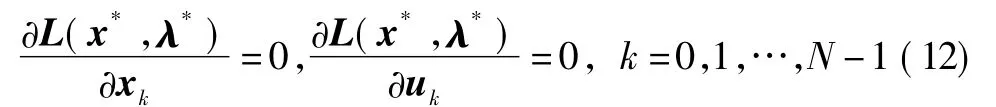

在计算偏导之前,引入一个哈密尔顿函数H:Rn×Rm×Rn→R 为
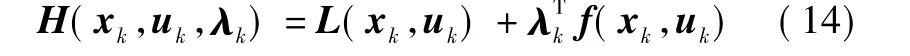
式中:L(xk,uk)为目标函数中的各步加权;f(xk,uk)为状态方程右边的矢量值函数。因
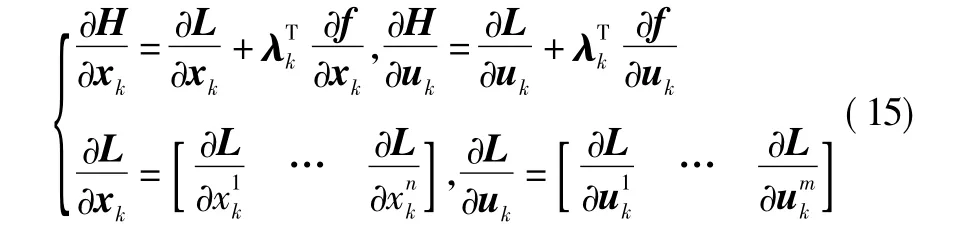
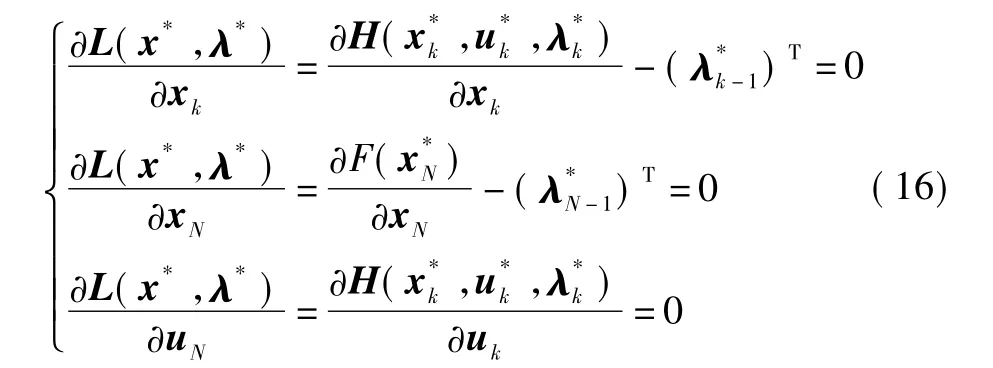
式中,k=0,1,…,N -1。
由式(16)可得,无集合约束最优化问题存在最优解的充要条件,为定理1。
定理1在无集合约束下的式(5)中,最优序列,和存在的充要条件为存在一个最优拉格朗日乘子矢量使得以下各式成立。
1)状态方程。
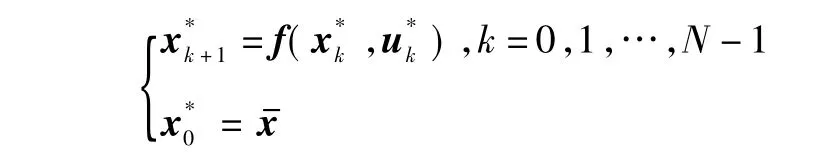
2)伴随方程。
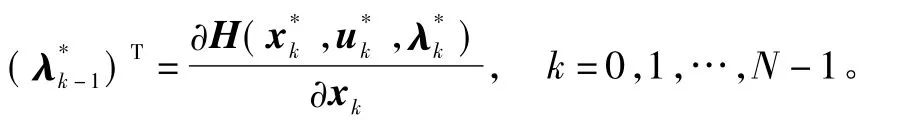
3)边界条件。
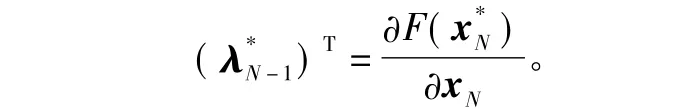
4)哈密尔顿条件。
2.3 集合约束时的最优性条件
集合约束下的最优化问题可归纳为

同样有{xk}={x0,…,xN},x∈Rn;{uk}={u0,…,uN-1},u∈Rm分别为状态和控制序列;U为关于控制输入的给定约束集;hN:Rn→Rl为关于终端状态xN的矢量值函数。对式(17)所示的最优化问题,需要施加如下的假设条件:
1)函数F(x)为二次连续可微函数;
2) 对任意的 u∈U,函数 f(x,u)和 L(x,u)为对变量x的二次连续可微函数;
3)终端约束条件hN(x)为二次可微函数,且满足对所有x∈Rn都有其雅可比矩阵是行满秩;
类似于无集合约束时的最优化问题,定义如下的哈密尔顿函数
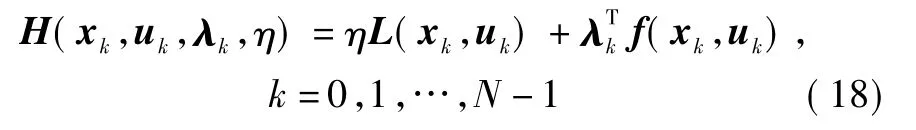
式中:η 为一实数;λk,k=0,1,…,N -1 为 Rn中的某个矢量。类似可得在集合约束条件下最优解存在的充要条件,为定理2。
定理2对于集合约束下的最优化问题式(17),存在最优序列和的充要条件是存在一个矢量序列及一个实数 η*,使得以下条件都成立。
1)伴随方程。
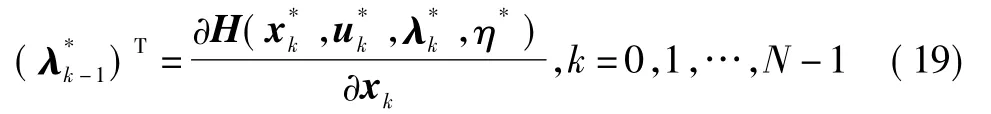
2)边界条件。存在实数β≥0和矢量γ∈Rl使得
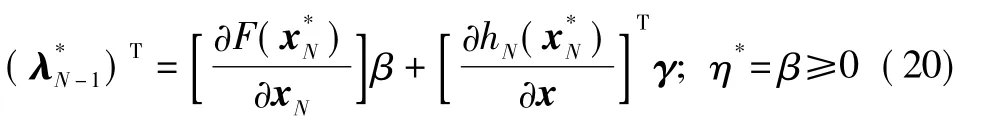
3)哈密尔顿函数的最小化。
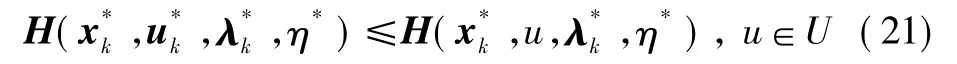
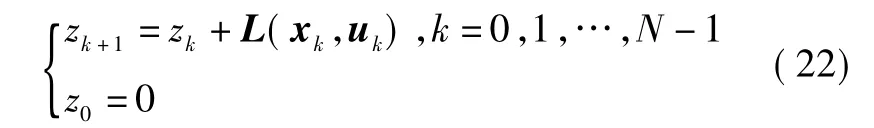
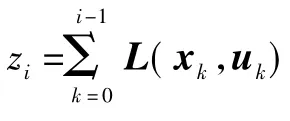
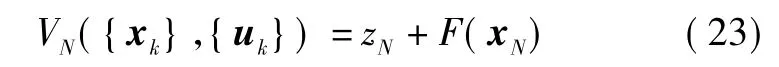
复合状态 ξk的初始状态 ξN应属于集合{ξ∶。需要最小化的目标函数式(23)改写为仅关于终端状态 ξN的函数,即:VN({xk},{uk})=zN+F(xN)=g0(ξN)。
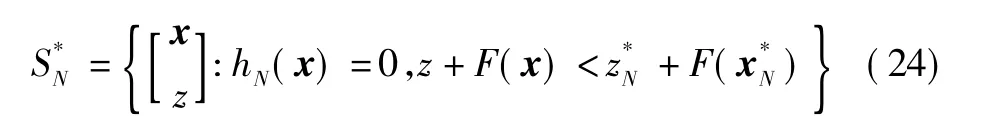
对于非线性系统,将非线性函数f(x,u),L(x,u)和hN(x)分别都在最优序列处进行线性化得到非线性方程的线性近似表达式[9],即考虑
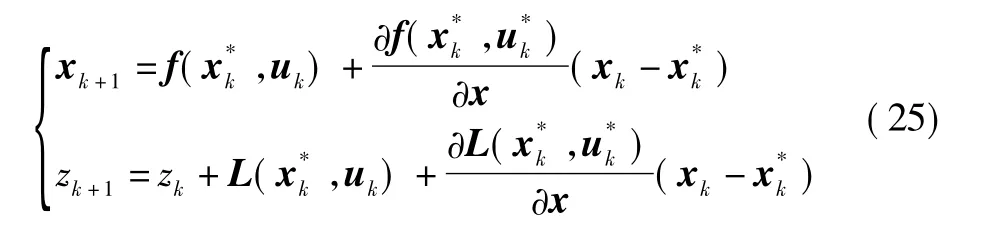
对应的约束条件为
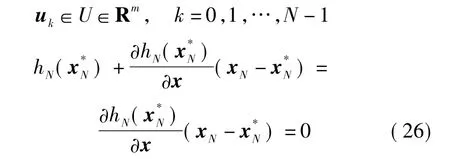
目标函数为

利用凸优化理论中的分离定理可知[10]:两集合和在点处存在一个超平面以达到分离。即存在一个非零矢量使得
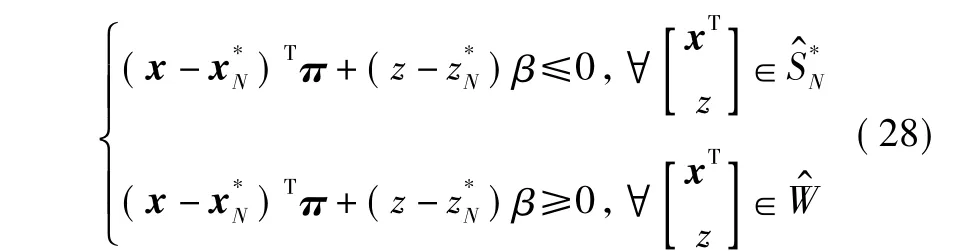
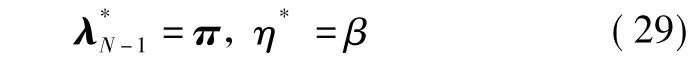
由η*=β可见,定理2中的式(19)明显满足。又由式(29)知,因,即不全为 0 。联合式(28)和式(29)得
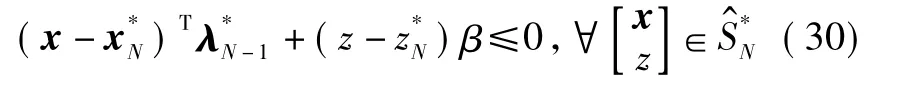
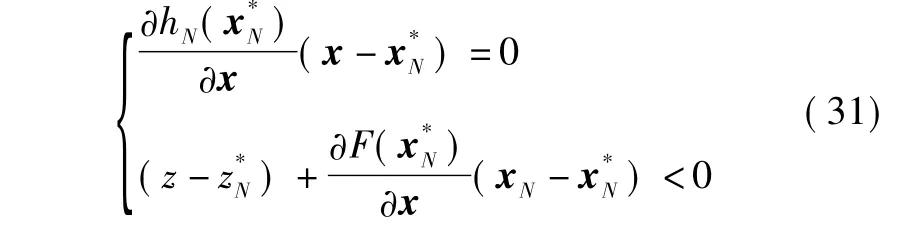
根据定义的3个矩阵将式(30)和式(31)合并为A1d<0,A2d=0。根据凸优化理论中的FJ最优性充要条件可知,存在一个非零矢量[qTνT]T,q∈R2,ν∈Rl,q >0,使得
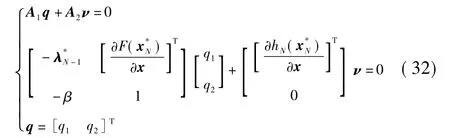
式(32)包含着
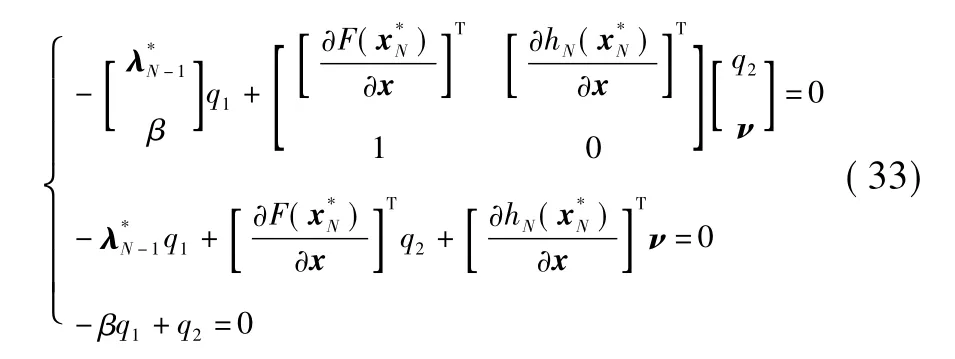
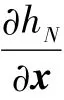

至此给出了在有或无集合约束条件下最优化问题存在最优解的充要条件,而最优化问题的求解可通过文献[11]中的椭球优化算法来求解。在求解最优控制输入序列时仅取序列中的第1个元素作用于实际的系统(线性或非线性)。联合上述的优化过程和选取第1个元素的过程为本文陈述的滚动时域预测控制方法,考虑将上面的推导过程与直接应用经典优化理论中的相关最优性条件进行比较。
2.4 最优性条件的比较
考虑如下的最优化问题
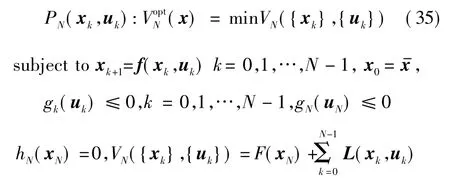
式中:{xk}={x0,…,xN},x∈Rn,{uk}={u0,…,uN-1},u∈Rm分别称为状态和控制输入序列;xk+1=f(xk,uk)为状态方程为初始状态;不等式gk(uk)≤0,k=0,1,…,N -1,gk:Rm→Rr,表示控制输入uk满足的条件,此处用线性矩阵不等式替换前面的集合约束uk∈U;gN(uN)≤0,表示对终端状态的不等式约束;hN:Rn→Rl表示对终端状态的等式约束。以下直接利用FJ最优条件推导出最优化问题式(35)存在最优序列和的最优条件。

其中各个量为
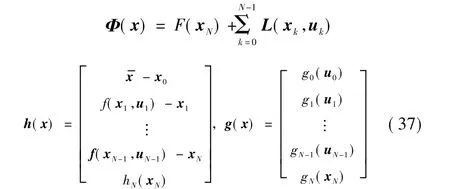


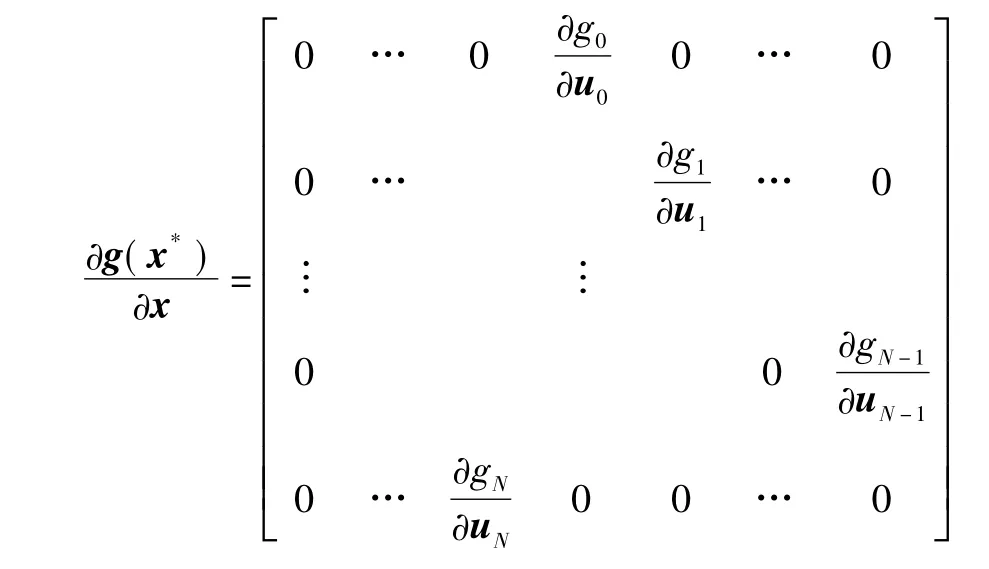
哈密尔顿函数定义为
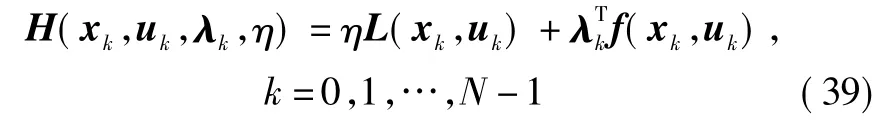
根据凸优化理论中的对偶可行条件或FJ条件可得定理3。
定理3原优化问题存在最优解的充要条件是存在一标量 η*和矢量满足如下的条件。
1)伴随方程。
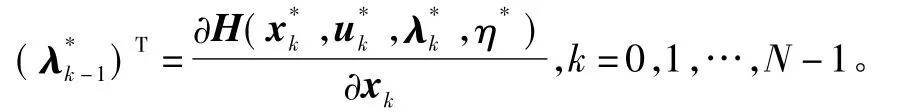
2)边界条件。
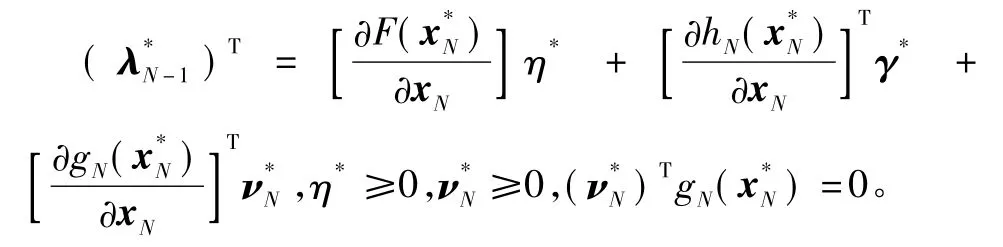
3)哈密尔顿条件。
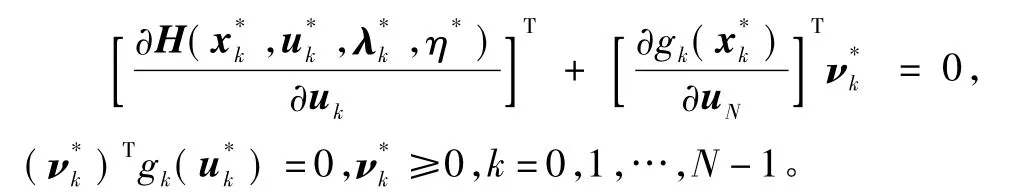
定理2是在假设条件下主要利用凸优化分离定理得到的最优性充要条件;而定理3是直接利用FJ条件得到的最优性充要条件。对比可知:定理2中所需要的拉格朗日乘子的数量大大减少了,因定理3中额外需要的存在,这简化了对最优化问题是否存在最优解的检验过程,尤为重要的是,在定理2的证明中还详细给出了拉格朗日乘子及实数 η*的取值方法,而在定理3中却未给出任何相关的取值信息。
3 仿真算例
无人机航迹规划是在综合考虑无人机到达时间、油耗、威胁规避以及可飞行区域等因素的前提下,为无人机规划出最优或者满意的飞行航迹,以保证圆满地完成飞行任务,并安全返回基地[12]。
无人机的动静态特性可通过在惯性坐标系下一离散线性状态空间模型表征,同时附加若干关于动态和惯性下的线性矩阵不等式约束条件。在无人机航迹规划问题描述中,无人机状态向量si由速度向量和位置向量构成,si=[pivi]T∈R6。其中:位置向量 pi=[xi,yi,,速度向量记无人机初始状态为,期望终端状态为s,优化时域长度为N,
f规划时域N的长度依赖于可获得的计算能力和可检测环境的距离范围。设第i步的代价函数L(si,ui)为一分段线性函数形式,ui表示输入控制矢量,即需要设计的优化变量,ui为无人机的参考速度或者加速度等可控变量。终端分段线性代价函数记为F(sN)。从而得到在N时间段内最优航迹规划问题为
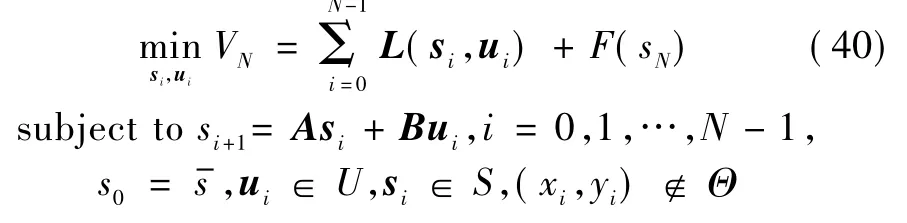
式中:(xi,yi)表示无人机的位置坐标;S表示状态变量集;U表示控制输入集;Θ表示在已知飞行范围内的障碍区域。此时只约束位置矢量中的前两个变量,这常见于二维平面中的障碍物约束,若增加位置矢量中关于zi的约束即为三维空间中的地形区域约束。
考虑二维平面中矩形障碍物的左下角顶点坐标为(xmin,ymin),右上角顶点坐标为(xmax,ymax)。因无人机要避开矩形障碍物,从而无人机的每一个轨迹点(xi,yi)都应该满足的约束条件为
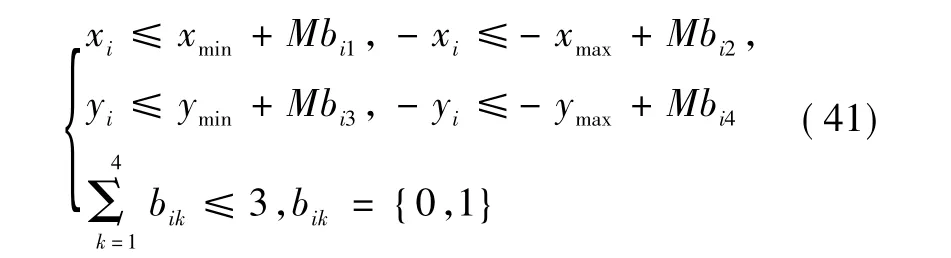
式中,M为一个较大的正数。考虑飞行时间最短和消耗燃料最少的代价函数为
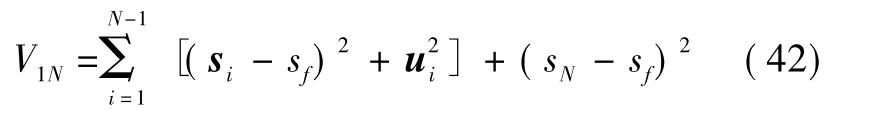
式中:第1项为每步的离散状态xi与期望的终端状态xf之间偏离代价;第2项为燃料代价;第3项为实际终端状态xN与期望终端状态xf之间的偏离代价。基于上述的简单说明,在无人机从初始点x0到目标点xf的最优航迹规划问题可归纳为如下的数学优化问题
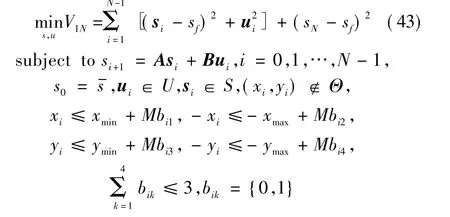
对数学优化问题式(43),利用凸优化算法来进行求解,首先需要把众多的等式约束和不等式约束进行合并。在每次优化求解得到的N-1个最优控制输入序列中仅取第1项应用于实际系统中,重复上述优化过程。仿真中取
无人机的初始状态为原点(0,0),期望的终端状态为(60,70),各个矩阵障碍物的位置如图3所示。
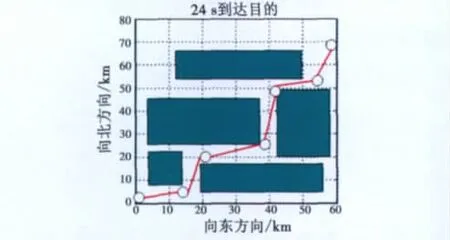
图3 无人机从原点起飞到目的的路径Fig.3 The path of the unmanned helicopters from origin to destination
采样时间Δt=1,优化时域N=6,对式(43)利用滚动时域策略进行求解,得到无人机的最优航迹路径,见图3。无人机从原点(0,0)处开始向东飞行,经过24 s的飞行时间到达终点位置(60,70)。图4表示代价函数随着时间而逐渐递减,充分说明由滚动时域控制中凸优化迭代算法得到的最优控制输入序列是优化问题的一个最优解。
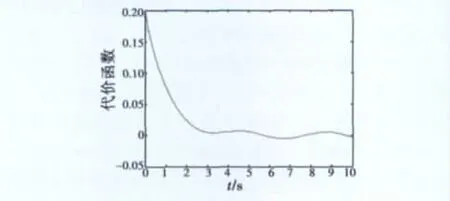
图4 代价函数随时间的递减图Fig.4 The decrease of cost function vertus time
4 结语
对于非线性系统的滚动时域控制,在无和有集合约束情况下,结合凸优化理论给出非线性系统的滚动时域控制中最优化问题存在全局最优解的充要条件,将此充要条件和传统经典的最优性条件进行比较,得出最优解存在的简化检验过程。
[1] GUARDABASSI G.Virtual reference direct method:An off-line approach to data-based control system design[J].IEEE Transactions of Automatic Control,2000,45(5):954-959.
[2] LENNART L.System identification:Theory for the user[M].Prentice Hall,1999.
[3] BAZANELLA A S.Iterative minimization of H2control performance criteria[J].Automatica,2008,44(10):2549-2559.
[4] CAMPI M C.Direct nonlinear control design:The virtual reference feedback tuning approach[J].IEEE Transactions of Automatic Control,2006,51(1):14-27.
[5] LECHINI A,CAMPI M C.Virtual reference feedback tuning for two degrees of freedom controllers[J].Internation Journal ofAdaptiveControland SignalProcessing,2002,16(10):355-371.
[6] PINTELON R,SCHOUKENS J.System identification:A frequency domainapproach[M].New York:IEEE Press,2001.
[7] BOYD S,VANDENBERGHE L.Convex optimization[M].UK:Cambridge University Press,2008.
[8] NOCEDAL J,WRIGHT S J.Numerical optimization[M].Berlin:Springer-Verlag,2002.
[9] 李向旭,张曾科,姜敏.两轴稳定平台的模糊-PID复合控制器设计与仿真[J].电光与控制,2010,17(1):69-72.
[10] 王建宏,王道波.机载稳定跟踪平台速率回路的内模H∞控制[J].电光与控制,2011,18(1):20-24.
[11] 王建宏.基于先进辨识的控制策略研究及其应用[D].南京:南京航空航天大学,2011.

