一种改进的非线性MIMO系统鲁棒自适应反推控制
孙强和, 童止戈
(空军工程大学工程学院,西安 710038)
0 引言
近年来,反推控制方法受到了国内外学者的广泛关注[1],针对非线性SISO系统反推控制的研究取得了大量成果[2-4]。对于非线性 MIMO 系统,由于各状态变量和输入信号相互耦合,使得其分析和控制复杂得多。现有文献对非线性MIMO系统的反推控制问题取得了少量研究成果[5-6],但其设计步骤仍类似SISO系统的设计过程,其每步设计都是相对标量系统进行的,不易简单推广到每个子系统都是多变量的系统设计过程中。事实上,大量的系统具有非线性和多变量特性,例如导弹、飞机等多变量非线性系统,其数学模型往往可以转化为每个子系统都是向量的不确定严反馈非线性MIMO系统。因此,研究子系统为向量形式的多变量不确定非线性系统的控制问题具有现实意义和重要性[7-8]。
另一方面,尽管文献[9]通过引入低通滤波器消除了传统反推控制固有的“微分爆炸”问题,但由于低通滤波器的引入,使得其跟踪误差不再收敛到零,而是收敛到一个较小的残集内,能否引入一种技术使跟踪误差的L∞性能指标被保证成为一个值得研究的内容。
基于以上分析,本文就一类子系统为向量形式的不确定严反馈非线性MIMO系统,提出一种改进的鲁棒自适应反推控制方法。具体方案为在反推过程中通过引入一个低通滤波器,取消控制律中的微分项;并且应用RBF神经网络在线逼近模型的不确定性;同时,在控制律设计中引入一个自适应鲁棒控制项来补偿神经网络逼近误差和未知外界干扰的影响,提高系统的鲁棒性,使整个系统获得更好的跟踪控制性能。通过适当选择设计参数及初始化误差变量,使得跟踪误差的L∞性能指标被保证。最后,基于Lyapunov稳定性定理证明闭环系统的所有信号半全局一致终结有界。所设计的控制器无需控制增益矩阵可逆的条件,控制器结构简单,可以直接应用于导弹、飞机等多变量非线性系统的控制。
1 问题描述
考虑下面一类不确定严反馈非线性MIMO系统

为系统输出。设

其中:fi0(·),gi0(·)为系统的名义值,满足fi0(0)=0;Δfi(·),Δgi(·)为存在的不确定性。
控制目标:设计控制律u,消除系统不确定性和外界干扰对系统的影响,使输出y=x1跟踪期望指令信号x1c,且具有良好的过渡过程品质。
2 改进的鲁棒自适应反推控制律设计
本文中使用RBF神经网络在线逼近未知的非线性不确定函数项。其结构简单,学习收敛速度快,能够逼近任意非线性函数。给定任意一个光滑非线性函数f:ΩZ→Rp,则存在一个 RBF 基函数向量 ξ:Rq→Rl及理想权值矩阵 W*∈Rl×p,使得

其中:ε(Z)∈Rp为神经网络的逼近误差,‖ε(Z)‖≤εM,εM为系统的设计参数。理想权值矩阵W*取为在紧集ΩZ⊂Rq内使得‖ε(Z)‖最小的W,定义为

系统Σ的不确定非线性函数向量可表示为

根据式(5),系统不确定非线性函数向量可用RBF神经网络在线逼近。

为了简化设计,下面的推导过程将 fi0(·)、gi0(·)和di(·)分别简写为 fi0、gi0和 di。为完成控制器设计需做如下假设。
假设1 gi0(·)有界,即存在常数 bMi≥bmi>0,使得 bmi≤‖gi0(·)‖≤bMi。


改进的鲁棒自适应反推控制器设计过程如下。
1)步骤1,考虑系统Σ的第1个子系统,定义误差状态向量

式中:e1=[e11,e12,…,e1m1]T,对其求导得


此时,不难选取第1个子系统的虚拟控制律和自适应律为


但是,在下述反推设计过程中,将使用x2c的微分信号,为了避免对它的解析运算,如果选择

且保证x2c能渐近收敛到,则同样可以保证e1收敛到0附近的某个邻域中。故可考虑通过低通滤波器来获得x2c和,有

式中τ2为滤波器时间常数。
2)步骤i,考虑系统Σ的第i个子系统,定义误差状态向量

式中:ei=[ei1,ei2,…,eimi]T,对其求导得

选取第i个子系统的虚拟控制律和自适应律为

步骤n:考虑系统Σ的第n个子系统,定义误差状态向量

式中,en=[en1,en2,…,enmn]T,对其求导得

选取第n个子系统的虚拟控制律和自适应律为
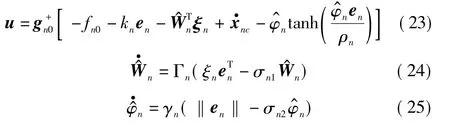
3 闭环系统稳定性分析
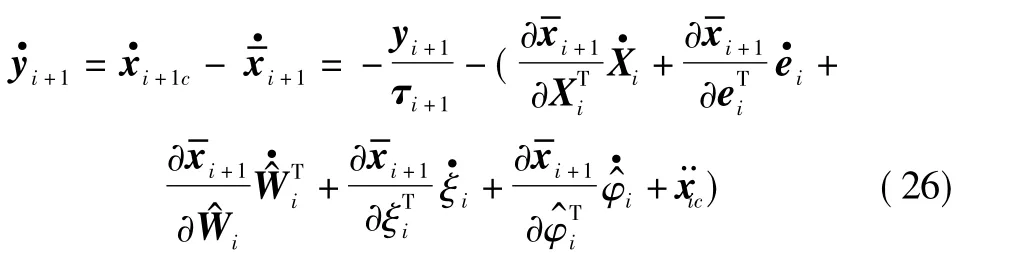
可见

故

其中:Ci+1(·)是某一连续函数。
由式(9)、式(13)、式(16)和式(17)可得ei动态值
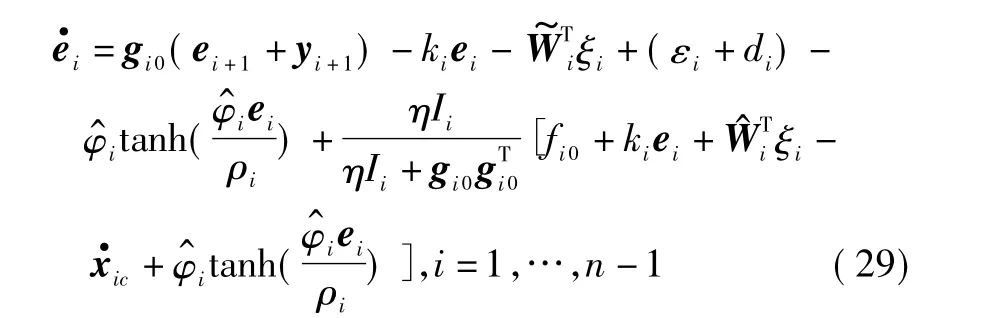
应用文献[10]中的引理可推导出
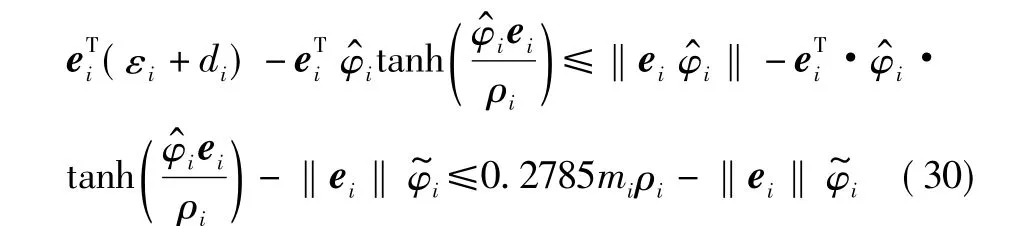
因此,

类似地,
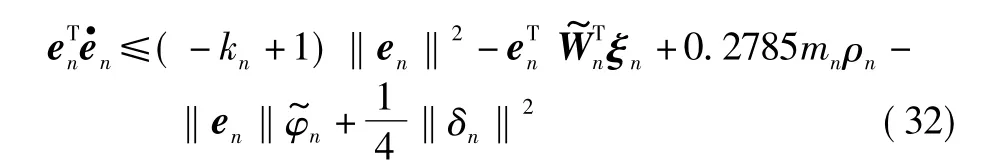

定理考虑式(1)构成的闭环系统,定义Lyapunov能量函数
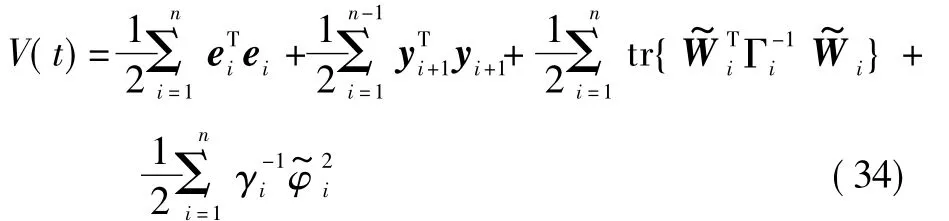
在满足假设1~假设4的条件下,控制律选择为式(23),则对于任意给定正常数p,若V(0)≤p,那么存在设计参数 ki,τi+1,ρi,σi1,σi2,Γi,γi,使闭环系统的所有信号半全局一致终结有界。通过适当选择设计参数及初始化误差变量,跟踪误差e1可收敛到原点的一个任意小邻域内,且其L∞跟踪性能被保证。
证明 V(t)对时间t的导数,并将式(11)、式(12)、式(18)、式(19)、式(24)和式(25)代入,整理得
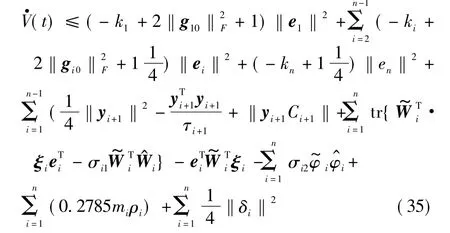
由假设2和定理表述知,对于任意K0>0和p>0,集合
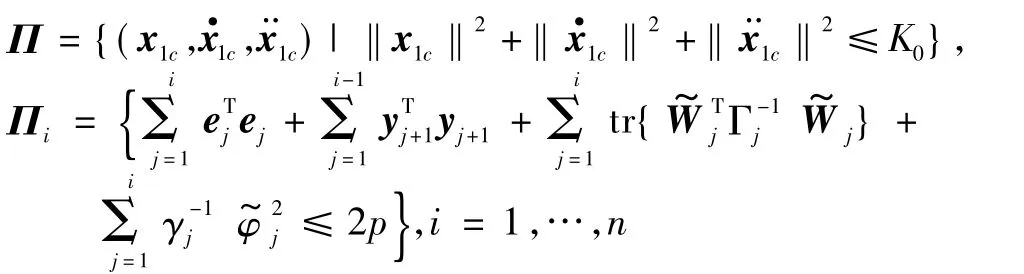
分别是R3和 R4i-1内的紧集。那么,Π×Πi也是R4i+2内的紧集。因此,‖Ci+1‖在集合Π×Πi内存在一个最大值Mi+1。利用Young’s不等式知,对于任意μ>0有



选择设计参数

则式(37)可表示为


那么,

设式(11)、式(12)、式(18)、式(19)、式(24)和式(25)中估计参数初始值为0,即1,…,n。通过设置,n,使ei(0)=0。由式(8)、式(13)、式(14)、式(15)、式(17)、式(20)、式(21)和式(34)知 ei(0)=0,i=1,…,n,

由式(38)和式(39)可得

由上式和式(41)可得
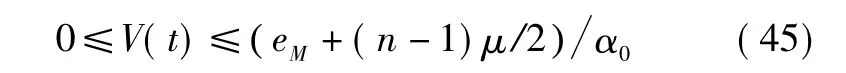
因此,
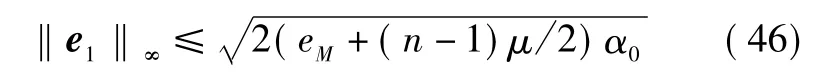
上式表明,按式(37)适当选择设计参数,使α0足够大,可使跟踪误差e1的L∞跟踪性能提高。
4 数值仿真
考虑如下非线性系统

初始状态为 x1(0)=x2(0)=[0,-0.2]T,期望信号为 x1c=[x11c,x12c]T=[0.5(sin t+sin(0.5t)),yr2=sin t]T。
按式(38)选择控制器参数k1=k2=10,Γ1=Γ2=diag[10],γ1= γ2=5,σ11= σ21=1,σ12=σ22=2,ρ1=ρ2=2,τ1= τ2=0.1。参数初始值为W^i(0)=0,φ^i(0)=0,i=1,2。神经网络隐层节点数均选为21,高斯函数中心值在区间[-1,1]内均匀间隔取值,宽度均取为1。
仿真结果如图1~图4所示。

图1 x11控制指令跟踪过程Fig.1 x11control command tracking procedure

图2 x12控制指令跟踪过程Fig.2 x12control command tracking procedure

图3 权值矩阵的L2范数Fig.3 L2norm of the NN weights:

图4 控制律曲线Fig.4 Graph of control law
图1 和图2显示输出y能很好地跟踪参考信号yr;图3和图4分别显示神经网络权值和控制信号的有界性。
5 结语
本文就一类具有模型不确定性和未知外界干扰的严反馈非线性MIMO系统,提出了一种改进的鲁棒自适应反推控制方法。该方法具有以下特点:1)通过引入低通滤波器消除了传统反推设计方法中由于对虚拟控制反复求导而导致的复杂性问题;2)自适应鲁棒控制项的引入补偿了神经网络逼近误差和未知外界干扰的影响,提高了系统的鲁棒性,使整个系统获得了更好的跟踪控制性能;3)通过适当选择设计参数及初始化误差变量,保证了跟踪误差的L∞性能指标。最后,通过Lyapunov稳定性定理证明了闭环系统的半全局稳定性,数值仿真验证了方法的有效性。
[1] 徐湘元.反推技术及其在不确定系统中的应用[J].系统工程与电子技术,2006,31(11):2703-2709.
[2] GE S S,WANG C.Direct adaptive NN control of a class of nonlinear systems[J].IEEE Trans.on Neural Networks,2002,13(1):214-221.
[3] WANG C,HILL D J,GE S S,et al.An ISS-modular approach for adaptive neural control of pure-feedback systems[J].Automatica,2006,42(5):723-731.
[4] REN B B,GE S S,SU C Y,et al.Adaptive neural control for a class of uncertain nonlinear systems in pure-feedback form with hysteresis input[J].IEEE Trans.on Systems,Man,and Cybernetics-Part B:Cybernetics,2009,39(2):431-443.
[5] GE S S,WANG C.Adaptive neural control of uncertain MIMO nonlinear systems[J].IEEE Trans.on Neural Networks,2004,15(3):674-692.
[6] 钱厚斌,张天平.控制增益符号已知的MIMO非线性时滞系统自适应控制[J].电光与控制,2009,16(8):9-14,39.
[7] 胡云安,晋玉强,张友安,等.基于神经网络的严反馈块非线性系统的鲁棒控制[J].控制与决策,2004,19(7):808-812.
[8] CHEN M,GE S S,EE HOW B V.Robust adaptive neural network control for a class of uncertain MIMO nonlinear systems with input nonlinearities[J].IEEE Trans.on neural networks,2010,21(5):796-812.
[9] SWAROOP D,HEDRICK J K,YIP P P,et al.Dynamic surface control for a class of nonlinear systems[J].IEEE Transactions on Automatic Control,2000,45(10):1893-1899.
[10] POLYCARPOU M M,IOANNOU P A.A robust adaptive nonlinear control design[J].Automatica,1996,32(3):423-427.

