雷达机动目标跟踪的卡尔曼粒子滤波算法
郑润高, 张安清
(海军大连舰艇学院信息与通信工程系,辽宁大连 116018)
0 引言
杂波环境下雷达机动目标跟踪问题主要是解决系统的非线性非高斯问题[1]。目前非线性算法主要有扩展卡尔曼滤波(EKF),不敏粒子滤波(UKF),粒子滤波(PF)。研究表明EKF、UKF只能适用非线性较弱的系统[2-3]。PF通过大量粒子表征状态概率密度的连续Monte Carlo方法,能够适应较强的非线性非高斯环境[3-4],但是稳定性不高、实时性差。文献[5 -7]的不敏粒子滤波算法(UPF)与PF相比加入了粒子状态协方差信息,需要的粒子数更少且精度比粒子滤波更高。由于需要对每个粒子状态进行采样,计算复杂性仍然较大,且在跟踪起始阶段收敛较慢。本文引入卡尔曼粒子滤波(KPF)[8-10]算法,较好地解决了精度与实时性兼容以及算法收敛性问题。
1 卡尔曼粒子滤波算法
两坐标雷达系统下,目标状态转移方程及观测方程为

其中vk-1和wk分别表示过程噪声与量测噪声。雷达量测信号zk包括目标的距离、仰角,而目标状态xk=[rxvxaxryvyay]′,系统非线性较强。
与UPF算法相似,KPF算法在PF算法的基础上,考虑每个粒子的状态及状态协方差并由此得到粒子状态估计,近似得到目标状态的先验分布,再经过粒子的重要性密度计算得到目标状态后验概率密度。对于已起始航迹的雷达机动目标KPF算法过程如下。
1)初始状态采样得到粒子为

2)粒子状态及协方差预测为

3)将极坐标下观测数据转换为直角坐标数据为

其中:r2和为距离和仰角量测噪声方差;Rd为转换得到的量测信号方差。
4)计算卡尔曼滤波增益为

5)计算粒子状态及协方差估计为


6)根据粒子状态及协方差再采样得到新的粒子为
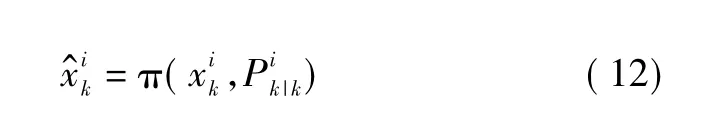
7)计算粒子似然概率、先验转移概率和推荐分布概率,得到重要性密度。
①似然概率为

②先验转移概率为

③推荐分布概率为

8)根据重要性密度重采样得到新的粒子权重集,权值归一化。
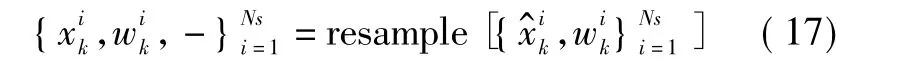
9)重复步骤2)。
相比较PF、UPF而言,KPF算法的计算量小很多,而实验表明KPF需求的粒子数很小(在接下来的仿真分析中将会给出)。图1是这3种算法的流程图比较。

图1 PF、UPF、KPF 算法流程图Fig.1 The flow chart of PF,UPF and KPF algorithms
2 仿真比较分析
模拟舰舰导弹二维空间飞行的几种方式:“俯冲机动”、“蛇形俯冲”、“转弯机动”作为实验验证数据。3种算法所使用的目标运动模型都为“当前”统计模型[11]。设定机动频率 α=1/40,加速度(单位 m/s2)上下限为[-40,40],雷达扫描周期 T=0.1 s,观测噪声方差为 Rr=diag([4020.0052]),根据式(5) ~ 式(8)得到直角坐标系下的观测噪声方差阵Rd。目标状态初始值设为X0=[x00 0 y00 0],x和y为极坐标观测值转换得到的直角坐标值。
实验中粒子数分别选择200、100、50,对算法的3种性能:最小均方误差(RMSE)、滤波时间和鲁棒性(如果发散则前两项无意义)进行10次Monte Carlo仿真。仿真环境为奔腾(R)4 CPU,2.4 GHz,512 M 内存。
2.1 仿真实验1
实验1目标俯冲机动,模拟舰舰导弹俯冲掠海飞行,总时长为91 s。18~80 s目标俯冲,迅速降低高度,其余时段直线运动。目标从开始俯冲到俯冲结束,加速度变化很快,非线性很强。这段时间有利于导弹摆脱雷达的跟踪,因此实际装备首先要考虑的是算法的实时性。由图2b可以看出两种算法在俯冲机动阶段的误差相差不大,而且起始阶段KPF算法收敛更为迅速。


图2 UPF、KPF算法跟踪俯冲机动目标性能比较Fig.2 Comparison between UPF and KPF in tracking the diving targets
2.2 仿真实验2
实验2目标蛇形机动,扫描时长370 s,13~360 s目标蛇形机动。整个阶段目标加速度变化大。因此跟踪系统的非线性非常强,对滤波器的非线性适应能力要求很高。图3a是两种算法的跟踪效果,图3b是算法的最小均方误差比。UPF捕捉目标机动所需时间较KPF算法要长30 s之多,而在稳定跟踪阶段,精度只比KPF高10%左右,KPF算法仿真时间是UPF的1/5。

图3 UPF、KPF算法跟踪蛇形机动目标性能比较Fig.3 Comparison between UPF and KPF in tracking the snaking targets
2.3 仿真实验3
实验3目标转弯运动,总时长为100 s,算法跟踪效果如图4a所示。转弯机动非线性很强。两种算法跟踪效果误差如图4b。转弯过程中,KPF算法能够迅速跟踪上目标,而UPF算法需要较长的时间才能收敛。
表1~表3列出了各跟踪参数条件下UPF、KPF跟踪“俯冲机动”、“蛇形机动”和“转弯机动”目标的性能指标。根据仿真结果得出结论:
1)UPF算法跟踪机动目标的稳定性不如KPF,目标一旦机动需要较长时间才能收敛,而KPF算法所需的时间大大少于前者;
2)UPF算法计算量是KPF的5倍左右,而精度不能高出很多;
3)KPF算法在提高运算速度(减少粒子数)的同时精度并没有下降很多。
因此跟踪非线性机动目标,KPF算法有以下优点:
1)计算复杂度小,是UPF计算量的1/5左右;
2)滤波精度相较于PF、EKPF要高,比UPF只低6%左右;
3)稳定性比UPF要好,能够快速地检测出目标的机动并跟踪上目标的航迹。
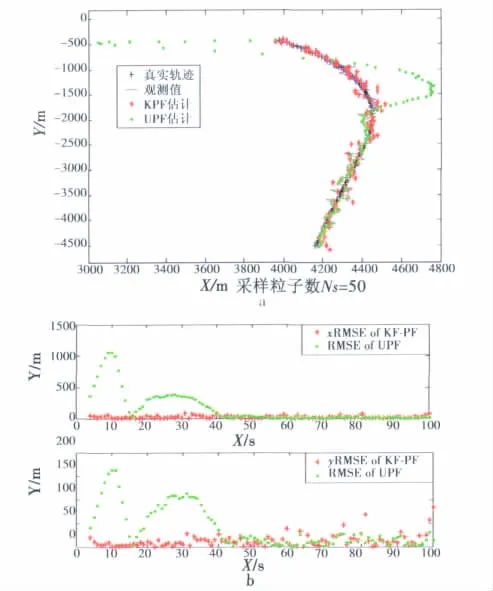
图4 UPF、KPF算法跟踪转弯机动目标性能比较Fig.4 Comparison between UPF and KPF in tracking the swerving targets

表1 俯冲机动目标跟踪效果对比(采样粒子数分别为200、100、50)Table 1 Comparison between UPF and KPF in tracking the diving targets(number of particles were 200,100 and 50)

表2 蛇形机动目标跟踪效果对比(采样粒子数分别为200、100、50)Table 2 Comparison between UPF and KPF in tracking the snaking targets(number of particles were 200,100 and 50)

表3 转弯机动目标跟踪效果对比(采样粒子数分别为200、100、50)Table 3 Comparison between UPF and KPF in tracking the swerving targets(number of particles were 200,100 and 50)
3 总结
本文基于仿真实验中发现PF算法对二维机动运动目标滤波发散,UPF算法跟踪机动目标的稳定性和实时性差的现象,引入了一种结合卡尔曼算法与粒子滤波算法的快速机动目标滤波跟踪算法,是一种计算量小、跟踪稳定性好、精度较高的混合线性/非线性滤波算法。首先通过坐标转换将极坐标观测数据转换为直角坐标数据(包括量测噪声阵的转换),然后通过卡尔曼滤波算法近似得到粒子状态的先验概率估计,然后应用粒子滤波的方法得到目标状态后验概率分布。仿真实验表明该算法具有较高非线性快速机动目标跟踪的费效比,对实现复杂电磁环境下快速机动目标的跟踪具有一定的应用价值。
[1] SHALOM Y B,DAUM F,HUANG J.The probabilistic data association filter:Estimation in the presence of measurement origin uncertainty[J].IEEE Control Systems Magazine,2009(9):82-100.
[2] ARULAMPALAM M S,MASKELL S.A tutorial on particle filters for online nonlinear/non-gaussian bayesian tracking[J].IEEE Transactions on Signal Processing,2002,50(2):174-188.
[3] DOUCET A,GODAILL S.On sequential Monte Carlo methods for Bayesian filtering[J].Statistics and Computing,2000(10):197-208.
[4] QI Cheng,BONDON P.A new unscented particle filter[C]//Acoustics Speech and Signal Processing of IEEE International Conference on ICASSP,2008:3417-3420.
[5] LANCASTER J,BLACKMAN S,YU L,et al.IMM/MHT tracking with an unscented particle filter with application to ground targets[J].Proc.of SPIE,2007,6699:19-22.
[6] PAYNE O.An unscented particle filter for GMTI tracking[C]//IEEE Aerospace Conference Proceedings,2004:1869-1875.
[7] NI Bingbing,WINKLER S,KASSIM A A.An efficient stochastic framework for 3D human motion tracking[C]//Proc.of SPIE-IS&T Electronic Imaging,2009,6805:1-10.
[8] MANDEL J,BEEZLEY J D.An ensemble kalman particle predictor-corrector filter for non-gaussian data assimilation[C]//ICCS 2009 Proceedings of the 9thInternational Conference on Computational Science,2009:470-478.
[9] LOSSE H,FRANKE U,STILLER C.Kalman particle filter for lane recognition on rural roads[C]//IEEE Intelligent Vehicles Symposium,2007:60-65.
[10] 徐剑,毕笃彦.基于卡尔曼滤波和粒子滤波级联模型的静基座惯导初始对准算法及仿真[J].电光与控制,2006,13(1):27-32.
[11] ZHOU Hongren,KUMARF K S P.A“Current”statistical model and adaptive algorithm for estimating maneuvering targets[J].AIAA Journal of Guidance,1984,7(5):596-602.

