大型运输机空投条件对落点概率偏差的影响
刘 存, 汤志荔, 张 安
(西北工业大学电子信息学院,西安 710129)
0 引言
大型运输机是现代军事快速反应、远程机动能力的关键手段。随着空投系统在抢险救灾、货物传送、兵力远程投送等方面的广泛应用,我国也开展了大型运输机的空投系统研究工作。散布是空投系统效能的重要指标之一,对空投精度有着极其重要的影响。在空投系统的精度分析中,用空投落点的概率偏差来描述空投落点的散布程度。由于各种扰动及随机因素,空投时实际落点与空投条件的对应关系和理论射表有所不同,必须对落点概率偏差进行分析与计算,才能准确地使用射表,合理地选择空投区域[1]。
引起空投落点产生偏差的主要因素有:空投条件,如空投时飞机的飞行高度、速度和姿态的误差等;空投系统的各种参数的误差等;气象条件,如随机风等。本文主要研究空投条件对空投落点概率偏差的影响。
首先,根据物伞系统运动方程,建立空投轨迹解算模型;然后,确定空投条件中各影响因素的随机分布;最后,利用蒙特卡罗方法计算仿真结果并分析空投条件对空投落点概率偏差的影响。
借助空投仿真统计试验方法,在产品研制初期,可由计算机对初步设计的产品进行仿真试验,对初步设计结果做出合理的评估;可大大减少实际空投试验的次数,节省研制人力物力,缩短研制周期。
1 空投轨迹解算模型
根据实际需要,轨迹计算模型的建立和解算基于如下的假设:1)不考虑地球转动和曲率,重力加速度恒定;2)不考虑风的影响,即物伞系统地速等于物伞系统空速;3)飞机平飞且速度恒定,俯仰角恒定;4)对于多伞系统,应用等效参数,考虑成单伞系统;5)将物伞系统视作质点。
在分析和研究空投过程的基础上,将空投过程分为4个关键阶段:1)舱内运动阶段,货台相对于货舱开始运动到货台质心离舱为止;2)自由坠落阶段,从货台质心离舱到降落伞开始充气为止;3)降落伞充气阶段,降落伞从开始充气到充满气为止;4)降落伞稳定阶段,降落伞充满气后,系统逐渐减速垂直降落至系统达到目标为止。
根据空投过程关键阶段的划分,需要建立的各个阶段的解算模型如下文所述[2-3]。
1.1 舱内运动阶段
由于货台和舱内导轨的结构对称性,货台的运动可以视为刚体的平面运动。在地面坐标系中,货台(即物伞系统)受力如图1所示。
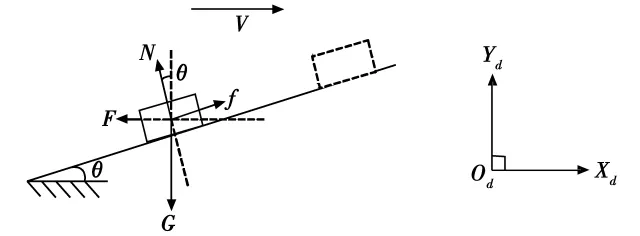
图1 舱内运动阶段受力示意图Fig.1 The force analysis of the cabin movement stage
图中:F为牵引伞拉力(N);N为物伞系统所受地板支持力(N);f为摩擦力(N);G为物伞系统所受重力(N);θ为载机俯仰角(°);V为载机空速(m/s)。
根据牛顿定律方程,最终得到化简的舱内运动模型为

式中:xd和yd分别为物伞系统位置的Xd轴和Yd轴分量(m);wx和wy分别为物伞系统速度的Xd轴和Yd轴分量(m/s);g为重力加速度(m/s2);μ为货台与舱板之间摩擦系数;θ为载机俯仰角(°);Ks为牵引伞牵引比。
1.2 自由坠落阶段
降落伞没有打开,忽略气动阻力的作用。在地面坐标系中,对物伞系统进行受力分析,如图2所示。

图2 自由坠落阶段受力示意图Fig.2 The force analysis of the free fall stage
根据假设,最终得到自由坠落阶段的运动方程为
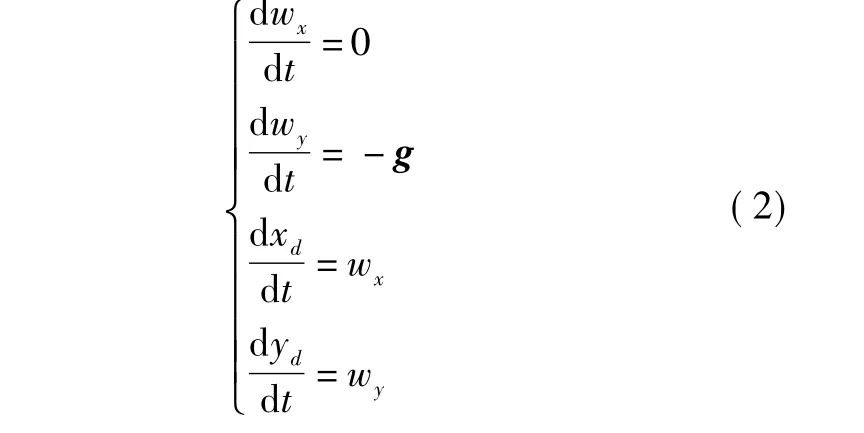
1.3 降落伞充气阶段
目前对于充气阶段的轨迹和开伞动载的计算,均属于半经验半理论的方法,还不完善和成熟。本文应用最常用的充气距离法。根据假设条件得到充气距离S为自变量的运动方程[2]为

其中所有参数的变化规律为

式中:kf为附加质量系数;S1为初始充气阶段物伞系统经过的距离;Sm为充气距离;C1为初始充气时期末的伞衣阻力特征;Cs为充满伞衣阻力特征。其他参数参考文献[2]。
1.4 降落伞稳定阶段
所谓稳定阶段是指:在伞衣充满后,气动阻力使物伞系统继续减速直至物伞系统稳定下降到着陆为止。在伞衣充满后,物伞系统的外形和质量的改变都可以忽略。因此,采用充气距离法来计算时,只要将C(C=Cs,dC/dt=0)看作常量,再用同样的方法一直计算下去,直到物伞系统运动速度不变为止(到达极限速度v=vd)。此外,注意到当速度接近极限速度时系统的减速较慢,使得稳定下降的时间很长,在实际的使用中没有必要,因此一般计算到v=1.01vd即可视为稳定阶段结束。关于物伞系统达到稳定下降速度vd之后的下降轨迹计算,只要将上述计算条件中的附加质量视为0(mf=0)即可。再计算下去,直到着陆为止。
2 空投落点概率偏差计算模型
蒙特卡罗方法(Monte Carlo Method)是一种与一般数值计算方法有本质区别的计算方法,属于实验数学的一个分支,其思想是当所求解问题是某种随机事件出现的概率,或者是某个随机变量的期望值时,通过某种实验的方法,以这种事件出现的频率估计这一随机事件的概率,或者得到这个随机变量的某些数字特征,并将其作为问题的解。它利用伪随机数模拟模型的输入参数进行统计试验,以求得输出的统计特征值(如数学期望、概率等)作为待解问题的数值解。随着现代计算机技术的飞速发展,蒙特卡罗方法已经在科学研究的各个领域中发挥重要作用,并且越来越广泛地应用于物理工程和数学工程。
应用蒙特卡罗方法解决实际问题的步骤[4]:1)根据问题的随机过程的概率统计特点,建立随机过程的概率模型;2)根据问题的特点和计算需要,采用直接模拟法,或者降低方差的方法,以提高计算效率;3)建立产生随机数的方法,建立随机抽样方法,产生随机事件、随机变量、随机函数和随机流的抽样值;4)计算问题所求解的统计近似值及其方差;5)编制计算机程序,输入数据,进行模拟计算。其仿真流程如图3所示。
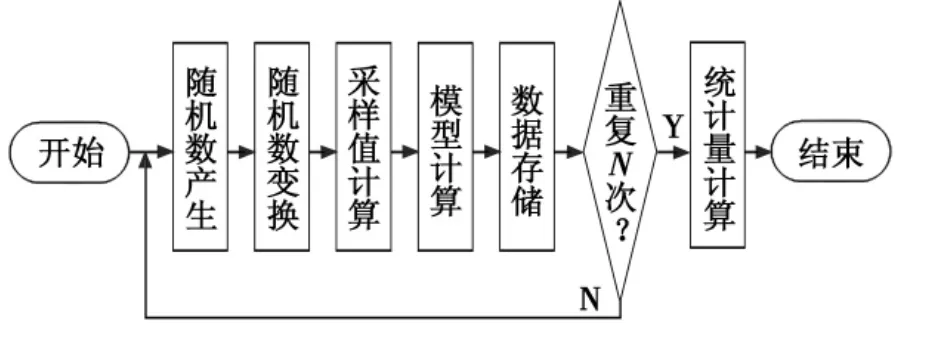
图3 蒙特卡罗方法的仿真流程图Fig.3 The simulation flow chart of Monte Carlo method
空投落点概率偏差仿真计算的理论基础是蒙特卡罗方法。利用随机值输入标准轨迹解算模型进行求解。得到的每一条空投轨迹的仿真计算结果就相当于一次实际空投试验结果。这样的试验可反复进行多次,根据数理统计的精度要求,适当选择计算的次数N,分析空投轨迹落点散布时,N 可取100 ~1000[1]。
概率偏差E是研究散布时常用术语[5]。
设随机变量X是空投系统在散布平面上落点的X坐标,其数学期望是μX,方差是若存在一个 EX>0,并使得

成立,则称EX是X的概率偏差。
根据标准正态分布规律,可以求得概率偏差EX与均方根偏差(即标准偏差)σX的关系为

EX是X的概率偏差,它不仅表示落点的散布程度,而且表示在X坐标方向上半数落点的着陆范围。
在空投轨迹计算的假设条件下,空投轨迹是一条平面曲线,位于铅垂平面之内。定义轨迹纵向为X轴,则最终得到的散布结果是空投轨迹落点在X轴上的概率偏差。
3 仿真结果及分析
本文以3种空投条件(空投高度、空投速度和俯仰角)的变化为例,分析空投条件对空投落点概率偏差的影响规律。
空投高度、空投速度和俯仰角都是在一定的取值范围内服从正态分布的随机变量。在它们的取值范围中,产生正态随机数[6],用于仿真计算,以确定随着各个因素的单调增加,落点概率偏差的变化规律。
以牵引空投为示例,对空投轨迹落点概率偏差进行计算,各种参数在通用的参数范围内选取[2],空投条件的固定参数见表1,空投条件的变化参数见表2。
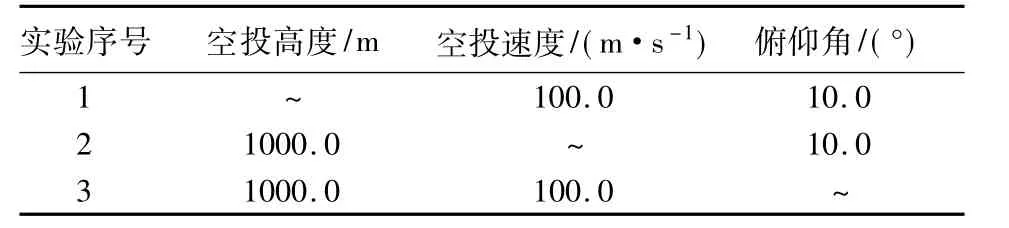
表1 空投条件固定参数Table 1 Fixed parameters of airdrop conditions

表2 空投条件变化参数Table 2 Variable parameters of airdrop conditions
不考虑误差,用空投条件参数:空投高度(1000.0 m)、空投速度(100.0 m/s)和俯仰角(10.0°)代入模型解算得到的空投轨迹如图4所示。图中横轴是落点X轴坐标,纵轴是高度。

图4 理论空投轨迹曲线Fig.4 The path curve of theoretical airdrop
应用蒙特卡罗方法(N=300),对每一种影响因素范围内的各个取值分别进行仿真计算,得到相应的概率偏差。
图5~图7分别显示了随着空投高度、空投速度和俯仰角发生变化,落点概率偏差的仿真实验的结果。图中横轴分别是空投高度、空投速度和俯仰角,纵轴是落点概率偏差EX。
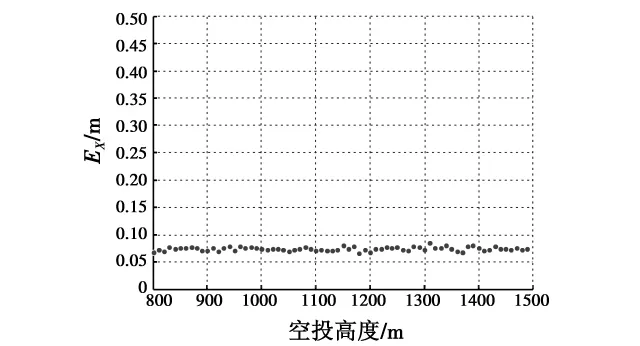
图5 空投高度影响Fig.5 Airdrop altitude influence
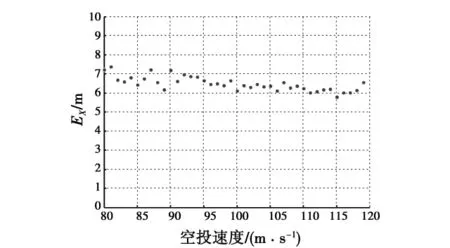
图6 空投速度影响Fig.6 Airdrop velocity influence

图7 载机俯仰角影响Fig.7 Airdrop pitch influence
由图可见,空投高度和空投速度的增加对落点概率偏差几乎没有影响,随着载机俯仰角的增加,落点概率偏差以固定比例逐渐变小。从落点概率偏差的大小来看,高度偏差的影响小于俯仰角偏差的影响,俯仰角偏差的影响小于速度偏差的影响。因此,在估计落点散布时可以忽略高度偏差,速度偏差的影响必须认真考虑,俯仰角偏差的影响可以根据精度分析要求决定是否考虑。
4 结论
本文对空投落点概率偏差的重要影响因素——空投条件进行了仿真计算;给出了确定3个主要空投条件因素分别对空投落点概率偏差影响的方法。程序计算结果说明,建立的随机空投轨迹解算模型满足对落点概率偏差解算的要求。
但是,由于影响空投落点概率偏差的因素还应包括空投系统的参数误差、气象条件,特别是风的影响等,所以进一步的研究需要考虑这两类影响因素,建立更完整的随机空投轨迹解算模型,用来确定空投落点概率偏差。
[1] 田应元,侯小波,张翠兰.投弹条件对空投弹道落点散布影响[J].水雷战与舰船防护,2009,17(1):49-52.
[2] 王利荣.降落伞理论与应用[M].北京:宇航出版社,1997.
[3] 柯鹏,杨春信,杨雪松,等.重型货物空投系统过程仿真及特性分析[J].航空学报,2006,27(5):856-860.
[4] 郭锐,刘荣忠.导弹末敏弹抛撒弹道随机模型与仿真[J].弹箭与制导学报,2006,26(2):1190-1192.
[5] 张安.航空武器系统分析导论[M].西安:西北工业大学出版社,2001.
[6] 孟晓玲,郭陈江.直升机武器系统作战精度研究及仿真[J].电光与控制,2005,12(2):48-50.

