突破思维定势 提高解题能力

蔡 伟，马贵胜

（临沂市临沭县第一初级中学，山东 临沂 276717）

思维定势是心理学的一个概念，它指的是人的一种思维惯性，即人们长期形成的一种习惯思维方向。人一旦采用某种思维方式获得成功之后，就会形成一个定势，碰到新问题，也要用老经验去试一试，按固定的模式去验证，这就是我们常说的思维定势。

一、思维定势对学生的综合解题能力的影响

思维定势对学生的综合解题能力有重要的影响。在数学教学过程中，利用这一规律，有助于学生运用所学知识和积累的经验来解题，有时能举一反三，触类旁通；但有时也会产生消极影响，妨碍思路的打开，甚至产生思维惰性。我们来看两个实验：

[实验1] 例1：求证：（1）边长为a的正三角形内任意一点到各边的距离之和是定值；

（2）边长为a的正n边形内任意一点到各边的距离之和是定值。

实验对象：初三甲组20人，乙组20人，丙组20人.

实验方法：甲组直接证（2）；乙组先证（1）再证（2），教师不作提示；丙组先由教师分析（1），然后指出（1）与（2）的异同，学生再做题。

实验结果：甲组正确率仅20%；乙组（2）的正确率达50%，另有28%的会（1）而不会做（2）；丙组的正确率高达86%。

这一实验表明：甲、乙、丙三组学生的正确率逐渐升高，说明解（1）所产生的思维定势（解题所用到的知识和思维方法）对（2）有了积极的影响;特别是丙组，在教师注重对学生的思维定势积极作用加以正确指导的情况下，思维定势所产生的正迁移的效果更加明显。

求k的值。

实验对象 初三学生50名。

这一实验表明：思维定势是造成部分学生盲目套用某种解题方法的主要原因，属于典型的负迁移。

以上两个实验表明：思维定势对学生的综合解题能力有重要的影响。在数学教学中，教师的关键是怎样积极使之产生正迁移，又要注意克服思维定势所产生的负迁移。

二、思维定势的积极影响及其正向诱导

教学过程中，教师要注重通过对知识和技能的联系、对比、类比、转化，为学生发挥思维定势的积极作用创设情景，引导学生把握课题内容和实质，找到与之相适应的知识联系，习惯用自己已经掌握的知识和技能，解释同类现象，并确定解题策略。

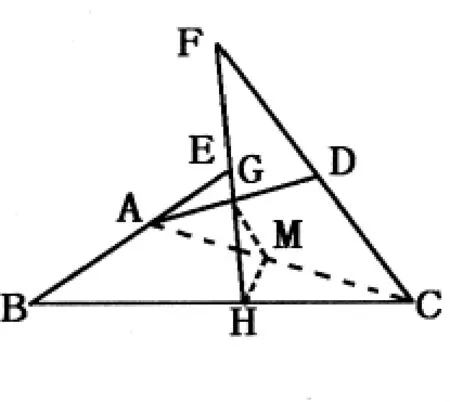
例3：如图，AB=CD，G、H 分别是AD、BC 的中点。求证：∠BEH=∠CFH

思维定势诱导1：证两角相等常用的方法——全等三角形、等腰三角形、平行线…

诱导结果：利用等腰三角形证明.这为本题确立了关键的解题方向。

思维定势诱导2：使两角转换到同一个三角形中的方法——平移、旋转、对称……

诱导结果：采用平移。

思维定势诱导3：角平移的常用方法——中位线、平行线、平行四边形……

诱导结果：连结AC，添中位线GM、HM，这就把已知和未知条件连接起来了。

教师在设疑、启发、诱导的过程中，既要排除不合题意的思路，同时启发用不同思路得出不同解法.通过正确诱导学生的思维定势，发挥其积极影响作用，使学生在思考或处理同类或相似问题时，不走或少走弯路，做到举一反三，触类旁通，提高思考效率和综合解题能力。

三、思维定势的消极影响和突破方法

思维定势在思考有创新性的问题时，往往起到阻碍作用，因此，突破思维定势就是要善于主动摆脱原来的思维模式，将思路指向新的领域或新的客体“.空城计”是大家熟知的一个三国故事：身经百战的司马懿深知“兵不厌诈”，结果担心诸葛亮的空城里有“诈”，疑心空城内部有十面埋伏，在150000比2500军士的优势下而不敢进城。是思维定势使司马懿中了“空城计”，而诸葛亮的“空城计”的设计则是典型的突破思维定势的好例子。

在数学教学过程中，怎样突破思维定势，消除其在解题中的消极影响呢？

（一）强化概念教学，突破思维定势

正确的思维来源于正确的概念，而学生常因概念模糊而产生错解.例如常有学生在解x2-16＞0时，错解为：移项 x2＞16，两边同时开平方得 x＞±4。这是受解方程概念的定势的影响；解＞0时，错解为：去分母得x＞0，这是受整式不等式的影响。因此应通过概念的应用让学生深化理解概念，避免因某种思维定势误入歧途。

（二）重视特例教学，突破思维定势

根据中学生心理特点，他们对于某一新知识和方法，开始苦于掌握不了，而一旦用熟了后又会形成思维惯性，甚至有时乱用。

因此，可以通过做一些初看起来似乎适用于某一公式或方法，但仔细分析又行不通的特例（如本例），让学生体会某一公式或方法的局限性，以便今后解题用同样的方法时能突破思维定势，从而采取灵活的解题策略。

（三）注重综合能力培养，突破思维定势

在正确的熟记概念法则的基础的同时，注重综合能力的培养，是突破思维定势的关键。

1.培养学生的审题能力

针对部分学生对貌似相同的问题不认真审题，不能正确分析题设与结论的差异，教师在教学每一道例、习题时，要引导学生认真审题，挖掘题设和结论中所有条件及相互联系，以便正确解题。

2.培养学生的发散思维能力

数学教学过程中，要注意引导学生广开思路，一题多解。针对思维定势影响解题的灵活性，那么培养思维的灵活性，可防止思维定势的负迁移。实践证明，一题多解是活跃学生思维的好方法。

3.培养学生的逆向思维能力

《司马光砸缸》是大家熟悉的故事：在一个小朋友不小心掉进一个盛水的大缸中时，在场的小朋友想的是“人离开水”的救人方法，可因为水缸又高又大，而无法实现；司马光却顺着相反的作用过程思考，即想法是“水离开人”，于是有了“砸缸放水”的方法，救出了伙伴。逆向思维使司马光获得了成功，这个故事至今仍为人们津津乐道。有时按常规思路解题困难较大时，若采用逆向思维，则能有效的突破思维定势。

习惯思维 用加减消元法先求出未知数x，进而求y。

显然2002、2003是二次方程m2-xm+2000y=0的两个根，∴2002+2003=x，2002×2003=2000y。

∴x=4005，y=2005.003。

综上所述，教学过程中，我们既要正确诱导学生的思维定势，促进思维渐进性向突变性发展，又要适时突破思维定势，激发学生的创新思维，从而打开新思路，发现新思想、新方法，这对于提高学生的数学思维素质和综合解题能力都有重要的意义。