说解题——一种别开生面的说课
刁成海
(徐州市沛县教育局教育科学研究所,江苏 徐州 221600)
说课,是近几年来教学研究、教师教学能力测试和教师基本功训练的一种常见的活动形式,在教师招聘、职称晋升、优质课评比、教师基本功大赛等工作中,大量地采用了这种活动形式。这种说课形式,之所以越来越受到各级各类教育行政部门和教育教学研究部门的青睐,是因为它不仅实施起来省时省力容易操作,而且能够在一定程度上反映老师的专业知识水平、教育教学理论素养,也能反映老师的实践能力的综合水平。
一道试题的说课是说课的一种特殊形式。下面以2道试题为例,来谈谈这种说课的一般程序。
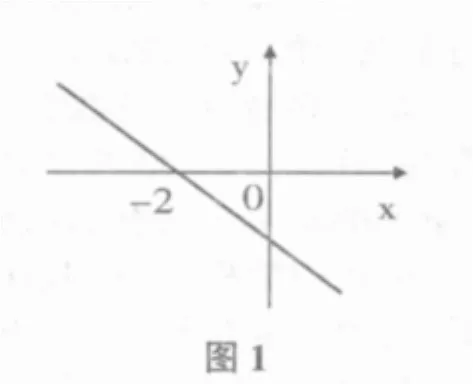
试题1 (2010年.江苏泰州)一次函数y=kx+b(k为常数且k≠0)的图象如图1所示,则使y>0成立的的取值范围为_______.y
试题2 (2011江苏无锡)如图2,在▱ABCD中,E、F为对角线BD上的两点,且∠BAE=∠DCF.
求证:BE=DF.
一说试题命制背景。这道试题是在学生学习了哪些知识后用的。试题1是一道中考题,可以放在学完一次函数后让学生练习。试题2也是一道中考题,它可以放在学完平行四边形后让学生练习。
二说试题考查目的。这道试题想考查学生哪些方面的知识点和数学思想方法。试题1主要考查学生能否把二元一次方程、一次函数和一元一次不等式联系起来,考查对一次函数图像的识图能力和数形结合的数学思想方法。试题2主要考查平行四边形、全等三角形的知识以及化归的数学思想方法。

三说试题讲评方法(教学设计)。这道试题的教学方式以及学生的学习方式我是怎样设计的。这一环节应该是说课的重点,也是反映一个教师教学理念的关键步骤。在讲评这一环节,我的做法是:先出示试题,让学生读题、画图、审题、分析,进行独立思考、各自练习;然后小组交流讨论,交流讨论后,由3个小组各出一位代表展示学习成果,并请其他同学进行评析。在这一过程中,教师是学生学习的组织者、引导者、合作者,该由学生思考的,让学生思考,该由学生回答的,老师绝不包办代替,不多说半句。该环节完成后,教师点拨。
四说试题的解题的思路分析。这一环节重点反映老师的专业素养和分析问题、解决问题的能力。试题1.你是怎样想到这种方法的呢?观察图像可知,直线在x轴上方即y>0时,x的取值在-2的左侧,故填x<-2.试题2.欲证BE=DF,只须证△ABE≌△CDF,下面寻找△ABE≌△CDF的条件,∵▱ABCD 中,AB=CD,AB∥CD,∴∠ABE=∠CDF,又 ∵∠BAE=∠DCF,∴△ABE≌△CDF,∴BE=DF.
五说试题的一题多解和变式引申。这一环节既能考查老师的发散性思维能力,还能考查老师的灵活性,也能考查老师对前后知识体系的把握,更能看出老师的专业功底。
试题1可作如下引申:
①一次函数y=kx+b(k为常数且k≠0)的图象如图所示(同上图),则使y<0成立的x的取值范围为_____.
②一次函数y=kx+b(k为常数且k≠0)的图象如图所示(同上图),则下列说法:①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=-2.其中说法正确的有______(把你认为说法正确的序号都填上).
③变式(2010年.湖北武汉)如图,直线y1=kx+b过点 A(0,2),且与直线 y2=mx 交于点 P(1,m),则不等式组mx>kx+b>mx-2的解集是 _______.
试题2可作以下引申和变式:

1.(2011浙江义乌)如图,已知E、F是▱ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.
(1)求证:△ABE≌△CDF;
(2)请写出图中除△ABE≌△CDF外其余两对全等三角形(不再添加辅助线).
2.(2011四川凉山州)如图,E、F是▱ABCD的对角线AC上的点,CE=AF,请你猜想:线段BE与线段DF有怎样的关系?并对你的猜想加以证明。


3.(2010年江苏宿迁)如图,在▱ABCD中,点E、F是对角线AC上两点,且AE=CF.求证:∠EBF=∠FDE.

(第3题图)
六说试题小结或解题后的反思。这一环节常常被老师所忽视。一道试题千辛万苦解出来之后,应该引导学生认真地进行解题后的小结或反思:试题的意图是什么?要考查的知识点和能力以及数学思想是什么?这道试题牵扯到哪些知识与数学思想方法?你是怎样想到这种解法的?解题的基本步骤有哪几步?有没有一题多解或多题一解?还可以怎样引申?我在解这道试题时漏掉了什么?哪些方面没有想到?解这类问题有没有规律可循?在今后我再解这类试题时应该注意哪些问题等等。试题1解题后的反思:二元一次方程转化为用含一个未知数的代数式表示另一个未知数,即一次函数.在直角坐标系中划出其图像即可直观地看出当自变量取何值时,函数值y的值是大于0、等于0、还是小于0,这也是数形结合思想方法的简单运用.试题2解题后的反思:平行四边形和全等三角形关系非常密切,要解决平行四边形的有关问题,常常转化为三角形的问题。但是,凡是可以用平行四边形知识证明的问题,不要再回到三角形全等证明,应直接运用平行四边形的性质和判定去解决问题。
这种说课形式,笔者感到耳目一新。虽然只是说一道试题的说课,但是同样也能很好地反映一个老师的教学能力水平。这种形式的说课,和说一节完整的课的说课形式具有同样的功效,甚至比说一节完整的课更灵活,更精练,更便于操作,更能测出教师的综合素养和综合能力,大家不妨一试。

