初中因式分解的拓展与研究

☉江苏苏州市郑华学校 吕亚军

初中因式分解的拓展与研究

☉江苏苏州市郑华学校 吕亚军

一、问题的提出

因式分解是代数式的一种重要的恒等变形，它与整式乘法是相反方向的变形，在分式运算、解方程及各种恒等变形中起着重要的作用.在高中数学中，我们除了会初中课本涉及的提取公因式法和公式法（平方差公式和完全平方公式）外，还有公式法（立方和、立方差公式）、十字相乘法和分组分解法等，但是这点内容在高中教材和初中教材中都没有讲解，本文给予补充.

二、公式法（立方和与立方差公式）

在第一讲里，我们已经学习了乘法公式中的立方和、立方差公式：

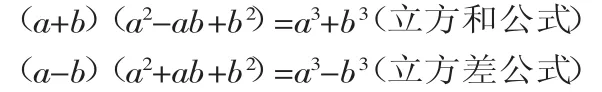
因为因式分解与整式乘法正好是互为逆变形，所以把整式乘法公式反过来写，就得到：

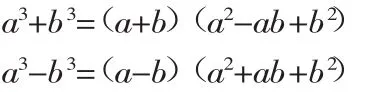
这就是说，两个数的立方和（差），等于这两个数的和（差）乘以它们的平方和与它们积的差（和）.

运用这两个公式，可以把形式是立方和或立方差的多项式进行因式分解.

例1 用立方和或立方差公式分解下列各多项式：

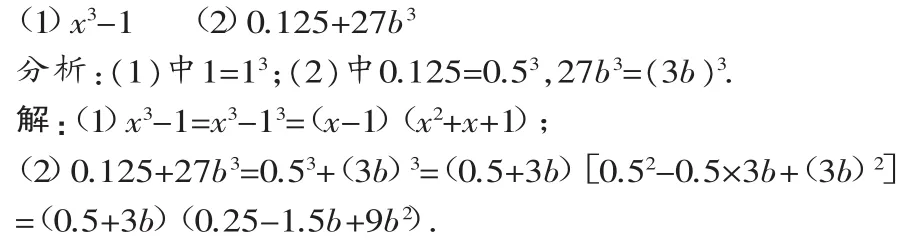
点评：（1）在运用立方和（差）公式分解因式时，经常要逆用幂的运算法则，如8a3b3=（2ab）3，这里逆用了法则（ab）n=anbn；（2）在运用立方和（差）公式分解因式时，一定要看准因式中各项的符号.

例2 分解因式：

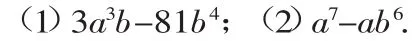
分析：（1）中应先提取公因式再进一步分解；（2）中提取公因式后，括号内出现a6-b6，可看成是（a3）2-（b3）2或（a2）3-（b2）3.

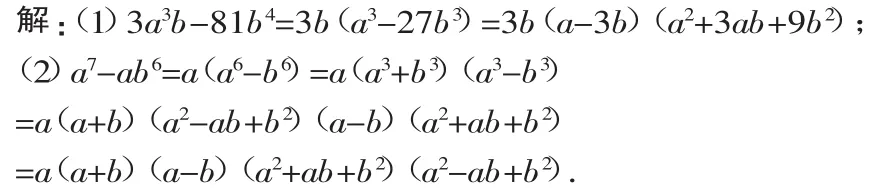
三、十字相乘法

1.x2+（p+q）x+pq型的因式分解

这类式子在许多问题中经常出现，其特点是：（1）二次项系数是1；（2）常数项是两个数之积；（3）一次项系数是常数项的两个因数之和.

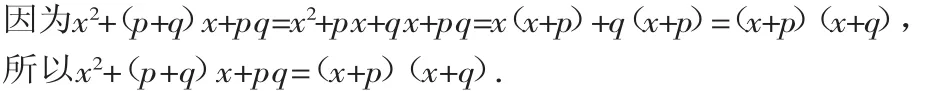
运用这个公式，可以把某些二次项系数为1的二次三项式分解因式.

例3 把下列各式因式分解：

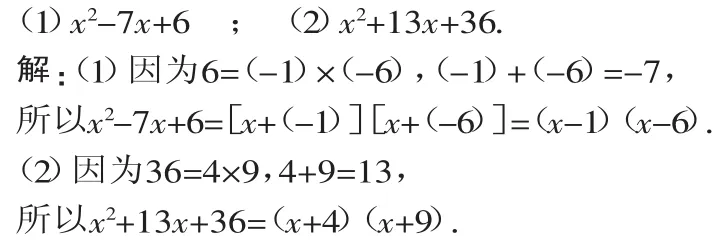
点评：由此例可以看出，常数项为正数时，应分解为两个同号因数，它们的符号与一次项系数的符号相同.

例4 把下列各式因式分解：

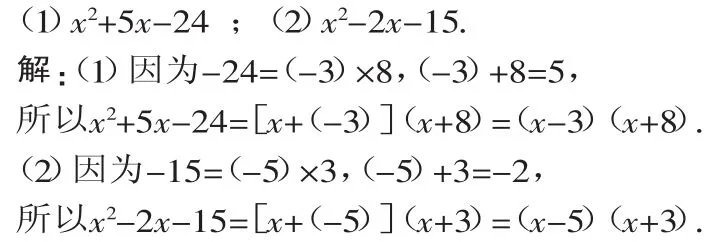
点评：由此例可以看出，常数项为负数时，应分解为两个异号因数，其中绝对值较大的因数与一次项系数的符号相同.

例5 把下列各式因式分解：

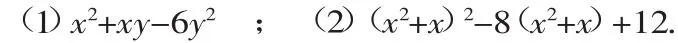
分析：（1）把x2+xy-6y2看成x的二次三项式，这时常数项是-6y2，一次项系数是y，把-6y2分解成3y与-2y的积，而3y+（-2y）=y，正好是一次项系数.

（2）由换元思想，只要把x2+x整体看成一个字母a，可不必写出，只当是分解二次三项式a2-8a+12.

这种借助画十字交叉线分解系数，从而将二次三项式分解因式的方法，叫做十字相乘法.

必须注意的是分解因数及十字相乘都有多种可能情况，所以往往要经过多次尝试，才能确定一个二次三项式能否用十字相乘法分解.

例6 把下列各式因式分解：

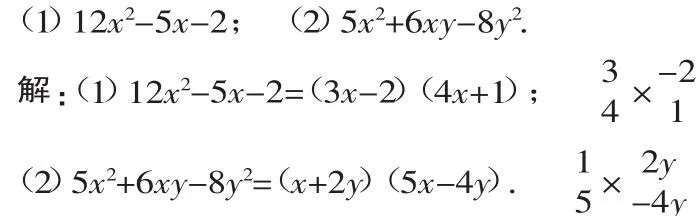
点评：用十字相乘法分解二次三项式很重要.当二次项系数不是1时较困难，具体分解时，为提高速度，可先对有关常数分解，交叉相乘后，若原常数为负数，用减法“凑”，看是否符合一次项系数，否则用加法“凑”，先”凑”绝对值，然后调整，添加正、负号.

一般地，把一个多项式因式分解，可以按照下列步骤进行：

（1）如果多项式各项有公因式，那么先提取公因式；

（2）如果各项没有公因式，那么可以尝试运用公式来分解；

（3）如果用上述方法不能分解，那么可以尝试用分组或其他方法（如十字相乘法）来分解；

（4）分解因式，必须进行到每一个多项式因式都不能再分解为止.