平面代数曲线的PH-C曲线逼近

寿华好，江 瑜，缪永伟

（1.浙江工业大学 理学院，浙江 杭州 310023；2.浙江工业大学 计算机科学与技术学院，浙江 杭州 310023）

平面代数曲线的PH-C曲线逼近

寿华好1，江 瑜1，缪永伟2

（1.浙江工业大学 理学院，浙江 杭州 310023；2.浙江工业大学 计算机科学与技术学院，浙江 杭州 310023）

代数曲线的近似参数化问题是计算机辅助几何设计与图形学领域的一个重要问题.由于PHC曲线综合了Bézier曲线，PH曲线以及C曲线的许多优良性质，从而用PH-C曲线逼近代数曲线就显得十分必要.首先根据曲线的凹凸区间和单调区间对代数曲线进行合理分割，然后根据曲线段两端点的切线确定曲线段的三角形凸包，进一步根据此三角形凸包确定3次PH-C曲线的控制多边形，这样得到的PH-C逼近曲线保持了原代数曲线的一些重要几何性质，如单调性、凹凸性和G1连续性，并且通过算法的递归调用，可以将逼近误差控制在给定的范围之内.数值实验表明，该算法提供了平面代数曲线近似参数化的一条有效途径.

代数曲线；PH-C曲线；曲线逼近

PH曲线由于其各坐标分量导数的平方和恰好为一个完全平方式，从而与一般的参数多项式曲线或代数曲线相比有重要的计算优势，例如：PH曲线具有精确的弧长表示，作为数控路径的PH曲线之等距线是有理曲线.对于离散数据的插值，PH曲线往往比普通参数多项式曲线具有相对均匀的曲率分布，从而有更光顺的轨迹，并且能精确计算其弯曲能量等等.因此，PH曲线在CAD／CAM等相关领域得到了广泛的应用.许多学者已经对PH曲线进行了大量深入的研究：历史上Farouki等首先给出了平面多项式曲线是PH曲线的充要条件及PH曲线的几何构造［1］，之后，Farouki等［2］分别独立地得到了类似的空间多项式曲线是PH曲线的条件.Dietz［3］得到的空间多项式曲线是PH曲线的条件与Farouki和Sakkalis得到的平面多项式曲线是PH曲线的条件具有类似的结构，只不过前者更复杂.事实上，文献［2］可以看作是文献［3］的特殊情况.在此基础上，许多关于PH曲线的研究工作得以展开，如用三次PH曲线构造平面Bézier曲线的等距线算法［4］.

C-曲线是定义在空间L＝span｛sint，cos t，1，t，t2，…，tn－3｝中的曲线.它最早是由张纪文［5－7］提出，与多项式曲线相比，C-曲线可以精确地表示圆、椭圆、摆线等，并且求导方便，具有许多与Bézier曲线类似的性质，如对称性、几何不变性和保凸性等.此外，C-曲线还是一类形状可调的曲线，即在控制多边形不变的情况下，C-曲线的形状还可以通过它内在的一个参数调节.因此C-曲线得到了越来越广泛的运用，如 Morin等［8］提出了CB-样条的细分算法，并用它来构造旋转曲面.

由于PH-C曲线［9］同时具有PH曲线和C曲线的诸多优良性质，从而用PH-C曲线去逼近代数曲线就显得非常必要.笔者给出了代数曲线的PH-C曲线逼近算法：代数曲线分段时同时考虑了拐点、极值点和奇点，使得逼近曲线保持原始曲线的凹凸性的同时保持单调性和G1连续性.并且逼近曲线具有PH曲线和C-曲线的诸多优点.递归调用逼近算法，可以将误差控制在指定的范围之内.

1 PH-C曲线

1.1 C-曲线

由于高阶PH-C曲线只可能是直线或者是多项式曲线［9］，因此笔者只从四阶三次PH-C曲线着手.给定平面上四个控制顶点pi＝（xi，yi），i＝0，1，2，3，四阶C-Bézie曲线定义为

四阶C-曲线具有一般形式，即

其中：vi＝（vix，viy），i＝0，1，2，3是控制顶点pi的线性组合.将式（1）所表示的C-Bézier曲线换成它的一般形式（2），可以得到vi与控制点pi，i＝0，1，2，3的关系为

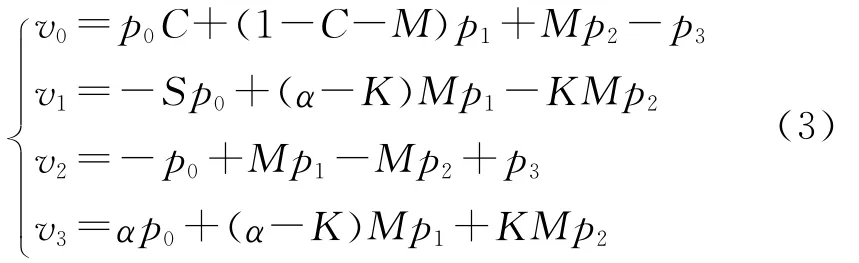
1.2 PH-C曲线

定义1 对于平面C-曲线P（t）＝（x（t），y（t））∈Γn，若存在z（t）∈Γn－1，使得曲线导数P′（t）＝（x′（t），y′（t））满足x′（t）2＋y′（t）2＝z（t）2，则称该曲线是PH-C曲线［9］.

2 代数曲线段的三角形凸包

2.1 代数曲线的分段

对于已知代数曲线，首先根据文献［10］将其进行分段，使得代数曲线在每个分段区间上具有固定的凹凸性和单调性，然后计算每段代数曲线两端点处的切线［11］.

2.2 曲线段的三角形凸包

假定分割后的某条代数曲线段为A∶F（x，y）＝0，x∈［a，b］，设它的两个端点为p0，p3，曲线段在这两个端点处的切线记为T0，T3，不妨设，T0，T3必相交于一点，记交点为O.这样p0，O，p3形成了曲线段的三角形凸包（见图1）.

图1 曲线段A的三角形凸包Fig.1 The convex hull of curve segment A

3 代数曲线的PH-C曲线逼近

3.1 控制多边形的确定

由于C曲线具有旋转、平移、伸缩不变性，不妨采用文献［9］的做法以Δp0Op3的顶点O为原点，Op0为x轴所在直线，且p0＝（1，0）（如图2），则控制顶点坐标为

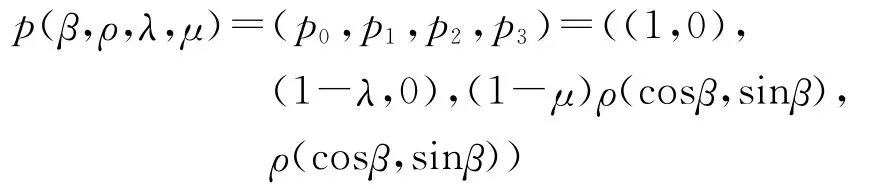
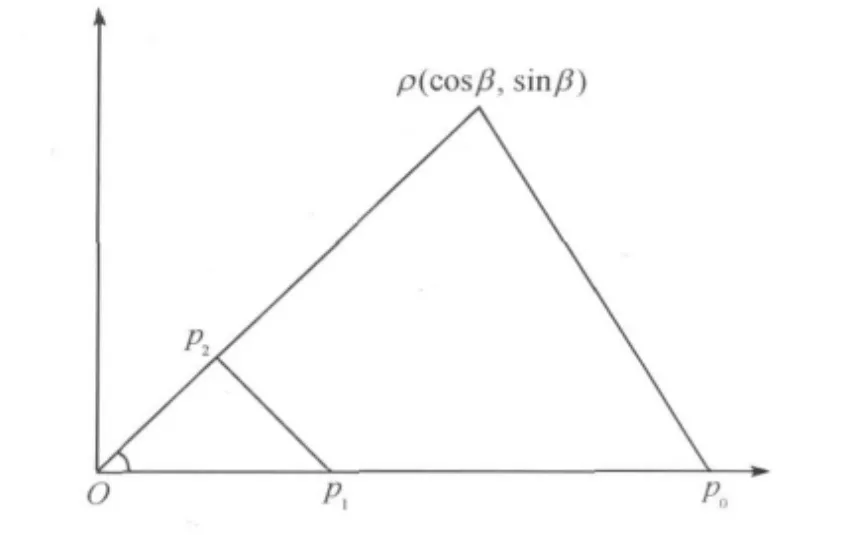
图2 曲线段的三角形凸包Δp0 Op3及其控制多边形p0 p1 p2 p3Fig.2 The triangle convex hullΔp 0 Op 3 of curve segment and its control polygon p0 p1 p2 p 3

将上面的各个点坐标代入（3）式，可以得到

下面的定理给出了当λ，μ取何值时，该控制多边形确定的C-Bézier曲线是PH曲线.

在［0，1；0，1］内的解，则由p0p1p2p3生成的四阶C-Bézier曲线是PH曲线.该方程是以λ，μ为未知数，由文献［9］知，它在［0，1；0，1］内必有一根.

3.2 误差分析

设A为代数曲线段，p（t）为插值曲线段，则给出如下误差定义.

定义2 在参数域［0，1］上取ti＝i／n，0≤i≤n，n∈N，记p（t）上的对应点为（x（ti），y（ti），A 上的对应点为（ti）（ti），定义插值误差为

3.3 算法的基本步骤

输入代数曲线A以及误差限δ，输出误差小于δ的分段插值PH-C曲线.

1）对原始代数曲线进行分段（涉及拐点、奇点和极值点的计算）.

2）计算代数曲线段A两端点处的切线，两切线交点的坐标以及两切线的夹角.

3）计算PH曲线的控制多边形.

若逼近误差e（A，p（t））＜δ，则计算过程终止，否则，将代数曲线段一分为二，递归调用上述分段逼近算法，直至满足给定的误差要求.

4 算 例

我们采用文献［10］中的例子，代数曲线（如图3

（a））为

图3 代数曲线C及其右四分之一分段Fig.3 The algebraic curve C and its right quarter part

我们以左上段为例，其中A（0，0），B（30／9，6／9），两切线交点O（6／9，6／9），可以算出β＝3π／4，ρ＝0.874 0.由文献［12］知，当α→0时，C-曲线的正规B基趋近于四次Bézier基.这里我们取α＝0.001，经计算，（λ，μ）＝（0.624 85，0.672 12）为方程组F（3π／4，0.874 0）在［0，1；0，1］内的解，根据（4）式可以就算出p1（0.170 1，0.170 1），p2（0.382 5，0.272 2），从而PH-C曲线的控制多边形也就确定了.图4是逼近效果图.其中：实线代表原曲线，虚线表示用PH-C曲线逼近的结果.

图5是误差函数曲线图.图5中（a—d）分别表示代数曲线左上段，右上段，左下段和右下段的逼近误差.

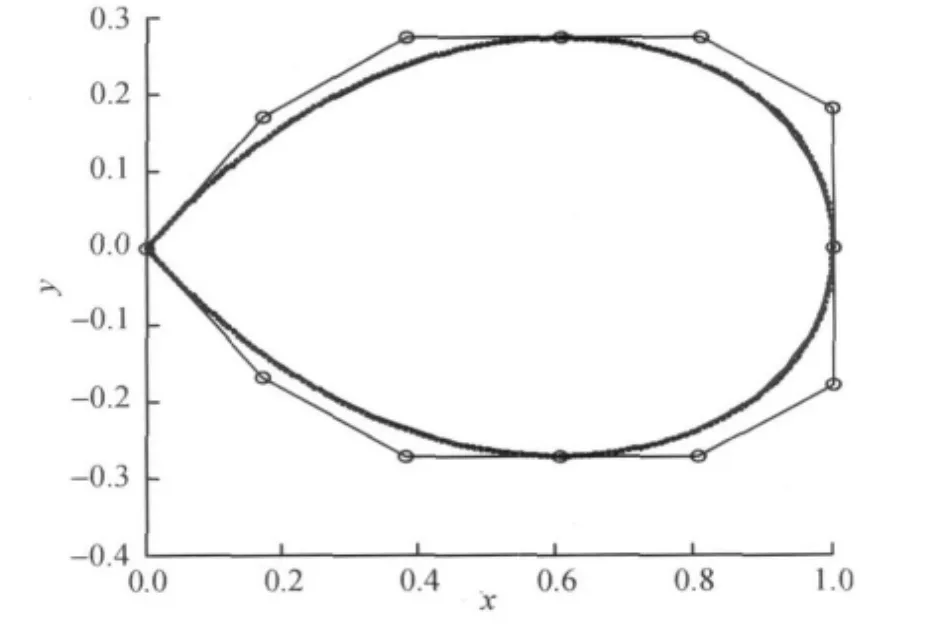
图4 代数曲线的PH-C曲线逼近Fig.4 The PH-C curve approximation of algebraic curve

图5 误差函数曲线图Fig.5 The error function curve

5 结 论

PH-C曲线具有同Bézier曲线类似的性质：端点插值性质，导矢性质，凸包性，离散性质，变差缩减性等.然而PH-C曲线能表示一些Bézier曲线不能精确表示的曲线：如圆弧，椭圆，正弦曲线等.由于PH-C曲线综合了Bézier曲线，PH曲线以及C曲线的许多优良性质，从而比Bézier曲线，PH曲线以及C曲线有着更加广泛的应用.我们用三次PH-C曲线逼近代数曲线，算法简单有效，插值曲线保持了原曲线的凹凸性，单调性，G1连续性等重要几何性质，通过算法的递归调用，可以将逼近误差控制在给定的范围之内.

［1］FAROUKI R T，SAKKALIS T.Pythagorean hodographs［J］.IBM Journal of Research and Development，1990，34（5）：736-752.

［2］FAROUKI R T，SAKKALIS T.Pythagorean-hodograph space curves［J］.Advances in Computational Mathematics，1994，2（1）：41-66.

［3］DIETZ R，HOSCHEK J，JUTTLER B.An algebraic approach to curves and surfaces on the sphere and on other quadrics［J］.Computer Aided Geometric Design，1993，10（3／4）：211-229.

［4］郑志浩，汪国昭.用三次PH曲线构造平面Bézier曲线的等距线算法［J］.计算机辅助设计与图形学学报，2004，16（3）：324-330.

［5］ZHANG Ji-wen.C-curves：an extension of cubic curves［J］.Computer Aided Geometric Design，1996，13（3）：199-217.

［6］ZHANG Ji-wen.C-Bézier curves and surfaces［J］.Graphical Models and Image Processing.1999，61（1）：2-15.

［7］ZHANG Ji-wen.Two different forms of C-B-splines［J］.Computer Aided Geometric Design.1997，14（1）：31-41.

［8］MORIN G，WARREN J，WEIMER H.A subdivision scheme for surfaces of revolution［J］.Computer Aided Geometric De-

sign，2001，18（5）：483-502.

［9］陈文喻，曹娟，汪国昭.Pythagorean-Hodograph C-曲线［J］.计算机辅助设计与图形学学报，2007，19（7）：822-827.

［10］胡斌，梁锡坤.代数曲线的分段有理二次B样条插值［J］.计算机工程与应用，2007，43（24）：55-58.

［11］黄群宾，邓鹏.一种求代数曲线的切线与渐近线的初等方法［J］.四川师范学院学报，2001，22（4）：389-391.

［12］陈秦玉，杨勋年，汪国昭.四次C-曲线的性质及应用［J］.高校

应用数学学报：A辑，2003，18（1）：45-50.

PH-C curve approximation of planar algebraic curves

SHOU Hua-hao1，JIANG Yu1，MIAO Yong-wei2
（1.College of Science，Zhejiang University of Technology，Hangzhou 310023，China；2.College of Computer Science and Technology，Zhejiang University of Technology，Hangzhou 310023，China）

Approximate parameterization of algebraic curve is an important topic in computer aided geometric design and graphics.PH-C curve inherits all the good quality from Bézier curve，PH curve and C curve，therefore PH-C curve approximation of algebraic curve is necessary.The algebraic curve is segmented according to convexity and monotonicity，the control polygon is constructed based on angles between two tangent lines and the line connecting two end points.A detailed algorithm is proposed to approximate algebraic curve with piecewise degree 3 PH-C curve.The approximate PH-C curve keeps some important geometric features of the original algebraic curve such as convexity、monotonicity and G1continuity.The approximation error can be controlled by means of recursively use of the algorithm.Numerical experiments show that the algorithm provided an efficient approach to approximate parameterization of algebraic curve.

algebraic curve；PH-C curve；curve approximation

TP391.7

A

1006-4303（2012）01-0111-04

2010-10-15

国家自然科学基金资助项目（61070126，61070135）；浙江省自然科学基金资助项目（Y1100837）

寿华好（1964－），男，浙江诸暨人，教授，博士，研究方向为计算机辅助几何设计与图形学，E-mail：shh＠zjut.edu.cn.

（

刘 岩）