基于层次分析法的工程建设方案优选

2012-08-24 03:15章林，李乐

科学之友 2012年15期

章林，李乐

（空军第一建筑安装工程总队，北京 100076）

层次分析法（简称AHP）是美国匹兹堡大学教授A.L.Saaty于20世纪70年代提出的一种系统分析方法，是一种定性和定量相结合的、系统化的、层次化的分析方法。层次分析法的整个优选过程体现了人的决策思维的基本特征，即分解、判断与综合，便于决策者之间彼此沟通，是一种十分有效的系统分析方法，广泛地应用在经济管理规划、能源开发利用与资源分析、城市产业规划、人才预测、交通运输、水资源分析利用等方面[1]。

本文将AHP运用在工程建设方案优选方面，构建了使用性能、工期性能、经济性能和对当地的影响等4个主准则和9个子准则。

2 工程建设方案优选的AHP模型

2.1 目标层

目标层又称最高层，为分析问题的预定目标或理想结果。对于工程建设方案优选问题，目标层则为选择最优的工程建设方案，作为决策者的科学参考依据。

2.2 准则层

准则层又称中间层，这一层次中包含了为实现目标所涉及的中间环节，它可以由若干个层次组成，包括所需考虑的主准则和子准则。结合工程实际经验，本文提出工程建设方案优选AHP模型的准则层因素，包括4个主准则和9个子准则，它们是：①工程的使用性能，包括耐久性、功能性和安全性；②工程工期，包括工艺复杂程度和协调复杂程度；③工程造价，包括单位工程费用和使用维护费用；④工程对当地的影响，包括征地拆迁移民量和对环境的影响程度。

2.3 方案层

方案层又称最底层，包括了为实现目标可供选择的各种措施、决策方案等。由此，工程建设方案优选的AHP模型见图1所示。

需要指出的是，主准则和子准则并非是完全支配与被支配的关系，如征地拆迁移民量可以影响工期，功能性可以影响工程造价等；因此，针对具体工程方案优选，可以考虑子准则直接对目标层建立判断矩阵。

3 准则层判断矩阵的建立

3.1 专家会议法

需要指出的是，对于每一个工程，其都有侧重点，比如国防工程侧重工期和使用性能、城市改造工程侧重对当地的影响等。因此，在对工程方案进行优选时，根据实际情况，需采用专家会议法，根据专家对实际工程情况的分析，对9个子准则的重要性进行量化排序，最终形成准则层判断矩阵。

图1 工程建设方案的AHP模型

3.2 判断矩阵的建立

假设现在要比较9个准则对目标层的影响大小，为提供可信的数据，可以采取对因子进行两两比较，建立成对比较矩阵的办法[2][3]。即每次取两个准则xi和xj，以aij表示xi和xj对目标层的影响大小之比，全部比较结果用矩阵A=（aij）9×9表示，A即为判断矩阵。容易看出，若xi和xj对目标层的影响之比为aij，则xi和xj对目标层的影响之比应为aji=1/aij。

关于如何确定aij的值，Saaty等建议引用数字1～9及其倒数作为标度。表1列出了1～9标度的含义。

由此，判断矩阵可表示为：

表1 层次分析法准则之间重要性比较量化

式中：n=9。

3.3 权向量的计算和一致性检验[4]

计算判断矩阵的最大特征根λmax和特征向量，并作一致性检验。若通过，则特征向量为权向量W，并经归一化后即为同一层次相应因素对于上一层次中的某因素的相对重要性的排序权值，权向量W中的每个这一过程称为层次单排序。

经过归一化后，成对比较阵A转化为式（2），其中，w是由第p层对第p-1层权向量。

表2 RI随因素个数n的变化规律

4 方案层判断矩阵的建立

方案层判断矩阵应以每个准则作为依据，两两比较得出判断矩阵。假设有3个候选方案，分别为f1、f2、f3，考察3个方案的耐久性分别为 n1、n2、n3，则判断矩阵为：

对于其余准则的判断矩阵建立方法与此类似，则对于方案层，共建立9个判断矩阵。

5 计算方案层组合权向量

5.1 计算方案层总排序

准则层和方案层的判断矩阵确定后，需计算各方案对于目标的排序权重，从而进行方案优选。

设准则层（A层）包含A1，…Am共m个因素，它们的层次总排序权重分别为a1，…am；设其后方案层（B层）包含n个因素B1，…，Bn，它们关于Aj的层次单排序权重分别为b1j，…，bnj（当Bi与Aj无关联时，bij=0）。现求B层中各因素关于总目标的权重，即求B层各因素的层次总排序权重b1，…，bn，计算按表3所示方式进行，即

表3 总排序计算方法

5.2 计算方案层组合权向量

对层次总排序也需作一致性检验，检验仍如层次总排序那样由高层到低层逐层进行。设B层中与Aj相关的因素的成对比较判断矩阵在单排序中经一致性检验，求得单排序一致性指标为CI（j），（j=1，…，m），相应的平均随机一致性指标为RI（j）CI（j）、RI（j）已在层次单排序时求得，则B层总排序随机一致性比为：

6 某阵地截排洪工程应用实例

6.1 工程概况

该工程处于鄂北丘陵地区，场区所在区域的地形呈波状起伏，丘陵川谷相间，沟谷纵横、自然地面标高相对高差一般在23～56 m，最大高差达78 m。场地总趋势为西南高、东北低。场区内有4条主要冲沟。在规划该截排洪方案时，首先比选了3个平面布置方案：排洪涵洞穿越场区（穿越方案），场外截洪沟绕行（绕行方案），中间穿越、两侧绕行（穿绕结合方案），以确定截、排洪设施路由的主要走向，并便于后续的路由细部优化。截排洪规划方案如图2所示。

图2 截排洪规划方案

穿越方案的路由总长2 239 m，都是涵洞，施工难度大，并在施工过程与场区土方工程施工中的干扰很大，工期难以保证。

绕行方案不在场区修建涵洞，避免了与土方工程的相互干扰，但排洪沟的路由经过多个高度近30 m的山丘，如果采用明沟开挖，上口宽度近100 m，土方量很大。如果采用隧洞穿越，需要设置隧洞1 353 m，明渠2 184 m。整个工程的施工比较复杂，工期较长。方案中排洪沟施工虽然不直接干扰场区土方施工，但在雨季到来之前，如果隧洞完不成，将会导致上游冲沟中的雨水无法排出，也会影响场区土方施工。

穿绕结合方案中穿越场区的涵洞长683 m，覆土11 m左右。两侧绕行的截、排洪设施中，隧洞总长约530 m，且每段比较短，最长218 m，明渠需要1 649 m。方案中大部分截、排洪设施的施工与阵地场区的土方施工不会产生交叉，施工难度小，工期较短，另外，减轻了下游的洪水负担；降低了对附近农田等设施的危害[6]。

6.2 准则层判断矩阵构建

根据工程具体情况分析，构建准则层判断矩阵为：

该判断矩阵的最大特征值和特征向量分别为：λmax=9.003 6，V=[0.021 0 0.037 9 0.060 6 0.084 7 0.101 8 0.11 2 0.145 6 0.174 7 0.261 8]T。

检验一致性：

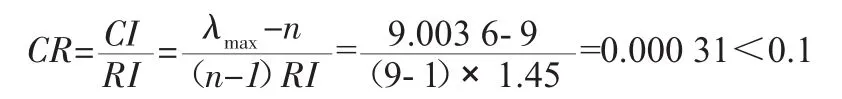
所以，判断矩阵的一致性是可以接受的。

6.3 方案层判断矩阵构建

6.3.1 耐久性指标

穿越方案采用的钢筋混凝土涵洞使用年限为50年[5]；绕行方案采用钢筋混凝土隧洞和浆砌块石明渠，其中隧洞1 353 m，明渠 2 184 m，综合使用年限 =（1 353×50+2 184×10）/3 537=25.3年；穿绕结合方案采用涵洞683 m，隧洞530 m，明渠1 649 m，综合使用年限 =（1 213×50+1 649×10）/2 862=26.95年，构建的比较矩阵为：

判断矩阵的一致性可以接受。

6.3.2 功能性指标

穿越方案中的构筑物只完成疏导径流的基本功能，而绕行方案和绕穿结合方案中的明渠兼备有围界的功能，计算出方案的功能性指标后，构建比较矩阵为：

判断矩阵的一致性可以接受。

6.3.3 安全性指标

穿越方案中的涵洞都从阵地场区通过，一旦出现破坏后，会对整个主体工程的功能实现产生严重影响，因此，其安全性指标为4；绕行方案中的构筑物都远离阵地场区，出现破坏后会导致洪水淤积在主体工程前，虽然对主体工程功能实现不产生严重影响，但是冲刷阵地边坡会对边坡造成较大影响，其安全性指标为2；绕穿结合方案中既有穿越阵地场区的涵洞，也有远离场区的明渠、隧洞，通过加权计算安全性指标后，构建比较矩阵为：

判断矩阵的一致性可以接受。

6.3.4 工艺复杂程度指标

穿越方案中的涵洞都采用钢筋混凝土现浇而成，而且因位于自然冲沟中，需要对涵洞的基础进行地基处理，估测每延米涵洞需要15人×8个工作日（含地基处理）乘以工程量2 239 m，就可以得出所需要的总人数工日；绕行方案中的明渠和隧洞都不需要进行地基处理，但经过节理发育山体的隧洞，需要增加钢格栅支撑及加大喷锚支护构力度，估测每延米隧洞需要13人×7个工作日，经过与不同形式的构筑物综合计算后得出所需要的总人数工日；绕穿结合方案中的周家冲涵洞每延米需要14人×8个工作日（含地基处理），外围的隧洞和明渠每延米分别需要10人×5个工作日、15人×8个工作日、3人×0.4个工作日，综合计算后，构建比较矩阵为：

判断矩阵的一致性可以接受。

6.3.5 协调复杂程度指标

穿越方案中的涵洞所处位置属于征地范围，施工时与周围的居民不发生联系，只会与主体工程的施工发生交叉，因而其协调复杂程度指标为1；绕行方案中的明渠需要拆迁部分居民、占用周围百姓的耕地、农田水利设施，隧洞的出入口需要占用山体中的自然植被，其综合协调复杂程度指标=（1 353×3+2 184×4）/3 537=3.62；穿绕结合方案中的涵洞在施工时需要与主体工程进行协调，两侧绕行的明渠、隧洞在施工时需要征地拆迁等协调，其综合协调复杂程度指标 =（658×1+530×3+1 649×4）/2 837=3.12，构建比较矩阵为：