离散时间沿高优先队列的尾部渐近性分析

张华娟

（无锡南洋职业技术学院 江苏 无锡 214081）

0 前言

二维马氏链系统的尾部渐近性便于估计，能提供稳态概率的信息和边界。优先队列系统的应用广泛，有很重要的地位。经典的一个服务台、两种顾客的优先队列系统已有很多人研究。人们经常参考Miller[1]，其它优先队列模型有Gail,Hantler和Taylor[2],Drekic and Woolford[3]等。

本文考虑离散时间、离散状态的系统，它可以看作取可数状态的离散QBD。特别地，本文研究强占优先制队列。对应于经典的连续时间模型，该模型被应用在计算机和通信网络方面。运用矩阵分析法，得到了联合稳态概率沿较高优先队列的衰减速率。

1 模型及定理

本文考虑一个服务台、两类顾客的离散时间优先队列。在每个时刻，下面的三件事都相互独立：

（a）第一类顾客到达概率为 0＜p＜1；

（b）第二类顾客到达概率为 0＜q＜1；

（c）服务台对这两类顾客的服务率都是0＜r＜1（如果没有顾客，则不服务）。

Q1（n）和 Q2（n）分别代表系统中第一类（高优先）和第二类（低优先）的顾客数。 显然，{（Q1（n），Q2（n））；n=0，1，2，…}是一个离散时间齐次马氏链。本文以系统中高优先队列的顾客数Q1（n）作为水平坐标，得该马氏链的转移图，见图1。

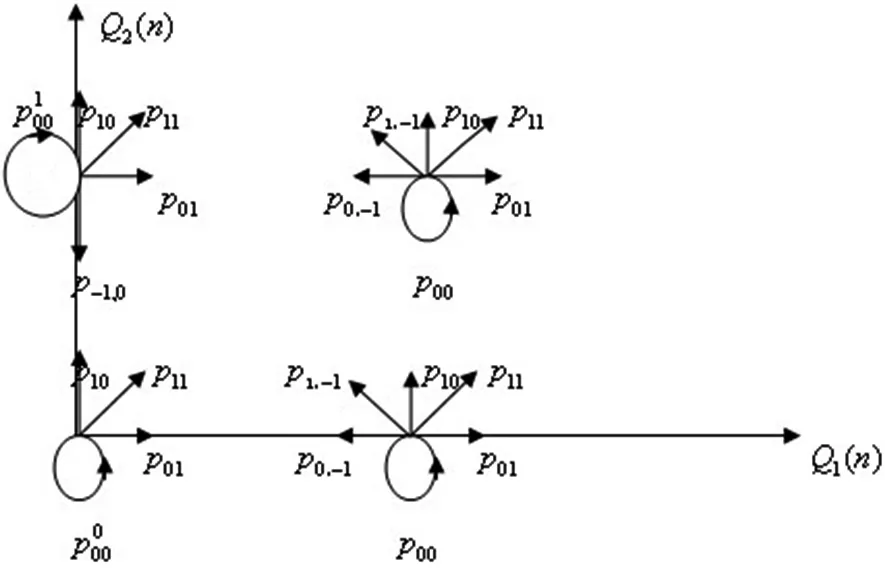
图1 沿高优先队列马氏链的转移图

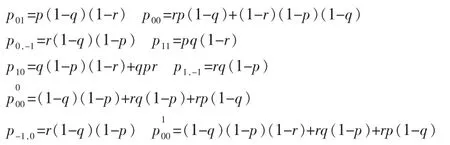
设该系统中较高优先队列和较低优先队列的联合稳态概率为πij，把 πij水平分成 π=（π0，π1，…），其中 πi=（πi0，πi1，…）。 设较高优先队列的边缘分布为π（h）n。

用矩阵分析法，该马氏链的转移概率矩阵P˜可以分成如下的块结构：

如上文所述，极导线与接地极线共塔架设线路存在由雷击引起双极闭锁的潜在风险。主要有两种情况：一种是很大的雷电流击中杆塔或地线，极导线闪络跳闸的同时，接地极线路也出现了闪络，此时若故障极重启失败而接地极线路又无法熄弧，则将出现双极闭锁；另一种是较大的雷电流绕击极导线，极导线发生闪络跳闸的同时，共塔接地极线路由于感应过电压也发生闪络，此时若故障极重启失败而接地极线路仍无法熄弧，则将出现双极闭锁。针对这两种情况，本节对降低双极闭锁概率的措施进行探讨。

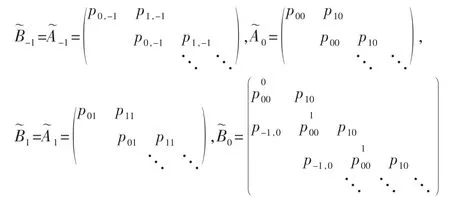
定理 带强占型优先权的双队列Geom/Geom/1排队系统，满足ρ＜1 时有，

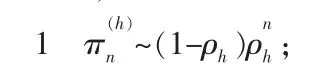
其中 r0，r1分别见（4）式，（5）式，并且 πn，j的轻尾衰减率是 r0。

2 定理证明

Miller[1]把该系统作为拟生灭过程，其矩阵几何解有速率矩阵Rh，且满足

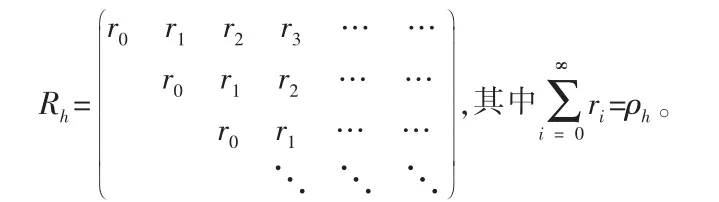
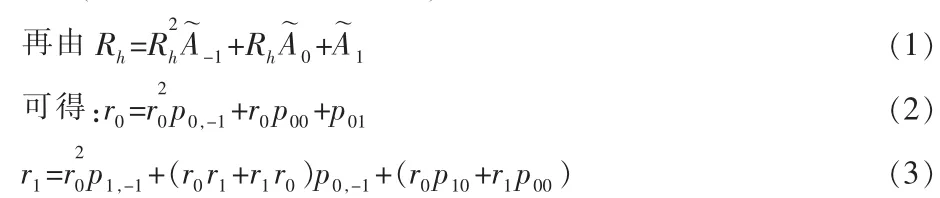
由于Rh是上面矩阵公式的最小非负解，故

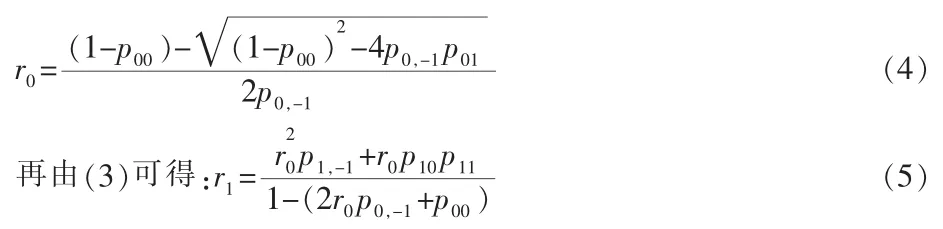
根据 ri的性质和矩阵几何解，显然有

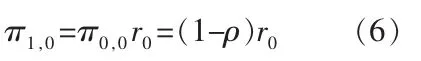
其在确定衰减系数的证明中将用到。

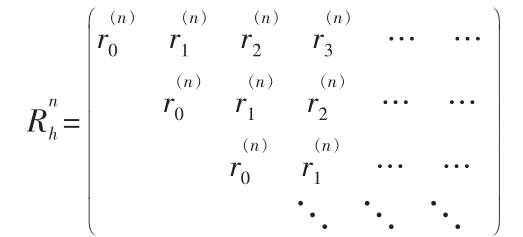
它满足下面的矩阵几何解

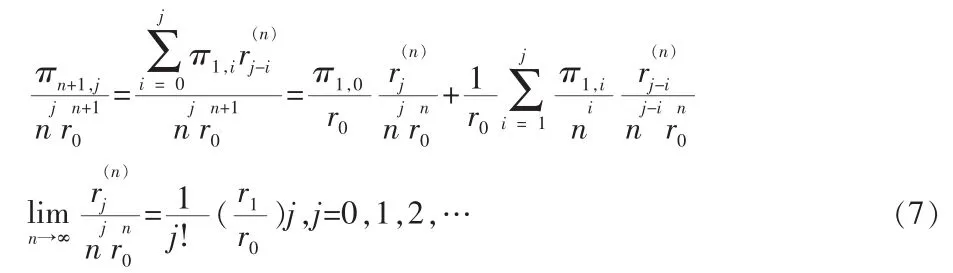
之前表达式右边的第二项趋于0。再由（6）式，结论得证。

下面用归纳法证明（7）式。当j=0，（7）式显然成立。假设对任意j≤k，（7）式成立，下面证明当 j=k+1 时，（7）式也成立。

通过反复运用 r（n+1）k+1的定义，得到

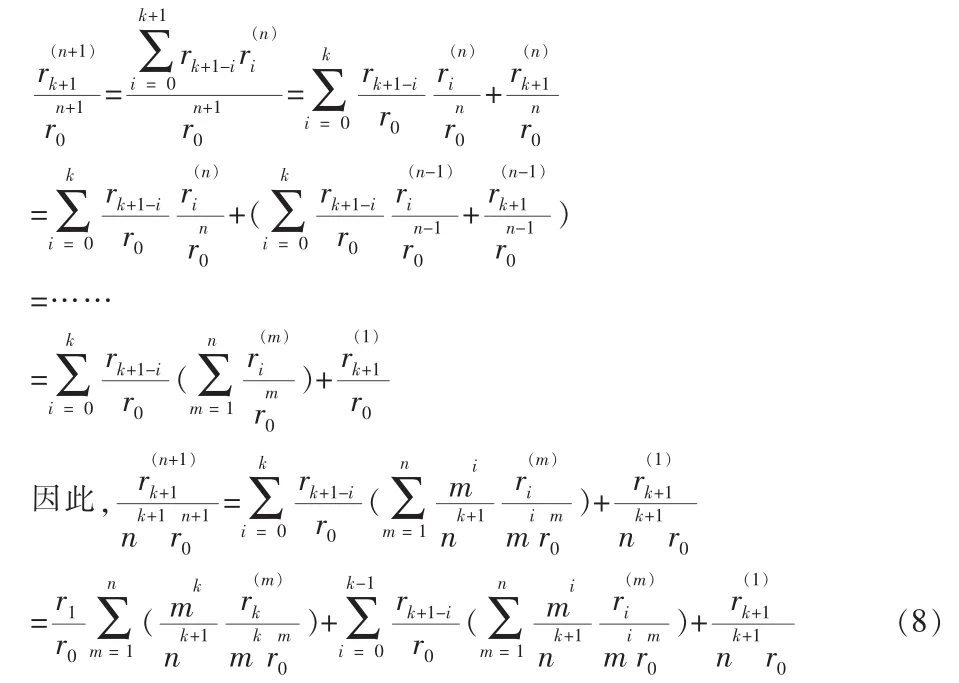
当n→0时，（8）式第三项显然趋于0。下面证明（8）式第二项趋于0。

事实上，由归纳假设

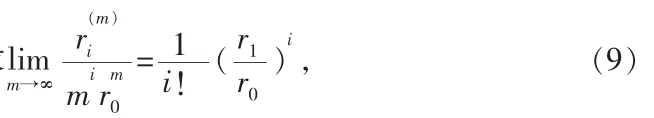
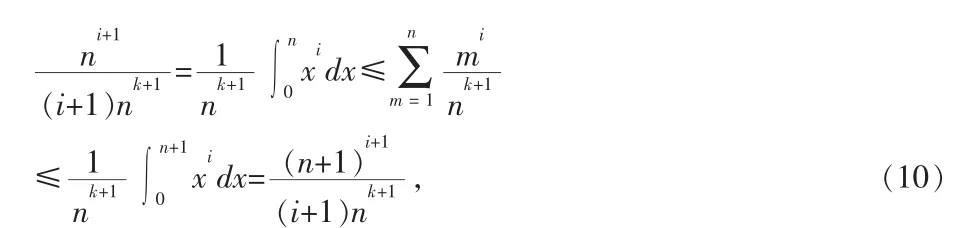
该式在证明的最后一步将被用到。

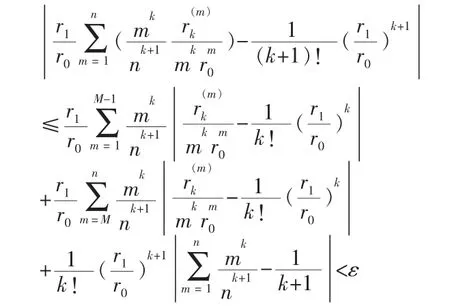
由（11）式，上面不等式中间部分的第三项可以任意小。由归纳假设（9）式，可以取M＞0，使得当 m≥M 时，任意小，再由（11）式，可得第二项任意小。对于有限的M，当n足够大时，第一项显然任意小。

［1］Miller,Douglas R.Computation of steady-state probabilities for M/M/1 priority queue[J].Operations Research,1981,29(5)：945-958.

［2］Gail,H.R.,Hantler,S.L.and Taylor,B.A.On preemptive markovian queue with multiple servers and two priority classes[J].Mathematics of Operations Research,1992,17：365-391.

［3］Drekic,S.and Woolford,D.G.A preemptive priority queue with balking[J].European Journal of Operational Research,2005：164,387-401.