一类生化反应动力系统的定性分析

张瑞海

(天津科技大学理学院，天津300222)

1 引言

随着微分动力学的发展，其作为一种研究实际问题的一种重要工具，已经渗透到各个领域.本文考虑了生化反应中的一个动力系统

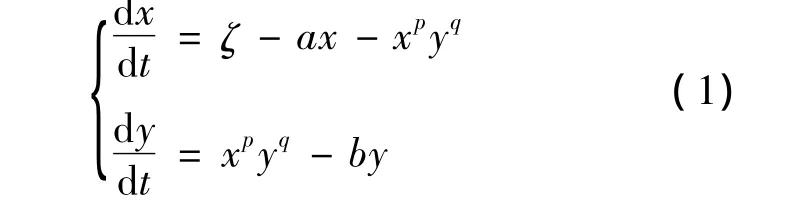
其中:ζ，a，b均为正常数，p，q 为正整数.对于系统(1)好多学者已经做了研究，如文献[1－6]讨论了a=0，p=1，q分别为 2，3，4，5，6 的情况，本文考虑了a=0，p=1，q=7的情况.进一步完善了系统(1)的定性分析.

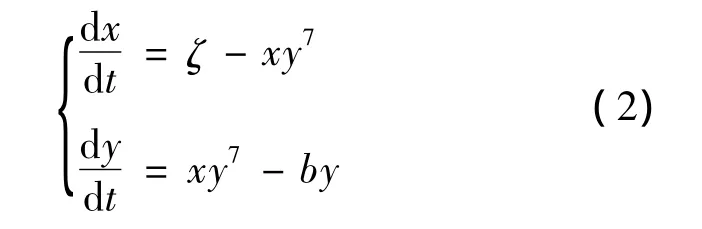
根据系统的实际意义有 x＞0，y＞0，ζ＞0，b＞0.令并且仍以 x，y，t记 u，v，τ.则上式化为

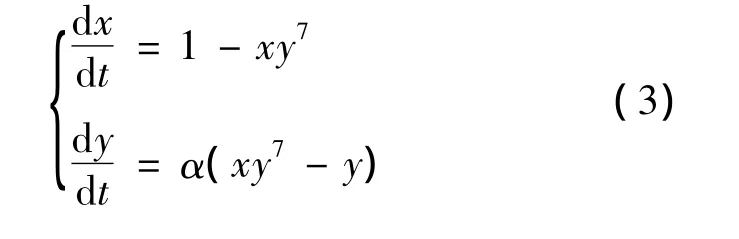
即(1，1)为系统的惟一平衡点.并且

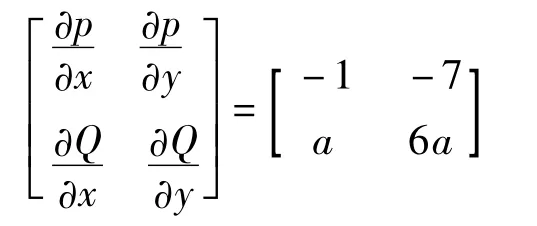
所以系统(3)在点A(1，1)处线性部分的特征方程为

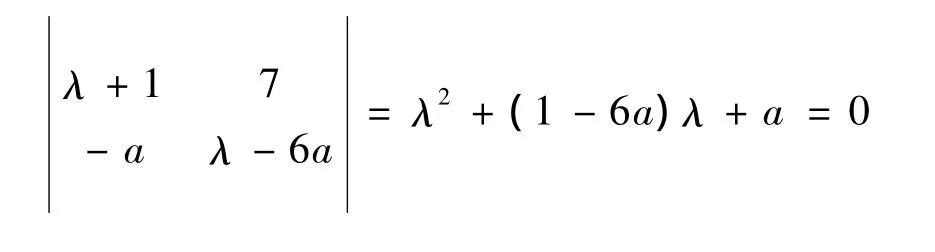
该方程有两个根

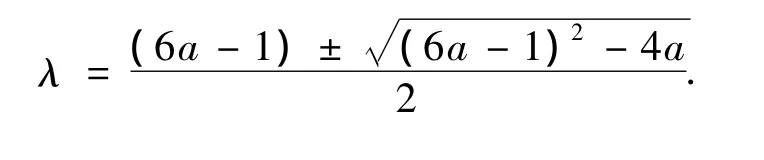
2 预备引理

引理1:

令 u=y－1，v=a(x－1)+y－1，则系统(3)化为

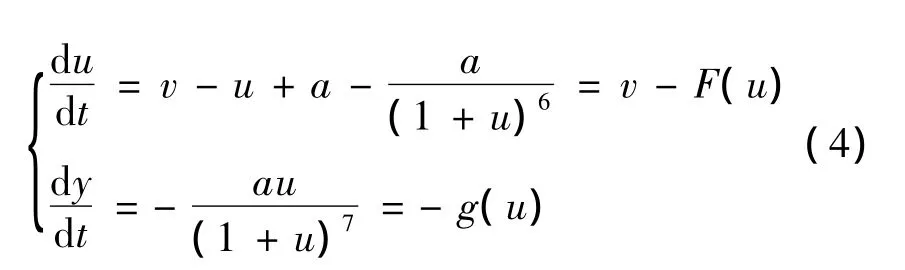
引入菲里波夫变换

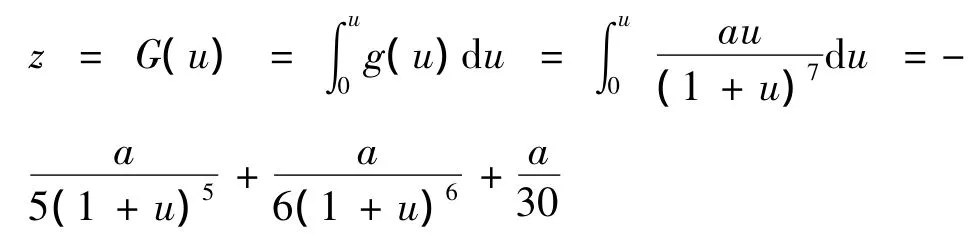
引理2:

证明:Φ(z)=F1(z)－F2(z)令，则Φ(0)=F1(0)－F2(0)=0

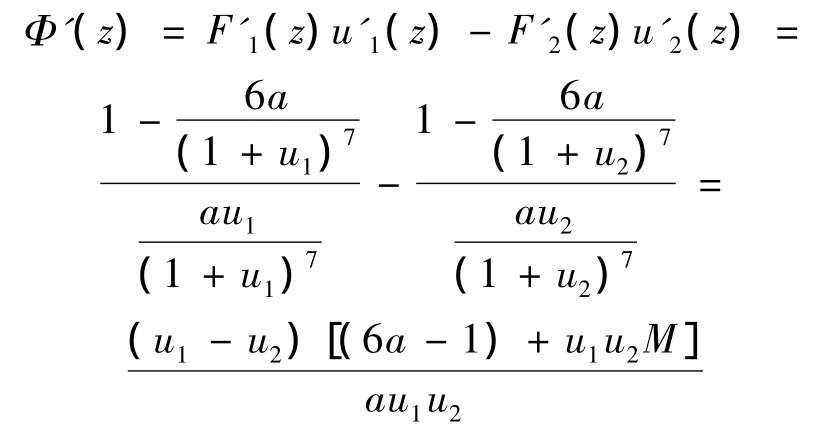
其中:

注意到 －1＜u2＜0＜u1，从而 u1u2＜0，u1－u2＞0，经计算M＞0，所以Φ'(z)＞0，也即Φ(z)=Φ(z)－Φ(0)=Φ'(z)z＞0，即 F1(z)＞F2(z).引理得证.

引理3:系统(3)在x＞0上没有垂直渐近线.

证明:采用反证法，假设引理3不成立，则∃x0＞0使得x→x0时y→±∞，而且;另一方面，注意到xy7－1，1－xy7均为连续函数，于是由系统(3)知不会有.矛盾，所以引理(3)成立.

3 主要结果及证明

证明:根据Bendixson环域定理，由引理1知，当a＞时，系统(3)的奇点A是不稳定的.为了证明定理2，只要再构造一个包围正奇点A的外境界线Γ*，随t的增加，使得系统(3)的轨线与Γ*相交时都从外部穿入外境界线Γ*内部.

令 Γ1:1－xy7=0，Γ2:xy7－y=0

其图形如图1所示，则系统(3)相平面的第一象限被Γ1，Γ2分成了四个区域.容易判断系统(3)在这四个区域中所确定的方向场分别为:

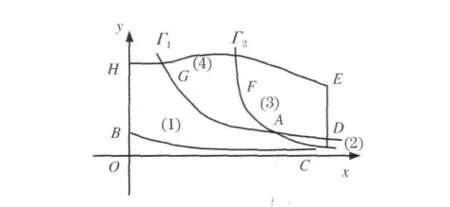
图1 第一象限被Γ1，Γ2分成四区域图

由方向场(1)知，存在y轴上的点B，使得系统(3)的过点B的正半轨一定向x轴的正向移动.又因为奇A点为系统(3)的不稳定奇点，从而该正半轨不会趋向奇点A.直线y=0是系统(3)的积分直线，从而该正半轨也不会与x轴相交.由引理(3)知系统(3)在x＞0上没有垂直渐近线，而Γ1，Γ2都以x轴为水平渐近线，由方向场理论知系统(3)的过点B的正半轨一定与Γ1，Γ2分别相交于C，D.然后过点D作平行于y轴直线DE.由向量场(3)知，在直线DE上，又注意到 y轴是 Γ1，Γ2的垂直渐近线，所以系统(3)的过点E的正半轨一定与Γ1，Γ2交于点F，G.最后过点G作x轴的平行线交y轴于点H，易知在直线GH上于是曲线

Γ*=BCDEFGHB

就构成系统(3)的包围正奇点的外境界线.定理2成立.

4 结语

对于系统(1)随着的增大计算量也越来越大，本文在文献基础上考虑了a=0，p=1，q=7的情况.应用微分方程定性理论对其奇点进行了分类，得到了其极限环不存在存在的系数条件，进一步完善了系统(1)的定性分析.

[1]CHENG L S.Nonlinear biological system[M].Beijing:Science Press，1993:22 －24.

[2]ZHANG J Y.Qualitative analysis of kind of nonlinear equation in biochemistry reaction[J].Acta Mathematics Applicatate Sinaca，1982，5(3):234－240.

[3]张芷分.微分方程定性理论[M].北京:科学出版社.1985.

[4]卓相来.一类生化反应模型极限环的存在唯一性[J].山东科技大学学报，2004，23(2):80－82.

[5]卓相来.一类生化反应动力系统极限环的存在唯一性[J].中国海洋大学报，2005，35(3):429 －431.

[6]陈成美.一类生化反应模型的定性分析[J].安徽工业大学学报:自然科学版，2011，28(1):97－100.