非线性最小二乘估计的蚁群遗传融合算法
陈 伟
(武汉科技大学城市建设学院,湖北 武汉 430070)
0 引言
近年来,现代智能优化算法,因其高效的优化性能、无需特殊新问题等优点,受到各领域的广泛关注和应用。诸如神经网络、遗传算法、蚁群算法、模拟退火、禁忌搜索、粒子群优化算法等。这些算法大大丰富了现代优化技术,也为具有非线性、多极值等特点的复杂函数及组合优化问题提供了切实可行的解决方法,但是每一种算法都有其自身的优势和缺陷,如何优势互补融合各类智能算法已成为研究重点。
遗传算法(Genetic Algorithm)是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。蚁群算法(Ant Colony Algorithm)是一种源于大自然生物世界的新型仿生类算法,20世纪90年代初由意大利学者Dorigo依照蚂蚁觅食原理设计而成的一种群体智能算法。由于该算法具有与其他算法比较易于结合等特点,诸多的改进算法被研究者提出以改善其本身的性能,与遗传算法结合是目前较流行的改进方法之一。本文利用遗传算法与蚁群算法的优势互补,将基于蚁群算法的混合遗传算法用于非线性最小二乘估计中。
1 非线性最小二乘估计的目标函数
由文献[1]知测量数据处理中的非线性模型,可用数学公式表示为:

其中,f(X)为未知参数向量X的函数,f(X)=(f1(X),f2(X),…,fn(X))T;L为n×1的观测向量;X为t×1的未知参数向量;Δ为n×1的观测误差向量。
非线性模型式(1)相应的误差方程可写为:

设观测值的权矩阵为n×n的对称正定矩阵P,则式(1)的非线性最小二乘估计问题可转化为:

由于LTPL为一常量,所以式(3)等价于:

式(4)即为非线性最小二乘估计的目标函数。
2 蚁群遗传混合算法设计
2.1 遗传算法简介
遗传算法(Genetic Algorithm)最初是由美国的J.Holland教授于1975年受生物进化论的启发提出的,它是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。在遗传算法中,将代表问题的解用染色体编码,种群为若干染色体的集合,代表问题解空间中若干解的集合,适应度为染色体的评价值,代表对解质量优劣的评价标准。在初始种群产生后,按照适者生存,优胜劣汰的原理,在每一代选择性能优异的个体,对其使用交叉、变异算子,产生出新的种群,如此不停迭代,最终寻找到最佳适应环境的个体;最后,将染色体解码,即可得到问题的最优解。
标准的遗传算法一般由以下几部分组成:参数编码、初始种群的设定、适应度函数的设计、遗传算子(选择、交叉、变异)的设计以及控制参数设定等。
2.2 蚁群算法简介
蚁群算法(Ant Colony Algorithm)是一种模拟蚁群觅食行为,采用信息素指引蚂蚁前进时方向,并利用正反馈机制进行搜索的计算智能算法。算法由许多蚂蚁共同完成,每只蚂蚁在候选解的空间独立搜索解,在所寻得的解上留下一定的信息素,并且感知其他蚂蚁释放的信息素,倾向于选择信息素浓度较高的节点。大量蚂蚁的集体行为表现出一种信息正反馈现象:某一节点上走过的蚂蚁越多,后者选择此节点的概率越大。
2.3 混合算法设计
为了克服两种算法各自的缺陷,形成优势互补。蚁群遗传融合算法的基本思路是将遗传算法引入到蚁群算法的初始信息素设置中,首先利用遗传算法的快速性、随机性、全局收敛性,产生有关问题的初始信息素分布,从而弥补了蚁群算法初期信息素匮乏导致搜索初期信息素积累时间较长的缺陷,加快了求解速度。接着采用蚁群算法,充分利用蚁群算法的并行性、正反馈机制、求解效率高等优点进行求解。该混合算法的关键是保证遗传算法和蚁群算法在最佳时机融合。本文采用的方法是:设置遗传算法的最小迭代次数nmin和最大迭代次数nmax,在遗传算法迭代过程中比较个体适应度值的变化,如果个体的适应度值变化较小,则说明此时遗传算法优化速度已较低,此时可终止遗传算法过程,进入蚁群算法。
非线性最小二乘估计的蚁群遗传混合算法设计步骤如下:
1)参数的初始化。确定种群规模G,设定交叉概率Pc、变异概率Pm等参数,随机产生初始种群。
2)定义目标函数和适应度函数,计算每一个体的适应度fi,对种群中的个体执行以下遗传操作,产生下一代个体:
a.选择操作。
选择算子采用轮盘赌选择方法,个体适应度越大,其被选中的概率就越高,反之亦然。若群体规模为G,按计算出群体中各个个体选择概率后,就可以决定哪些个体被选出。
b.交叉操作。
本文采用实数编码,交叉操作采用算术交叉算子,首先随机确认参与交叉的父代,并且进行两两配对,父代中的个体X和Y按照式(5)产生两个新的个体:

c.变异操作。
采用均匀变异算子。个体Xi的各基因位以变异概率Pm发生变异,即按概率Pm用区间[Xmin,Xmax]中均匀分布的随机数代替原有值。
3)反复执行第2)步操作,直至满足遗传算法结束条件。设置最小迭代次数nmin和最大迭代次数nmax,在遗传算法的迭代过程中同时统计进化率,其公式为:
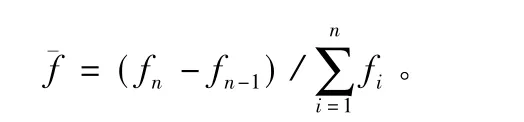
在设定的迭代次数范围内,若连续三次进化率都小于最小进化率时,则停止遗传算法迭代过程,进入蚁群算法。
4)当遗传算法按照规则执行结束后,选择适应能力强的个体放入新集合S中,作为优化解的集合。
5)根据优化解生成吸引强度初始分布,按蚁群算法信息素初值设置策略,计算信息素初值。初始化蚁群算法控制参数,设置蚁群算法结束条件,设置最大循环次数nc。
a.初始信息素设置。
本文采用比利时学者Thomas提出来的最大最小蚂蚁系统(MMAS)中的方法。信息素的初值设为 τS=τC+τG,其中,τC为根据具体求解问题给定的吸引强度常数;τG为遗传算法求解结果转换的吸引强度。
b.信息素更新规则。
τij(t)表示t时刻在路径ij上残留的信息量,用参数ρ表示信息素蒸发率,蚂蚁完成一次循环后各路径上的信息量更新规则为:τij(t+1) = (1 - ρ) τij(t) + Δτij(t); Δτij(t)=其中,Q为常数;Lmax为当前搜索的最长路径的集合;E为当前最短路径上的路径集合。
c.转移概率设置。
蚂蚁k在t时刻从当前节点i转移到节点j的转移概率定义如下:

其中,ηij为边路径(i,j)的能见度,一般取为1/dij;路径能见度的相对重要性为β(β≥0);路径轨迹的相对重要性为α(α≥0);allowed是第k只蚂蚁下一步可以选择的路径集。
6)将m只蚂蚁置于各自的初始节点,计算每只蚂蚁的转移概率Pij,根据转移概率移动每只蚂蚁到下一个节点,并进行信息素局部更新。
7)判断所有蚂蚁是否已形成完整路径,如还没有形成完整路径则转6),否则,执行8)。
8)更新全局信息素,更新全局最优解。
9)判断流程是否结束,若当前进化代数不大于nc,转6),否则输出最优解。
3 应用实例
本例取自参考文献[1]例2-1-1。已知非线性模型为Li=x1eix2,其中参数x1和x2的真值为 X=(5.420 136 187,-0.254 361 89)T。Li的5个真值(用参数的真值X算得)和相应的5个同精度独立观测值见表1。观测值的中误差σ0=±0.007 833。

表1 Li的真值和相应的观测值
观测方程为:Li=x1eix2+Δi(i=1,2,3,4,5)。
根据式(4)可知本例的目标函数为:
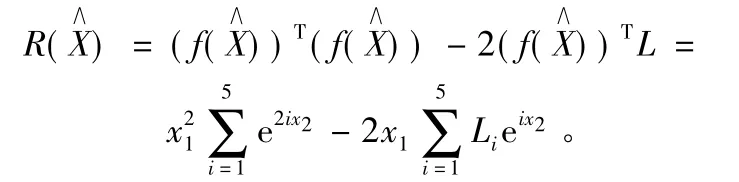
按照本文非线性最小二乘估计的蚁群遗传混合算法的思想和步骤编程实现本例的参数估计,其结果为:X=(5.422 735 546,-0.255 670 691)T,‖ΔX‖ =0.002 910 147。从计算结果可看出,用蚁群遗传混合算法计算出来的结果与真值相差很小。
4 结语
本文尝试将遗传算法和蚁群算法进行有效融合,并将该混合算法用于非线性的参数估计中。该混合算法利用遗传算法和蚁群算法的优势互补,使求解过程尽量避免了陷入局部最优同时提高了搜索效率,对解决非线性参数估计问题有一定的应用价值,值得进一步研究。
[1] 王新洲.非线性模型参数估计理论与应用[M].武汉:武汉大学出版社,2002:29-31.
[2] 申利民,高 洁.基于遗传蚁群融合算法的测试用例最小化研究[J].计算机工程,2012,38(16):57-64.
[3] 曹腾飞,符云清,钟明洋.融合遗传蚁群算法的Web服务组合研究[J].计算机系统应用,2012,21(6):81-85.
[4] 陈 伟,张从海.混合模拟退火——遗传算法在参数估计中的应用[J].地理空间信息,2007,5(2):99-101.

