独辟蹊径 追求卓越——2011年高考福建理综卷第22题赏析与拓展

曾湘咏

（株洲市教育科学研究院 湖南 株洲 412000）

2011年高考福建理综卷第22题摒弃了“重数学技巧，轻物理思维”传统做法，站在了物理学科的高度，体现了物理压卷题考物理思维的追求，从2011年众多物理压卷题中脱颖而出.试题以全新的物理图景为载体，新颖别致，巧妙设问，灵活、深刻地考查了学生物理思维，体现了命题者“独辟蹊径，追求卓越”的思想，是难得一见的高品质的压卷题.

题目：如图1（a）所示，在x＞0的空间中存在沿y轴负方向的匀强电场和垂直于xOy平面向里的匀强磁场，电场强度大小为E，磁感应强度大小为B.一质量为m，带电量为q（q＞0）的粒子从坐标原点O处，以初速度v0沿x轴正方向射入，粒子的运动轨迹见图1（a），不计粒子的重力.

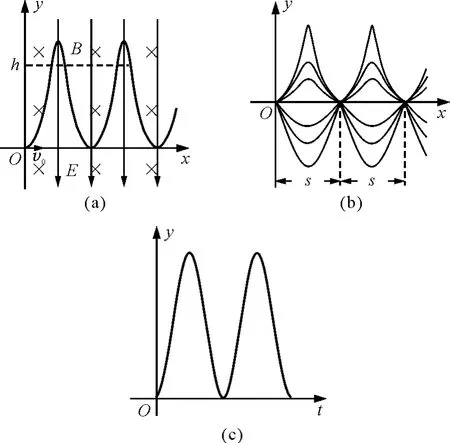
图1

（1）求该粒子运动到 ＝h时的速度大小v；

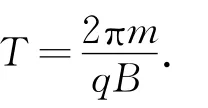
1）求粒子在一个周期内沿x轴方向前进的距离s；

2）当入射粒子初速度大小为v0时，其y-t图像如图1（c）所示，求该粒子在y轴方向上做简谐运动的振幅Ay，并写出y（t）的函数表达式.

参考答案：

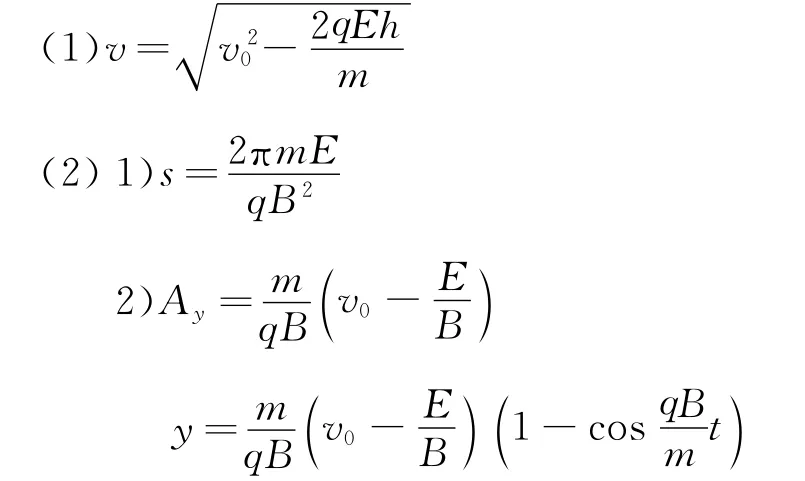
1 试题赏析

1.1 返璞归真 淡化数学技巧

数学对物理的重要性毋庸置疑，高考考试大纲就明确提出了考查学生“利用数学处理物理问题的能力”.然而，如果超越数学的工具性，片面强调数学技巧，势必会重数学技巧，轻物理思维，将物理异化为数学，从而既远离了物理的本质，又与物理教育的真谛背道而驰.2009年高考全国 Ⅰ 卷“粒子碰钢板”、1995年“抛沙包”等试题广受诟病就是此类原因.这两道题所涉及的带电粒子在匀强磁场中的圆周运动和动量守恒定律等物理知识众所周知，能运用繁难的数学运算技巧的却是寥若晨星.

的确，物理压卷题需要“对高分段的学生进行区分”，但用什么来区分和怎样区分是一个值得思考的问题.将“利用数学处理物理问题的能力”解读为“利用数学技巧甄别考生、考查能力”，则是一种误读.物理和数学的工具性的主仆关系不能颠倒，数学的工具性应表现“为物理”所用，而不是凌驾于物理之上.

这并非学科本位思想.中学物理，无论是教学还是考试，即便是高考这样倍受关注的选拔性考试，都应注重数学工具的普适性，而不是片面强调它的技巧性，这既符合中学生的实际，也符合中学物理教学的实际.反对重数学技巧，轻物理思维，并不意味着主张重物理思维，轻数学技巧，但至少应是物理思维，数学技巧并重，且重物理思维应是第一位的.

学生解答福建压卷题不需要任何数学技巧，但解答起来并不容易，为什么？因为物理思维的灵活性和深刻性并不比数学的技巧性容易，同样可以区分高分段的学生，而且，这样区分更合理、更到位，因而更有效，因为它站到了学科的高度，回归了物理本质，使物理压卷题成为一道物理难题，而不是数学难题.

物理压卷题应回归物理本质，重在考查学生物理思维的灵活性和深刻性，福建试题为怎样区分高分段学生指明了方向.

1.2 独辟蹊径 彰显学科品位

试题的素材可以说是“半旧半新”.说它旧，是因为带电粒子在电场和磁场中的运动，学生已司空见惯；说它新，是因为粒子在电场和磁场中既不做“类平抛”运动，也不做圆周运动.试题直接展现了两幅关于粒子运动轨迹的全新图景，如图1（a）、（b）所示.学生面对陌生的图景，视觉受到冲击，心理平衡被打破，已有知识和新的问题发生碰撞，探究欲望被激发，于是，试题润物无声地将学生引入新的问题情景.

问题（1）虽然基础，但为考生解答问题（2）中关于粒子在y轴方向的振幅Ay做了方向和方法上的铺垫和暗示（联系h与Ay，确定初、末状态和选取研究过程.），体现了命题者降低试题整体难度的考虑.

在问题（2）的第1）小题中，命题者给考生设置了较隐蔽的“陷阱”：s＝v0T.但稍作分析会发现：初速度大小不同的粒子虽然运动轨迹不同，但具有相同的空间周期性.既然s是反映相同空间周期性的物理量，那么，它就应与初速度v0无关，显然s＝v0T是错误的.

接下来怎么思考？再次审视上述条件发现，除了指出“相同空间周期性”，还指出了粒子运动轨迹不同的原因：初速度大小不同.那么初速度大小是如何影响运动轨迹的呢？比较一下粒子刚射入时洛伦兹力和电场力的大小，结果就不难发现.

若v0＞，粒子的轨迹在x轴上方，且v0越大，轨迹越凸；

若v0＜，粒子的轨迹在x轴下方，且v0越小，轨迹越凹；

若v0＝，粒子沿x轴匀速运动.

隐含条件终于浮出水面：初速度v＝的粒子0的空间周期性就是所有粒子的空间周期性.

可见，试题既考查了学生对物理现象的观察、分析和判断能力，同时也渗透了“共性与个性、普遍与特殊”的物理哲学思想.有了这种思想，学生收获的不仅是试题的正确答案，即便走出考场，走进社会，还将终生受益.因此，试题体现出现代物理教育的社会责任感，彰显出物理学科的品位.

1.3 立意高远 引领问题探究

试题通过展示带电粒子运动的图景，营造了浓厚的探究氛围.如果说问题（1）是引领考生开始探究，或者说是探究的起点，再经过问题（2）第1）小题的初步探究，那么，问题（2）的第2）小题关于A的计算则达到了探究的高潮.

前文提到问题（1）为考生解答Ay做了方向和方法上的铺垫和暗示.在

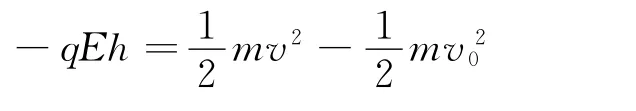
中，当h取最大值时，则h＝2Ay，v即为粒子在轨迹最高点处的速度（方向沿x轴）.如果还能建立粒子在轨迹最高点处的速度v与起始点的速度v0之间的联系，就能顺利解出Ay.这样，问题就转化为对v与v0间关系的探究，而正确找到两者的关系则是解决问题的关键.试题给出的关键性条件“粒子在y轴方向上做简谐运动”为考生指明了思考的方向：在简谐运动的最高点处和最低点处寻找“共性”.于是，简谐运动的对称性自然进入考生的视野，粒子在最高点处和最低点处的加速度或所受回复力等大反向……峰回路转，豁然开朗.至于试题最后要求写出y（t）的函数表达式，那只不过是对探究成果的具体展示而已，自然水到渠成.

不仅如此.学生在体验了探究的艰辛，收获了探究的成果后，更多的可能是对试题本身所展示的物理图景和提供的诸多结论充满质疑：粒子的运动轨迹真是这样的吗？为什么具有空间周期性？粒子在x轴方向的运动又是怎样的？粒子的运动图景与圆周运动、“类平抛”运动之间有联系吗？这些生成性问题诱使优秀学生萌生了新的探究欲望.播洒一种行为，收获一种习惯.当探究成为一种习惯时，实践能力和创新精神的养成，科学素养的提升以及课程目标的达成指日可待.

可见，试题不仅关注学生的现在，还着眼于学生的未来，立意高远深刻.将新课程的三维目标有机融合，全面而深刻地考查学生，不仅体现了命题者本身的创新意识和进取精神，更为重要的是，还体现了命题者对新课改的关注、对学生成长的关注、对民族未来的关注.

2 试题的拓展分析

2.1 粒子的运动方程和运动性质

粒子运动到P点时，其受力和运动情况如图2所示，图中vx，vy和Fx，Fy分别表示粒子的速度和所受洛伦兹力在x轴和y轴方向上的投影，其中

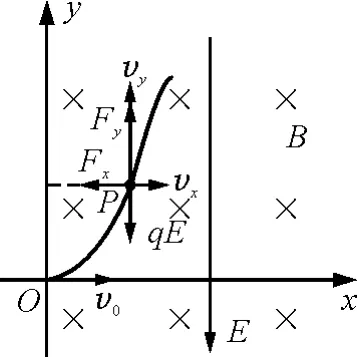
图2

根据牛顿第二定律，在x轴方向有

在y轴方向有

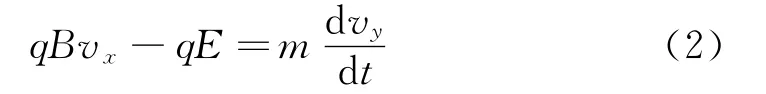
做适当运算，得二阶微分方程

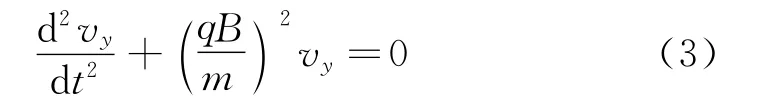
方程的通解为

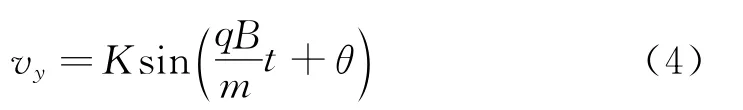
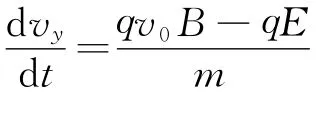
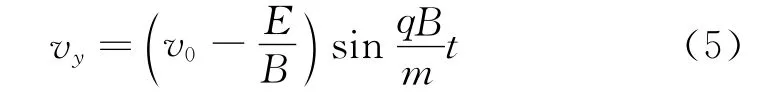
由（2）、（5）式得

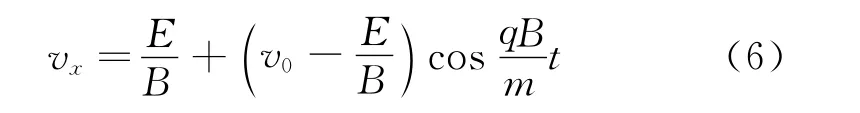
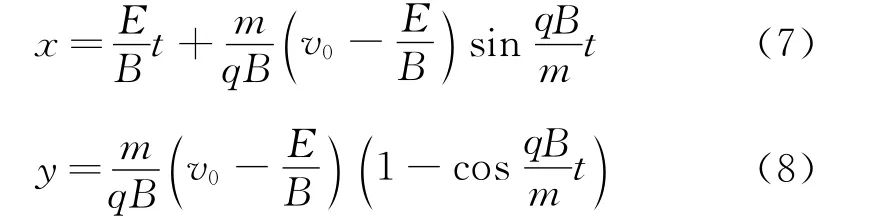
式（5）、（8）表明，粒子在y轴方向做简谐运动.

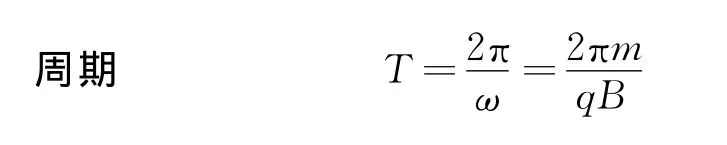
式（6）、（7）表明，粒子在x轴方向的运动是速度为u0＝的匀速运动和振幅、周期的简谐运动的合成.

2.2 粒子的运动轨迹

2.2.1 粒子运动轨迹的空间周期性

当t＝nT（n∈N），则

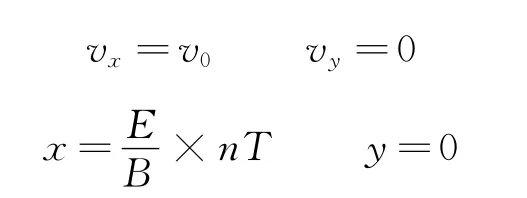
上述计算表明，粒子射入后，每经过一个周期T，粒子就回落到x轴上，速度为v0，但沿x轴正方向前进了s.换言之，只要将粒子在前一个周期的轨迹沿x轴正方向平移s，就得到了它在后一周期的运动轨迹.因此，s反映了粒子运动的空间周期性.

2.2.2 粒子在轨迹最高点和最低点的速度特征

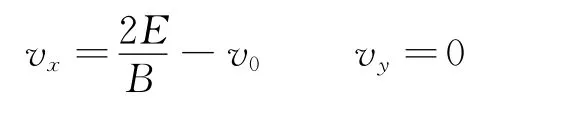
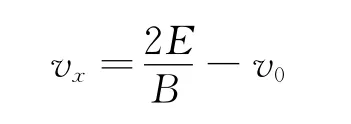
需要指出的是，在轨迹最高点，若＜v0＜，粒子沿x轴正方向运动；若v0＝，v x＝0；若v0＞，粒子沿x轴负方向运动.

2.2.3 粒子的运动轨迹

可以借助计算机描画出粒子的轨迹，只是需要给出有关具体数据.

以质子为例，其质量和电荷量分别为m＝1.67×10－27kg，q＝1.60×10－19C.设电场强度E＝1.67×104V／m，磁感应强度B＝1.67×10－2T，可计算出

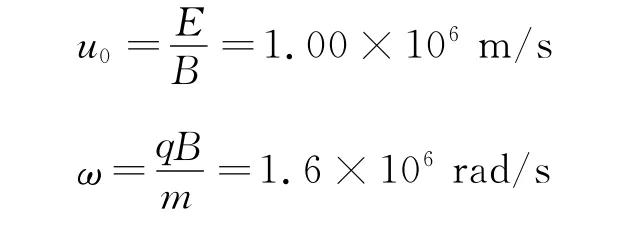
将u0和ω的值代入（7）、（8）式，得到关于t的参数方程（各物理量单位均为国际单位）

图3为几何画板界面，图中描画的8条轨迹与其对应的v0值见表1.

表1 轨迹对应数据

粒子运动的空间周期性在图3中得到了生动再现.试题没有给出类似图中h那样具有“回旋”性质的轨迹，这是命题者为避免因图像过于复杂，影响学生答题而有意为之，但这样的轨迹是真实存在的.

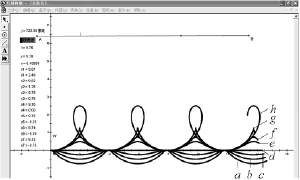
图3

可见，u0＝是决定粒子运动空间的临界速度，2u0＝是决定粒子运动的轨迹是否“回旋”的临界速度.因此，初速度的大小除了影响简谐运动的振幅，还决定粒子运动的空间范围.

3 Ay与s的另类解法

3.1 求Ay

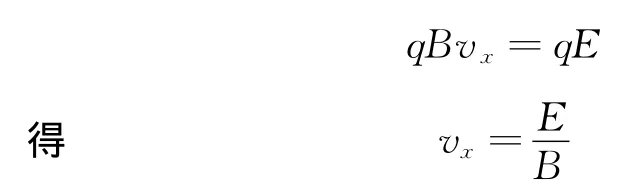
在x轴方向，根据动量定理有

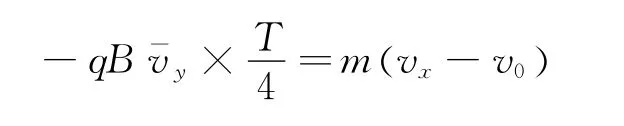
式中表示粒子在内沿y轴方向的平均速度，又

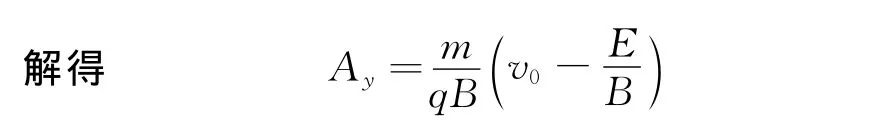
3.2 求s

粒子从射入直至第一次运动到在轨迹最高点，历时，在此过程中，在y轴方向上，根据动量定理有

式中表示粒子在内沿x轴方向的平均速度，而

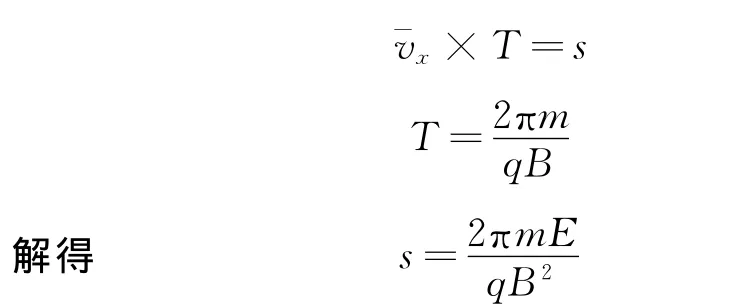
上述关于Ay与s的另类解法，均未超出中学物理范围，学生都可接受，并能运用.解法多元，反映了试题具有一定程度的开放性，这也是经典试题应具有的要素之一.