东露天选煤厂槽仓高边坡稳定性与变形分析

姜海波，宫守才，刘庆雪

(中煤西安设计工程有限责任公司，西安 710054)

1 前言

随着煤矿建设工程的发展，对储煤槽仓的规模和储量要求越来越大，而仓体开挖涉及的边坡稳定性问题也日显重要。平朔东露天选煤厂槽仓位于山西省朔州市，槽仓设计储量为20万 t，服务年限75 a，槽仓平均开挖深度32 m，总坡度71°，为目前亚洲最大规模的储煤槽仓，开挖后边坡的稳定与否直接关系着选煤厂的顺利施工与以后的安全运营，所以，对仓壁边坡开挖、支护前后的变形和稳定性进行深入分析研究非常重要，以便对边坡选择合理、经济的支护措施。

2 场地工程地质条件

平朔东露天煤矿位于朔州市平鲁区，地面标高介于1333．38～1401．01 m 之间，最大地面高差67．63 m，场地地貌单元属黄土梁，场地地表土层主要有:

①填土(Q2al4):属淤积坝后堆积的新近堆积土层，呈可塑—软塑状态，具高压缩性，极不均匀。

②黄土状粉土(Q2del4):属滑坡堆积物，新近堆积土层，坚硬。

③黄土(Qeol3):为场地地表主要堆积物，浅黄色，土质均匀，坚硬—硬塑状态，中压缩性，湿陷性中等—强烈。

④黄土(Qeol3):褐黄色，土质均匀，呈坚硬—硬塑状态，中压缩性，不具湿陷性。

④－1黄土(Qeol3):褐黄色，土质均匀，呈可塑—软塑—流塑状态，中压缩性，不具湿陷性。

④－1－1黄土(Qeol3):土质均匀，可塑—软塑—流塑状态，中压缩性，不具湿陷性。层厚0．50～4．50 m，不连续，呈透镜体分布在部分孔中。

⑤黄土(Qeol2):棕红色，菱块状结构，可见高角度的裂隙，裂隙中充填砂粒，呈硬塑—坚硬状态，中等偏低压缩性。

⑥粉质粘土(Qel+pl1):浅棕红、棕黄色，块状结构，呈硬塑—坚硬状态，中等偏低压缩性。

⑦强风化泥岩 (P1x):灰色—黄灰色，泥质胶结，具薄层水平层理，岩芯呈碎块状，遇水崩解，塑性较强。

⑦－1强风化砂岩 (P1x):灰色—黄灰色，泥质胶结，具薄层水平层理，岩质疏松，裂隙发育，岩芯呈块状—碎块状。

场地在勘察期间有地下水分布，地下水埋深介于1331．08 ～1344．28 m，属上层滞水，受相对隔水层分布影响，水位标高变化大，主要受大气降水补给，季节变化明显。在冲沟沟底或下游排出。沟谷底现湿地或下降泉出露。

3 槽仓边坡基本特征

槽 仓 长 237．0 m，上 口 宽 40．0 m，下 口 宽16．0 m，深 24．5 m，仓壁坡度为 60 °，槽底布置有高6．30 m，宽16．0 m的输煤暗道，暗道上部布置有3个落煤筒，槽仓纵断面图和横断面图见图1和图2。文章重点对仓壁及暗道边坡稳定性进行分析计算。仓壁边坡斜壁段高21．8～25 m，直壁段高6．3 m，最大总高度31．3 m，边坡安全等级为一级。槽仓建成后，坡面作为仓壁承受煤压，存在空仓和满仓交替的两种工况，对变形要求非常高。暗道土层为④－1和④－1－1，其中④－1－1层黄土为高灵敏饱和黄土，触变性强，一经扰动，呈流塑状态，在暗道直壁范围内有不连续地下水位，这些因素都对边坡稳定性造成了不利影响。

图1 槽仓纵断面图Fig．1 Longitudinal profile of bunker

图2 槽仓横断面图Fig．2 Cross-sectional drawing of bunker

4 边坡稳定性评价与变形分析

边坡岩土体稳定性的分析计算，是边坡勘察设计的核心问题，目前仍以极限平衡法为主。文章先采用极限平衡理论对开挖边坡分未支护和支护后两种状况进行计算，该理论按照斯宾塞法、摩根斯坦(Morgenstern)－普赖斯(Price)法、毕肖普法和简布法分别计算出4种安全系数，再采用有限元方法计算边坡的变形特征。该方法应用弹塑性理论，避免了极限平衡分析法中将滑体视为刚体而简化为刚体的缺点，可近似的根据应力、应变规律去分析边坡的变形、破坏机制［1］，以验证加固方案的有效性［2～4］。

4．1 计算模型及参数选取

采用极限平衡法进行分析，开挖模型如图3所示，地层取近似水平地层，模型长85 m，高52 m。边界条件为:设定模型的上部和右侧为自由边界，左侧为水平约束，底面边界采用固定约束，其他边界设定为位移自由边界。土体按弹塑性考虑，采用摩尔－库仑屈服准则进行模拟。

组成边坡岩土体的物理力学指标是边坡稳定分析和综合评价的重要基础资料和依据。该场地地层较为复杂，故采用直接快剪试验、增湿直剪试验、饱和直剪试验和残余剪切试验，获取土体不同状态下的力学参数，力求计算参数接近真实情况。

1)直剪试验(快剪)。考虑槽仓开挖及仓体边坡设计，对场地上部地基土进行了直剪(快剪)试验，试验结果见表1。

表1 地基土直剪试验(快剪)结果统计表Table 1 Statistic result of straight scissors test

2)增湿直剪试验及饱和直剪试验。依据经验，考虑到槽仓在建成后使用过程中地基土的含水率普遍会有所增高，因而对场地内的③、④层非饱和黄土进行了增湿直剪试验及饱和直剪试验，增湿时含水率一次增至液限含水率后进行直剪，增湿直剪试验统计结果见表2，饱和直剪试验统计结果见表3。

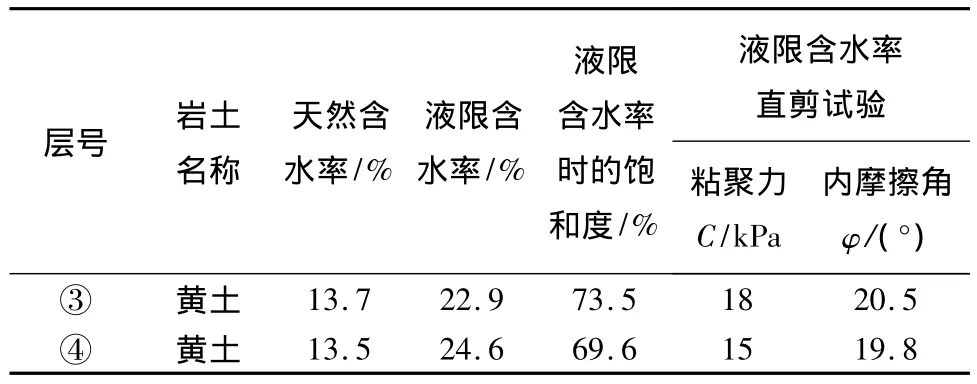
表2 地基土增湿直剪试验(快剪)结果统计表Table 2 Statistic result of straight scissors test with different percent moisture content

表3 地基土饱和直剪试验结果统计表Table 3 Statistic result of straight scissors test of saturated soil

3)残余剪切试验。针对产品槽仓边坡土层的特性，即在粘性土中，坚硬的粘性土应力－剪应变曲线常呈现较大峰值，超越峰值后，当剪应变相当大时，抗剪强度不再变化。对产品槽仓边坡的③、④、④－1层黄土进行残余抗剪强度试验，残余抗剪强度试验统计结果见表4。

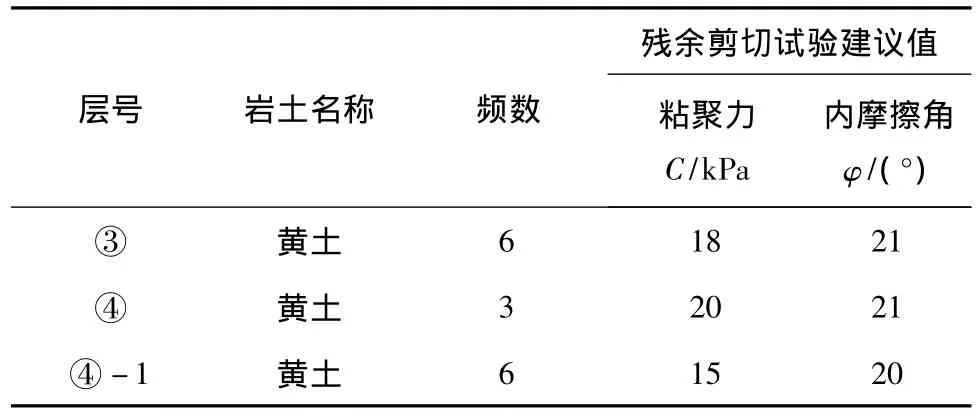
表4 地基土残余剪切试验结果统计表Table 4 Statistic result of residual scissors test

分析以上试验数据，由增湿直剪试验及天然土的直剪试验对比可以看出，含水率对粘性土的粘聚力C值有较大影响，随着含水率的增大，粘聚力C呈减小趋势，内摩擦角虽呈递减趋势，但变化不如粘聚力明显。将各试验结果对比分析，在原数据上进行适当增减，作为计算式的数据，地下水位附近及以下土层按饱和土层考虑，以饱水指标作为计算参数，各层土的计算参数取值见表5。

表5 各层土的计算参数取值Table 5 Chart for computing parameter of each layer soil

4．2 边坡支护前稳定性与变形评价

选取槽仓一典型剖面为例，考虑槽仓开挖后在天然条件下、降雨条件下、地震条件下及降雨与地震联合作用条件下的边坡稳定性问题。图3为开挖槽仓支护前的数值计算模型，图4和图5为支护前应力和位移分布图。

天然状况下，未支护的边坡仅考虑边坡岩土体的自重作用，计算时采用天然状态下的粘聚力、内摩擦角及天然容重，边坡的稳定性系数为0．6左右，为不稳定状态，需要进行边坡开挖支护，以确保槽仓边坡安全运营。降水状况下，据气象资料，日最大降水量选取153 mm，连续最长降水时间为13 d，边坡稳定性系数较天然状态降低约9．8% ～13%，对边坡的开挖支护要考虑降雨的影响。地震状况下，考虑边坡在7度地震作用下，边坡稳定性下降了19．7%～22%，可见地震对边坡稳定性有显著影响。在最差的工况下即遇到地震与暴雨联合作用时，稳定系数降低约22．3% ～28．5%，该状态较地震状态稳定性下降了10．8%，可见地震对边坡的影响是最大的，也是最显著的。

图3 槽仓支护前数值计算模型Fig．3 Numerical calculation model of unreinforced bunker

图4 槽仓支护前应力分布图Fig．4 Stress envelope graph of unreinforced bunker

图5 槽仓支护前位移分布图Fig．5 Displacement graph of unreinforced bunker

可见，槽仓开挖若不采取任何支护措施，该边坡将无法存在，因此，槽仓边坡必须边开挖边加固，才能达到安全使用的稳定性要求。由槽仓支护前应力图可以看出，槽仓斜壁与直壁转角处和仓底坡脚处也是变形最大的地方，此处是边坡加固的重点部位。从支护前位移分布图来看，边坡破坏面为圆弧滑面，加固时支护结构一定要穿过滑面一定深度，才能保证边坡斜壁部分的稳定性。

表6 边坡支护前不同工况下稳定性计算表Table 6 Stability calculation before reinforcement of different conditions

4．3 边坡支护后的稳定性与变形分析

4．3．1 支护后边坡稳定性分析

针对槽仓开挖未支护的稳定性与变形情况，设计采用多种方法联合支护方案，设计支护图如图6所示，采用边开挖边支护的施工方法。边坡斜壁段采用土钉墙复合支护结构，土钉支护是通过以增加边坡自身稳定性的主动制约机制为基础的复合土体，不仅有效地提高了土体整体刚度，弥补了土体抗剪、抗拉强度低的弱点，通过相互作用，土体自身结构强度的潜力充分发挥，并且改善了边坡变形和破坏性状，显著提高了整体稳定性。但是土钉支护水平位移偏大［5］，而槽仓结构本身对位移有较高的要求，故将双数排号的土钉改为锚杆，施加200～250 kN的预应力，并在锚杆锚头部分设置宽400 mm、厚250 mm的横向钢筋混凝土梁，以减小水平位移量，加强面层的整体性。锚杆倾角15°，长30～35 m;土钉倾角15°，长27 m，锚杆与土钉隔排设置，垂直间距1．1 m，水平间距1 m;槽仓直壁段采用双排灌注桩和钢内撑复合结构支护，尽量避免扰动暗道侧壁土体。外侧支护桩直径1 m、间距1．47 m，主要承受侧壁土压力，内侧暗道桩直径1．5 m、间距1．72 m，既承受侧向土压力，又承受上部结构传来的荷载，为混合型受力桩。直壁段边坡采用逆作法施工，即先施工钢内撑和暗道顶板，再挖去暗道内土体，以确保边坡稳定性。

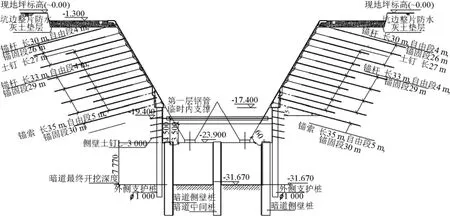
图6 槽仓边坡支护结构图Fig．6 Picture of the reinforced slope

表7 边坡支护后各种工况下的稳定性系数表Table 7 Stability calculation after reinforcement of different conditions

边坡支护后的稳定性分析分4种工况进行计算，各种工况下稳定性系数见表4。槽仓开挖支护后天然状态下稳定性系数可以达到1．30以上，可以满足该工程的稳定性要求。该支护方式在降雨条件下可以达到1．20以上，地震条件下稳定性系数约为1．08，基本处于极限平衡状态，在降雨与地震联合作用下，稳定性系数与降雨条件下相差不大，可见几种工况下最低稳定系数为1．05，边坡处于极限稳定状态，可达到工程安全运营的要求。

4．3．2 支护后边坡变形分析

采用有限元对槽仓边坡加固支护情况进行数值分析，结果如图7～图10所示。

可以看出，边坡加固后边坡处无应力集中区域，加固前的应力由加固措施承担，大大提高了边坡稳定性。边坡加固前边坡位移达到1．4 m，加固后边坡水平最大位移不足5 cm，考虑有限元计算精度，此变形大小满足要求。最大竖向位移13 cm，在暗道底板处，主要是由于模拟时未考虑暗道底板的硬化引起，对仓壁边坡变形计算不影响。加固前边坡存在明显的圆弧形滑面，加固后总位移分布已不存在滑面，变形在允许范围之内。可见，该支护方案非常适合该边坡。

图7 槽仓支护后应力分布图Fig．7 Stress envelope picture of reinforced bunker

图8 槽仓支护后总位移分布图Fig．8 Displacement picture of reinforced bunker

图9 槽仓支护后水平位移分布图Fig．9 Horizontal displacement picture of reinforced bunker

5 结语

针对东露天槽仓高边坡，利用极限平衡法和有限元法对边坡支护前后在不同工况条件下的稳定性进行了计算，分析了边坡支护前后的应力与变形分布，得出以下结论:

1)槽仓边坡支护前无法达到使用要求，斜壁与直壁转角处和仓底坡脚处为应力集中和变形最大处，是加固的重点部位。

2)边坡采用土钉墙复合结构和灌注桩+钢内撑复合结构等多种支护后，天然工况稳定系数达到1．3以上，地震+饱和工况下稳定系数1．05，边坡处于极限稳定状态，边坡满足使用要求。

图10 槽仓支护后竖向位移分布图Fig．10 Vertical displacement picture of reinforced bunker

3)边坡加固后应力集中带消除，位移满足使用要求，加固前的滑面也已不存在，该支护方案非常适合该边坡。

［1］王 军．高陡岩土边坡有限元分析及综合治理［D］．长沙:中南大学，2005．

［2］王国体，王碗娣．土坡稳定分析应力状态新方法的过程解析［J］．中国工程科学，2010，12(1):52 － 55．

［3］王靖涛．论岩土塑性体应变与剪应变的相互作用原理［J］．中国工程科学，2006，8(9):24 －29．

［4］郑颖人，赵尚毅，邓楚键，等．有限元极限分析法发展及其在岩土工程中的应用［J］．中国工程科学，2006，8(12):39－61．

［5］程良奎，李象范．岩土锚固、土钉、喷射混凝土——原理、设计与应用［M］．北京:中国建筑工业出版社，2008．