基于高精基准的面对面垂直度评定与软件开发

林翔

（福建商业高等专科学校，福建福州350012）

1 垂直度评定的核心问题

按国标《GB/T 1958-2004》[1]规定，面对面垂直度误差属于位置公差中的定向误差范畴，指实际被测平面要素相对于给定基准平面在垂直方向上的变动量，此变动量要符合“最小条件”原则，即将被测平面上的测点投影于基准平面，求取这些投影点的二维直线度误差，此即为被测平面相对于给定基准平面的垂直度误差值。

如果基准平面是已知的，即其平面方程（可记为π0∶a0x+b0y+c0z+d0=0的法矢T=(a0,b0,c0)已给出，从文献[1]中关于被测平面对于基准平面垂直度误差的概念描述可知，只要把被测平面上各点投影到基准平面，则求垂直度误差实际上就是求全体投影点的二维直线度误差，如此则空间问题就转化为二维的问题；如果基准平面要素是通过测量获得的（设基准上测量点集为P={Pk(xk,yk,zk),k=1,…,n}），毫无疑问要以测量点为依据拟合出平面作为基准平面π0，然后进行垂直度误差评定。按照文献[1]规定，拟合平面π0必须是通过平面度误差计算过程而获得的，才可以作为基准平面，进一步在π0的基础上继续进行面对面垂直度误差计算。

显然，问题的核心是如何求得符合“最小条件”的基准平面，只有在拟合出高精度基准平面的基础上，才有可能求取高精度的面对面垂直度误差。为此，业界专家们推出了不同的平面拟合方法：文献[2-3]提出以“最小二乘平面”法求取基准平面，虽然合乎文献[1]规定但计算精度有局限；文献[4]用“直接比较法”与“坐标法”求取，对狭长平面之类的特殊情况用“光轴法”、“水平仪法”求取，方法简便易行但精度不高；文献[5]也有类似的情况。本文针对求取基准这一核心问题提出新算法，使基准平面的求取过程与垂直度误差评定过程均符合“最小条件”的原则，从而得到高精度的面对面垂直度误差值。

2 基准平面拟合

设基准平面上测量得到的点集P={pk(xk,yk,zk),k=1～n}，拟合平面π0的法向量为T=(a0,b0,c0)，如图1。由文献[1]规定可知，要使π0符合“最小条件”成为最佳拟合基准，π0的平面度误差值计算过程必须要满足“最小区域”原则，即须求得一对平行的平面包容点集P，且令两平面间距离达到最小。

求最佳拟合基准的总体思路是：首先以“最小二乘法”求取初始拟合平面，进而将拟合平面的平面度误差计算向“最小区域”靠近，令结果满足“最小条件”。记由“最小二乘法”得到的初始拟合平面方程为π0（求取的算法与过程在文献[2-3]中均有叙述，此不重述），初始平面度误差为δ。经过观察分析，发现可以通过有意识地细微转动π0（即转动π0的法方向），使δ值降下来。

设Pk(xk,yk,zk)至初始基准平面 π0距离为 δk，δi，δj分别为{δk,(k=1,…,n)}之最大值与最小值，相应点为 Pi，Pj，即 δi=max(δk),(k=1,…,n)；δj=min(δk)，(k=1,…,n)。

记初始平面度误差 δ=δi+δj=max(δk)+min(δk)(k=1,…,n))；Ai，Aj为 Pi，Pj在 π0的投影点，从 Ai点沿AiPi距离ε处取 Ai′点（ε是一很小的值），从 Aj点沿 AjPj距ε处取 Aj′，Ai′Aj′中点记为 S ，于 π0上取点 S′，令S′S ⊥ Ai′Aj′。

以 Ai′,Aj′,S′3个点作平面 π0′，π0与 π0′之间夹角甚小，可视 π0′为 π0绕 S′S 做微小转动而获得；从平面方程特点视之，π0′是以π0之法向量T=(a0,b0,c0)作微小转动后生成的。

Pi,Pj,Ai′,Aj′四点共面，记为 π1，π0经 π1剖切成如图2所示，易见 Pi至 π0′之距 δi′＜ δi，Pj至 π0′之距为 δj′＜δj，即有 δi′+δj′＜ δi+δj，亦即当 π0经微小转动生成 π0′后有可能把 δ值降下来，这正是拙文之总体思路所期盼的第一个结果。

究竟能否成功地将π0转动生成π0′而令δ降下来，还需要计算点集P对π0′的平面度值δ′，与原平面度值δ进行比较以便判断。比较的结果不外乎以下3种情况：

1）若 δ′＜δ，π0′取代 π0，对新 π0重复上述的微小扰动，重复计算、判断过程；

2）若 δ′≥δ，则缩小ε并重新计算出 π0′及 δ0′，判断是否 δ′＜δ；

3）若ε经多次缩小而成为非常小的值，已达到精度要求，则计算终止，此时δ就是符合“最小区域”要求的平面度误差值，π0即所求的最佳拟合基准平面。

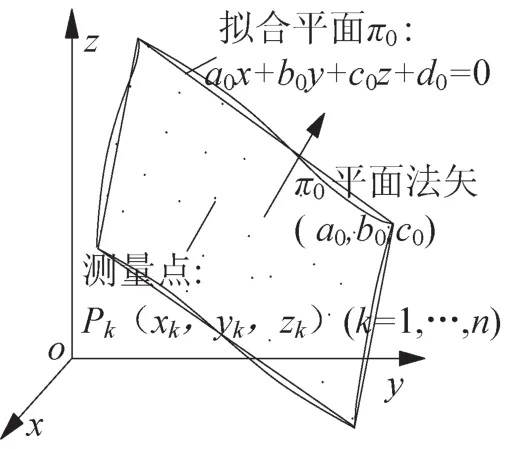
图1 基准平面拟合示意图Fig.1 Fitting of the datum plane

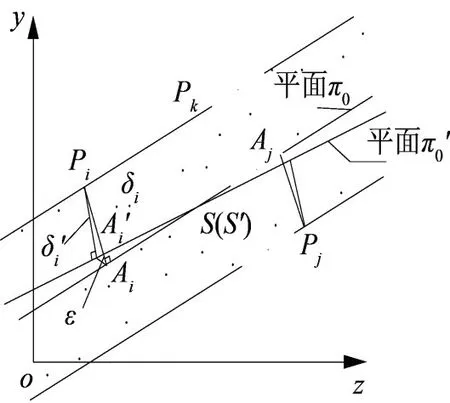
图2 点集P与平面π0，π0′关系图Fig.2 SetP&plane π0and π0′

3 算法论证

对于上述结论的“最小条件”符合性作简要论证。如图2，Ai，Ai′分别为Pi在π0，π0′的投影，在ΔPiAiAi′中∠PiAi′Ai为钝角，因钝角之对应边必定小于任一邻边，故 Ai′Pi＜AiPi；同样，记 Aj，Aj′为 Pj在π0，π0′的投影，∠PjAj′Aj亦为钝角，亦成立 Aj′Pj＜AjPj。综之有 Ai′Pi+Aj′Pj＜AiPi+AjPj，即δ′＜ δ。这表明由于π0微小转动得到π0′后，点集P对于π0′的平面度误差降下来了，且是单调下降，这也说明此平面度误差的计算过程是收敛的，不断趋于“最小区域”。

本文取用了数十例平面度误差算例对上述算法进行验证，计算结果表明本文算法的精度均达到或超过原文，进一步证明本算法的“最小条件”符合性。现摘取4例列于表1予以说明。

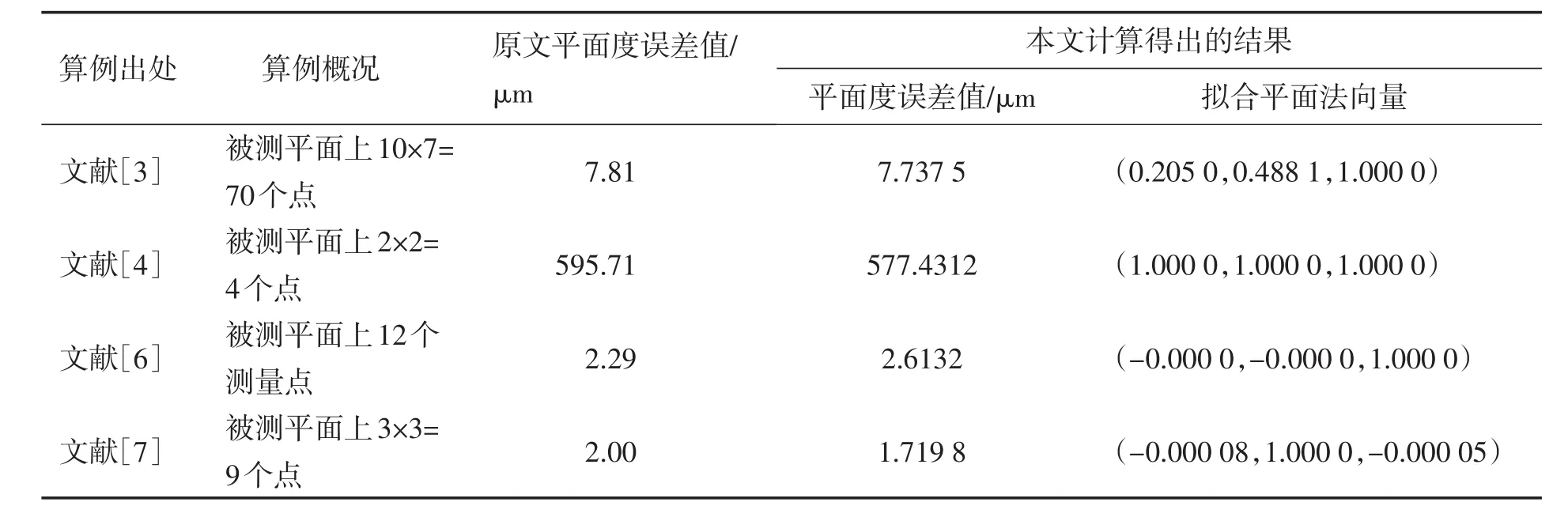
表1 平面拟合算例结果比较Tab.1 Result comparisons of flat-to-flat fitting calculation

4 垂直度评定

4.1 面对面垂直度误差算法

上述获得高精度的拟合基准平面为高精度评定面对面垂直度误差打下好的基础。对三维坐标系旋转，使xoy面与基准平面重合，被测平面上测量点在基准平面的投影可视为二维平面点，记为Q={Qk(xk,yk),k=1～m}，解读文献[1]之规定，显然求垂直度误差就可转化成为求点集Q的二维直线度误差。

设Q的基准直线为l0，与之平行的两条直线为l1，l2，把Q夹紧在其间，并使得l1，l2间距 f达到最小，如图3所示，f即为点集Q的二维直线度误差，亦即面对面垂直度误差值。

1）通过“最小二乘法”求得基准直线l0（设斜率为k0、截距为b0，方程：y=k0x+b0），此时的 f值为初始直线度误差，f=f1+f2。

2）在此基础上细微改变k0值，即对l0进行细微的转动，目的是把 f值降下来。设点集Q中距l0的最大、最小值为 f1，f2，所对应的点分别为 Qi，Qj，Qi，Qj在 l0的投影点为 Qi′，Qj′，在 QiQi′方向上距 Qi′距离 ξ处取 Qi′点（ ξ是很小值），同样在 QjQj′方向上距 Qj′距离ξ处取 Qj′点，即 Qj′Qj′=Qi′Qi′= ξ。以 Qi′，Qj′作直线 l0′，易见 Qi到 l0′之距离小于Qi到 l0距离，Qj到 l0′之距离也小于Qj到 l0距离，这表明 l0′有可能把 f值降下来。

到底能否把 f降下来，该文是通过点集Q对于l0算出新的直线度 f′，与之′前的 f比较进行判断：1）若 f′＜f，l0取代 l0；

2）若 f′≥f，则缩小 ξ，以 ξ值重新求出直线l0′，再计算直线度 f′，观察 f 值下降与否；

3）若ξ不断缩小已能满足精度要求，计算终止，最后得到的直线度误差 f，即为垂直度误差值。

图3 投影点集Q与基准l0示意图Fig.3 Diagram of projection point set Q&l0benchmark

4.2 垂直度算法流程图

按照上述的面对面垂直度误差算法过程，依软件开发要求作出算法流程图如图4所示。本算法程序用C语言编制。（程序代码略）

图4 垂直度算法流程图Fig.4 Diagram of perpendicularity algorithm

4.3 算例测试

选用3个典型算例对程序加以测试，并把比较结果列于表2，对本文算法与软件的正确性可靠性略作说明。

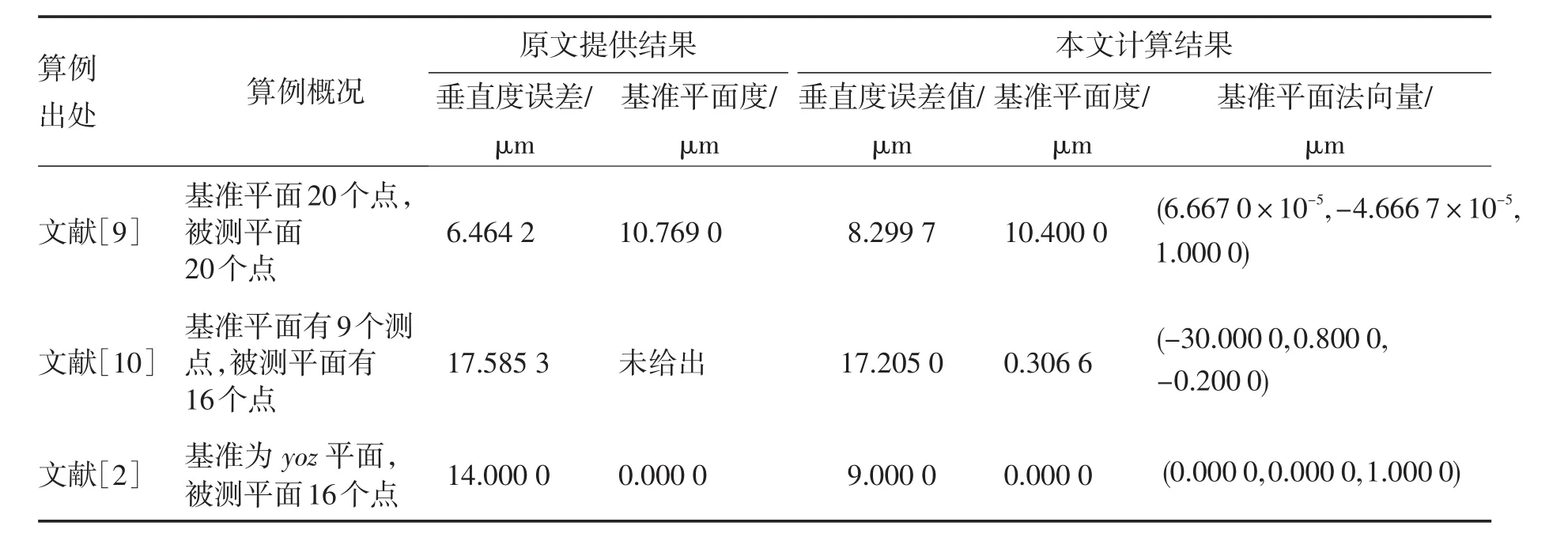
表2 面对面垂直度误差算例计算结果比较Tab.2 Test calculation comparisons of flat-to-flat perpendicularity error

5 结束语

面对面垂直度误差评定的关键在于基准平面的确定，核心问题是基准平面的平面度误差计算，难点在于此计算必须符合“最小条件”。本文从国标规定出发，从理论上解决了平面度误差的高精度计算问题，从而解决了拟合基准平面在“最小条件”方面的符合性；通过算例验算与结果比较，表明此理论与算法都是正确可行的。在高精度基准的基础上，引用文献[7]所提供的成熟算法，求出高精度的面对面垂直度误差，也就水到渠成了。

本文引用的算例有限，欢迎同行专家对拙作及相应软件批评指正。

[1]中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.GB/T 1958-2004产品几何量技术规范（GPS）形状和位置公差检测规定）[S].北京：中国标准出版社，2004.

[2]甘永立.形状和位置误差检测[M].北京：国防工业出版社，1995：137.

[3]崔长彩，车仁生，罗小川，等.基于实数编码遗传算法的平面度评定[J].光学精密工程，2002，10（1）：36-40.

[4]杨伟敏.PC_DMIS软件平面度误差评定方法研究[J].工业计量，2012，22（3）：14-15.

[5]王少锋，许玉德，周宇，等.基于临界平面法的钢轨裂纹萌生寿命预测模型研究[J].华东交通大学学报，2011，28（5）：77-82.

[6]倪爱晶，郑联语.基于形状误差不确定度的大尺寸测量系统优化配置方法[J].计量学报，2011，32（4）：289-295.

[7]王冉.零件尺寸在线检测系统的开发及误差计算方法研究[D].南京：南京航空航天大学，2000：57-58.

[8]林翔.直线度误差的新算法及其在微机上的实现[J].计量技术，2007（8）：19-21.

[9]刘平.用计算机评定平面对平面的垂直度误差[J].宇航计测技术，1989（4）：22-30.

[10]杨金霞.基于坐标测量数据的位置误差评定软件包的开发[D].西安：西安理工大学，2008：42-43.