三容液位过程的内模控制应用研究

崔海全，赵志诚

(太原科技大学电子信息工程学院，山西太原 030024)

0 引言

液位作为工业控制中的重要参数之一，在食品加工、石油化工、冶金、能源等工业生产领域中都有涉及，因此液位是过程控制领域中非常普遍的一种被控过程［1-2］。由于液体没有确定的形状，易受设备等周围环境的影响，使液位过程通常具有时滞、非线性和时变等特性，采用常规控制方法难以满足高性能的控制要求，为此常采用基于过程模型的先进过程控制策略。然而，在实验研究和工程应用中，由于被控过程数学模型的阶数往往较高，且结构复杂，直接进行控制器的设计相对困难，因此对模型降阶方法的研究显得尤为重要，采用降阶方法可以为控制系统的设计带来极大的方便［3-4］。

“过程控制系统”课程教学中只给出了单容和双容液位过程数学模型参数的阶跃响应曲线法［5］，而对于三容液位过程数学模型的参数辨识，则没有直接的实验方法。本文将三容液位过程看作两个单容流量过程和一个单容液位过程的串联，利用机理分析和实验辨识相结合的方法，建立三容液位过程的数学模型。为方便控制器设计，根据模型降阶原理，使用多种降阶方法对高阶数学模型进行了降阶处理，最终获得基于次最优拟合法的一阶加时滞模型，所得的降价模型能较准确的反映三容液位过程的静态和动态特性，并对其进行了输入干扰开环响应特性分析。最后，根据内模控制原理设计了一种液位过程控制器，进行了三容液位过程控制实验，结果表明本文的研究与设计方法具有一定的有效性。

1 三容液位过程建模

三容液位过程结构如图1所示。

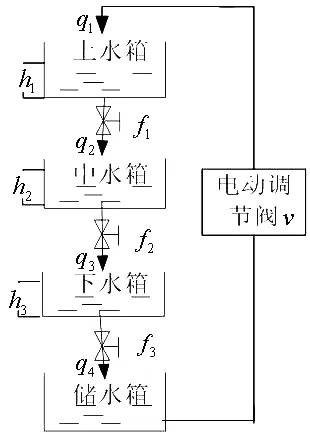
图1 三容液位过程结构

图中上水箱和中水箱直径为25cm，高度为20cm，下水箱直径为35cm，高度为20cm。上水箱液位高度为h1，流入量为q1，流出量为q2。中水箱液位高度为h2，流出量为q3。下水箱液位高度为h3，流出量为q4。f1、f2和f3分别为上、中和下水箱的出口阀开度，v为电动调节阀开度。

1.1 建模方法

过程建模方法主要包括机理分析和实验辨识两种，其中机理分析法能够得到比较准确的模型，且模型中参数意义明确。然而由于实际过程存在的不确定性和众多外界因素干扰，使建立的模型无法准确反映被控过程。实验辨识法从所得的测量数据获得模型，能够得到精确度较高的数学模型，但辨识过程复杂。本文通过机理分析法建立数学模型结构，根据测量数据，利用实验辨识法确定数学模型参数，从而得到液位过程的数学模型。

1.2 建模步骤

文中将三容液位过程过程分解为上、中水箱流量过程和下水箱液位过程的串联，输入量为电动调节阀开度v，输出量为下水箱液位高度h3。将阀门开度与流量之间近似考虑为比例关系，则对于上水箱和下水箱单容液位过程分别有

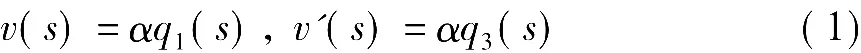
式中，α为比例系数，v(s)和v'(s)分别为上、下水箱单容液位过程的电动调节阀开度，q1和q3分别为上、下水箱单容液位过程的流入量。

三容液位过程数学模型G(s)为

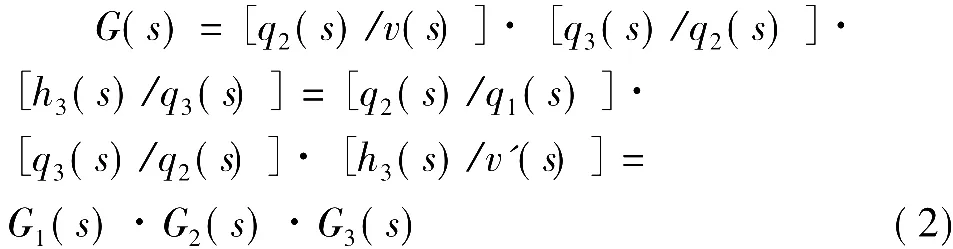
式中，G1(s)和G2(s)分别为上、中水箱单容流量过程数学模型，G3(s)为下水箱单容液位过程数学模型。考虑上水箱，根据动态物料平衡有

式中，A1为上水箱横截面积。采用线性化处理后可近似认为q2的增量部分与h1的增量部分成正比，与出水阀f1的液阻R1成反比，即

将式(4)代入式(3)消去q2，同时考虑上水箱存在的时间延迟，经拉氏变换获得上水箱单容液位过程数学模型为

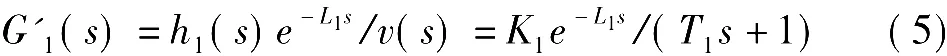
式中，K1=R1/α，T1=A1，R1和 L1分别为数学模型的开环增益、惯性时间常数和延迟时间常数。

通过实验辨识法确定数学模型各参数值。实验使用自主开发的测控软件为VisualStudio2005开发环境下基于C#实现的。将电动调节阀开度v调到一定开度，当液位平稳后将v增加其量程的10%，获得阶跃响应曲线如图2的上水箱液位曲线(虚线曲线)所示。其中，横坐标为运行时间，纵坐标为液位高度。

根据阶跃响应曲线法，获得上水箱液位过程数学模型为

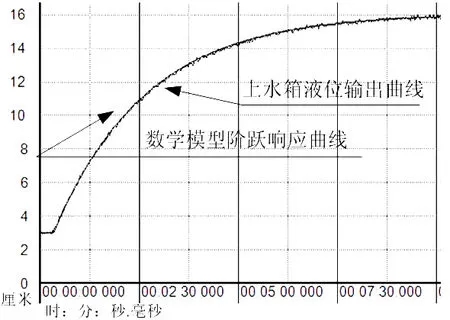
图2 上水箱液位曲线与数学模型阶跃响应曲线

利用C语言编写一阶加时滞模型得到仿真算法程序集并加载到自主开发的测控软件中，输入模型各参数值和阶跃输入值。其中阶跃输入值为电动调节阀量程的10%，可得数学模型的阶跃响应曲线，如图2实线曲线所示。结果可知所得模型输出响应曲线能够很好的逼近实际测量曲线，验证了所建数学模型的精确性。

在上水箱单容液位过程数学模型的基础上，可得其单容流量过程数学模型为

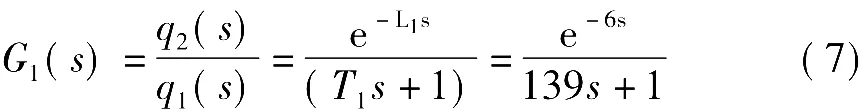
同理，可得中水箱单容流量过程和下水箱单容液位过程的数学模型分别为

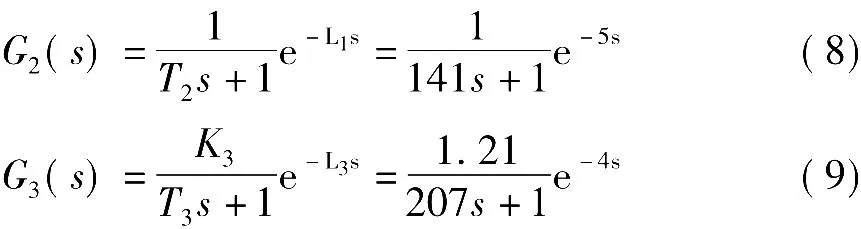
由式(2)可得三容液位过程的数学模型。同时，根据多次获得的实验数据修正三容液位过程的延迟时间常数，可得

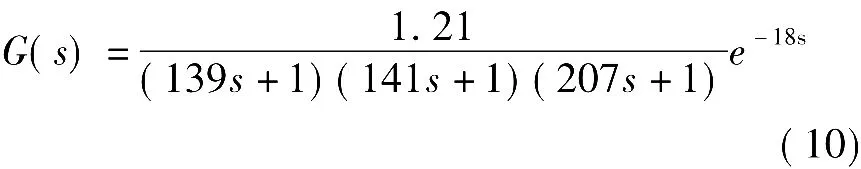
为了验证所建模型的正确性，利用C语言编写三容液位过程数学模型仿真算法程序集并加载到测控软件中，阶跃输入量为电动调节阀开度的10%，获取数学模型阶跃响应曲线(实线)，并与实际输出曲线(虚线)进行比较，结果如图3所示，可见两条曲线几乎完全重合，验证了模型的有效性。

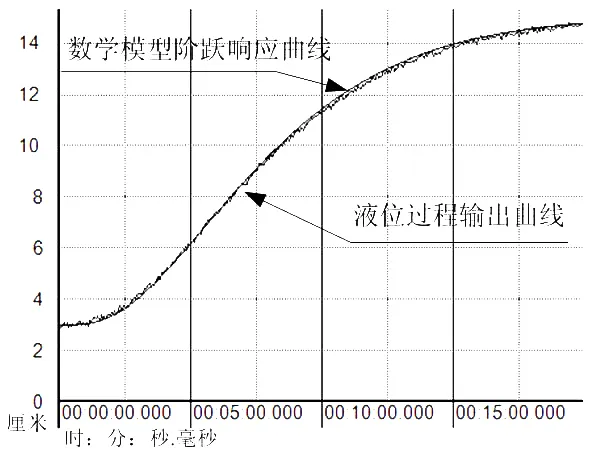
图3 液位过程输出曲线和模型阶跃响应曲线

2 模型降阶

为方便控制器的设计与实现，通常需要对复杂的数学模型进行化简处理。本文采用四种方法，对三容液位过程数学模型进行降阶处理，并通过比较获取拟合效果最佳的一阶加时滞模型。

1)基于传递函数的拟合方法

根据目标传递函数G(s)=Ke－Ls/(Ts+1)，来求G(s)关于s的一阶和二阶导数，可得

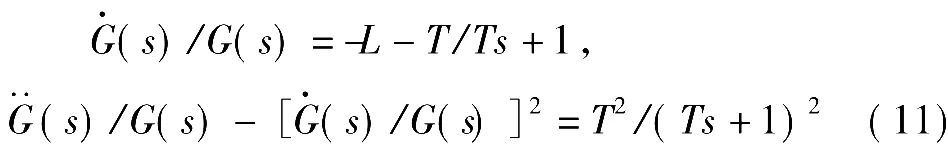
取上式在s=0处的值，可得平均驻留时间为

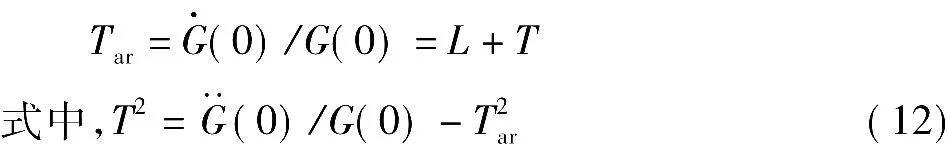
根据 L=Tar－T，K=G(0)，得

基于频域响应的拟合方法。根据一阶加延迟模型，得其频域响应为

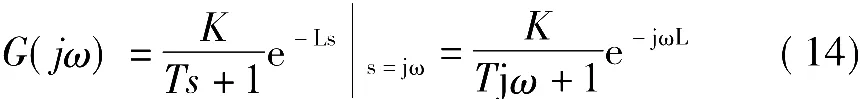
在剪切频率ωc下的极限增益Kc值实际上是Nyquist图与负实轴的第一个交点，它满足的方程组如下:

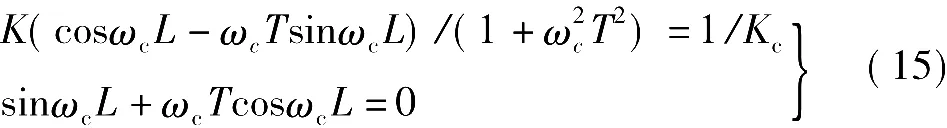
解出L和T，根据K=G(0)，可得

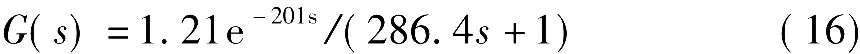
基于最小二乘法的拟合方法。一阶加延迟模型对应的阶跃响应时域解析式为

采用最小二乘拟合方法，由阶跃响应数据拟合出系统的一阶加延迟模型为

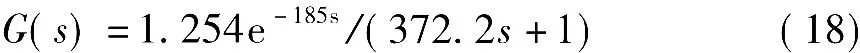
对一阶加延迟模型中的时间延迟项采用Padé近似，将这种延迟系统采用近似的最优化来求解的，称为次最优降阶方法［6］。利用最优算法进行模型降阶思想，将ISE指标作为目标函数，对参数进行寻优，得出目标函数最小的最优降阶模型:

通过Matlab仿真，获得了原始模型和各降阶模型的阶跃响应曲线如图4所示。其中，基于传递函数拟合方法获得的模型拟合效果最差。其中，横坐标为仿真时间，单位为秒，纵坐标为仿真输出结果。

仿真运行至30分钟处，在输入中加入幅值为2，时长为10秒的输入干扰，得其开环响应如图5所示。从拟合结果可以看出，基于次最优降阶方法得出的模型拟合效果优于其他几种方法。

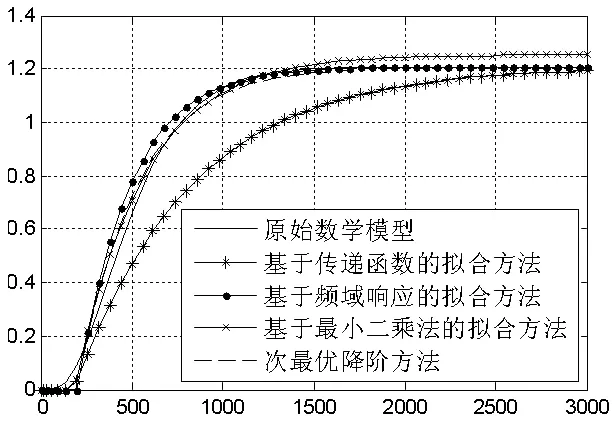
图4 原始模型和各降阶模型阶跃响应

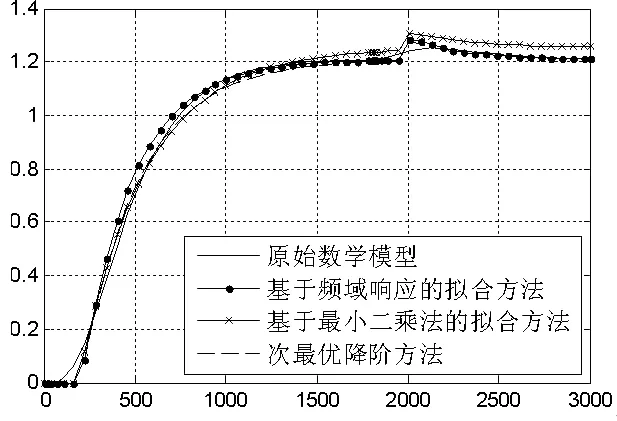
图5 原始模型及各降阶模型的干扰输出

3 内模控制

3.1 控制器设计

内模控制IMC(internal model control)结构图如图6所示。其中，P(s)为被控过程，M(s)为被控过程数学模型，CIMC(s)为内模控制器，d(s)为系统干扰，r(s)、y(s)分别为系统的输入和输出。

图6 IMC结构框图

将图6转换为图7所示的简单反馈控制系统，则反馈控制器为根据内模原理，设计内模控制器为

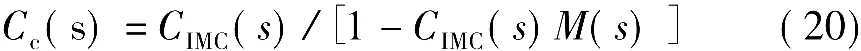
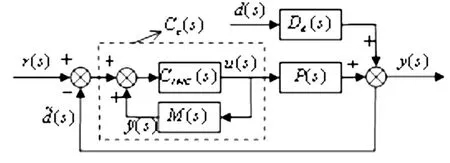
图7 IMC等效结构图

将式(22)和(21)代入式(20)，得到的等效反馈控制器为

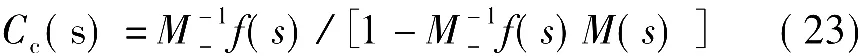
由上式可知，控制器仅有一个可调参数α，其取值直接与系统的响应速度和稳定性能相关。

3.2 实验结果与分析

文献［7］根据鲁棒性能指标提出了一种内模滤波器可调参数的整定方法:

式中，α为滤波器可调参数，β为鲁棒性能指标。该方法明确了可调参数α与鲁棒性能之间的关系，避免了α调整的盲目性。β的取值范围为1.5～2.5，且取值越大，鲁棒性越强。同时，为避免过分放大噪声，α的选取应满足:

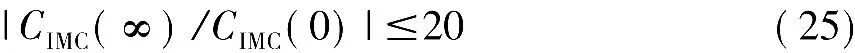
考虑到使用降阶模型产生的模型不匹配，本文取β=1.9，基于用次最优降阶方法获得的降阶模型，获得可调参数α=193.5。同时采用常规PID方法，利用Cohen-Coon整定法PID控制参数为:KC=2.265，TI=403.6416，TD=65.4138。两种控制方法获得液位过程响应曲线如图8所示，并根据实验数据得主要性能参数如表1所示。

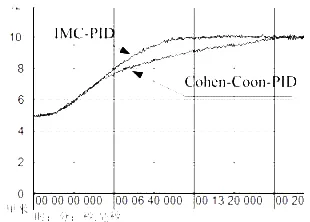
图8 控制响应曲线

表1 系统响应性能参数

分析结果表明，两者超调量相差都很小，采用内模控制器的系统响应的上升时间和调节时间均优于常规PID控制方法。

［1］ 王志新等，双容水箱上的几种液位控制实验及被控对象的数学模型［J］.北京:北京师范大学学报，2006，42(2):126-130

［2］ 王逸隆，江蜀华，Matt James.双水箱水位控制系统的混杂技术［J］.南京:电气电子教学学报，2008，30(3):36-38

［3］ Yu＇e An，Chuanqing Gu.Model reduction for large-scale dynamical systems via equality constrained least squares［J］.Journal of Computational and Applied Mathematics，2010，234(8):2420-2431

［4］ 朱耀麟，杨志海，陈西豪.模型降阶方法研究［J］.北京:微计算机信息，2011，27(5):22-25

［5］ 李国勇.过程控制系统［M］.北京:电子工业出版社，2009

［6］ Xue D，Atherton D P.A suboptimal reduction algorithm for linear systems with a time delay［J］.International Journal of Control，1994，60(2):181-196

［7］ 赵志诚，刘志远，张井岗.一种时滞过程内模PID控制器鲁棒整定方法［J］.沈阳:信息与控制，2010，39(5):526-530