准洛伦兹变换与平面电磁波方程
—— 多普勒效应
杨步恩
(大连理工大学物理与光电学院 辽宁 大连 116024)
1905年,爱因斯坦的《论动体的电动力学》阐明了电磁场的洛伦兹变换,以及相对论多普勒效应[1].
今天回顾历史,将以新的角度来考察该问题,即运用互为共轭的一对变换代替洛伦兹变换,通过“比例中值定理”完成电磁场的洛伦兹变换,给出动系的平面电磁波方程,电磁辐射能流和相对论多普勒效应公式.除此,指明应用极隧射线实验来检验前述论断正确与否的可能性.
1 电场和磁场的共轭变换
根据狭义相对论的基本假设:光速不变性和相对性原理,能够得到一对互为共轭的变换.再通过比例中值定理完成洛伦兹变换.在我们看来,这是任何物理量在变换中出现根号的根本涵义.
如图1所示,设两个参考系,动系K′相对于静系K运动.当原点O′与O重合时,自原点发出光信号,并计时(t=t′=0).在t时刻,光信号波面到达P点.

图1 K′系以速度v运动
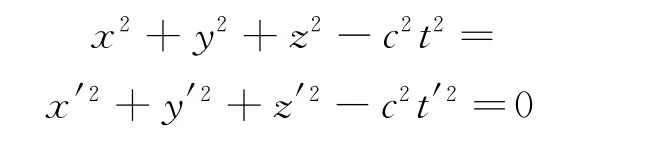
因此,在每个参考系的观察者看来,下述关系必定成立.从此式出发,依据相对论的基本假设,导出一对共轭变换

以式(1)、(2)变换为依据,可以证明电场E和磁场B也有一对互为共轭的变换
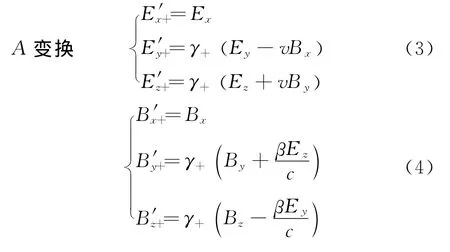

然后,再根据比例中值定理,即
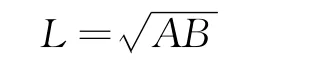
完成洛伦兹变换

2 静系的平面电磁波方程
如果平面电磁波在既无自由电荷,又无传导电流的真空中传播,那么电场E和磁场B只是坐标x和时间t的函数.在此情况下,梯度符号!即蜕化为简单形式

如此,麦氏方程组简化为一维形式
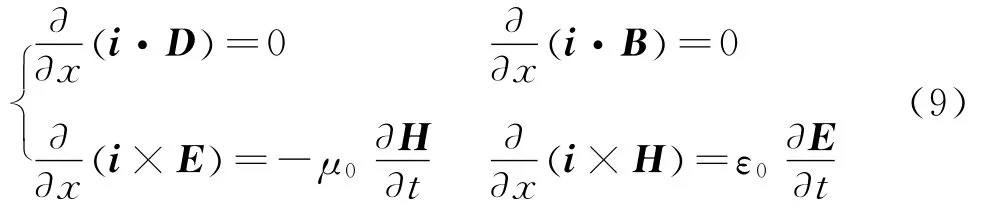
其中D=ε0E,B=μ0H.
由式(9)可以证明随时间t变化的电磁场分量Ex=0,Hx=0,而其余四个分量Ey,Hz以及Ez,Hy均满足波动方程.如
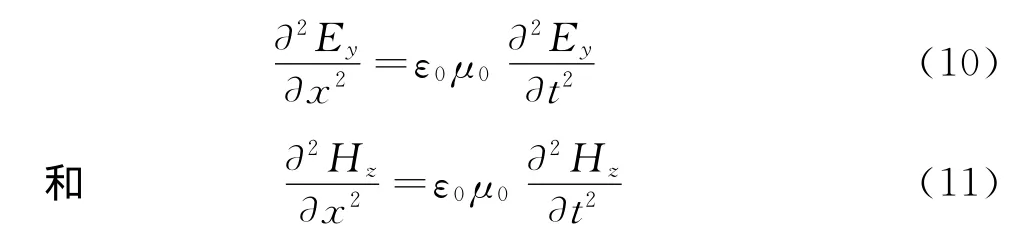
分量Ez和Hy也满足相同形式的方程.
电磁波的波速

如果方程(10)的解是简谐电波

那么,与其伴随的磁波,也必为简谐波
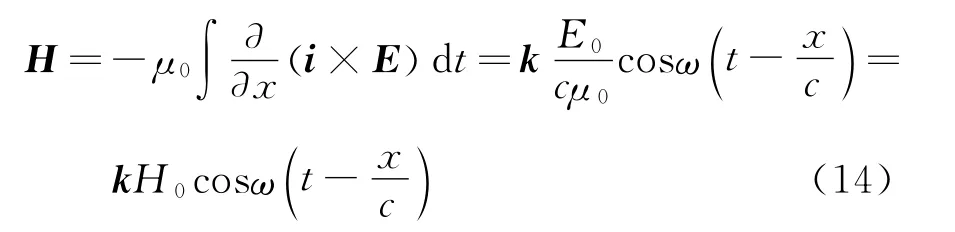
由此可见,平面电磁波的振幅关系是

平面电磁波的能流矢量

3 动系的平面电磁波振幅
根据电磁规律的协变性可知,动系的平面电磁波也有与式(9)相同形式的方程,即

其中D′=ε0E′,B′=μ0H′.
由式(17)得动系的正向平面电磁波方程

下面将对式(18)作共轭变换.由式(3)~ (6),得动系的正向平面电磁波振幅

因此,用比例中值定理完成振幅E′0,H′0的洛伦兹变换为
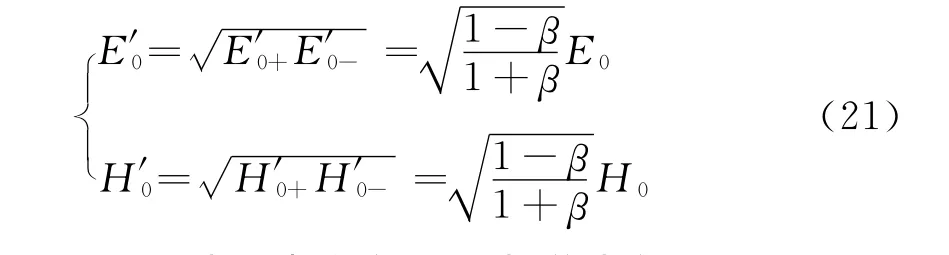
同理,得动系中逆向平面电磁波方程

对式(22)进行共轭变换,得振幅为

因此,在洛伦兹变换下,振幅的变换为
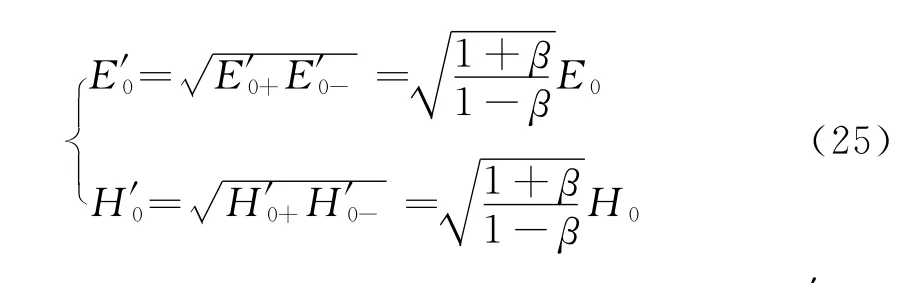
4 电磁波相位的不变性与多普勒效应
下面根据电磁波相位变换的不变性原理,推导相对论多普勒效应公式.
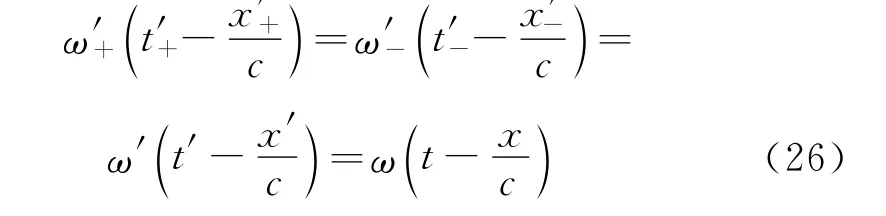
对逆向传播的电磁波而言,相位关系是

分以下三种情况讨论.
(1)相位的A变换
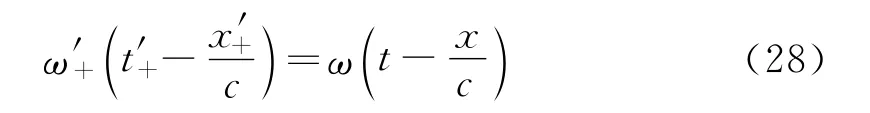
式中的t′+和x′+,按式(1)进行变换,则得

因此,角频率

同理,对逆向传播的电磁波相位,由

(2)相位的B变换
由式(26),知道动系的角频率
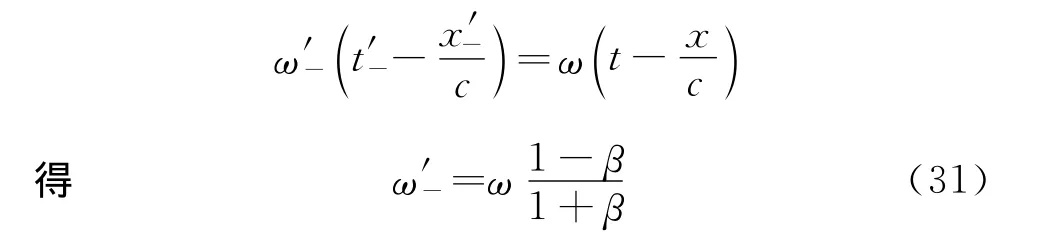
根据式(27),得到动系中逆向电磁波的角频率
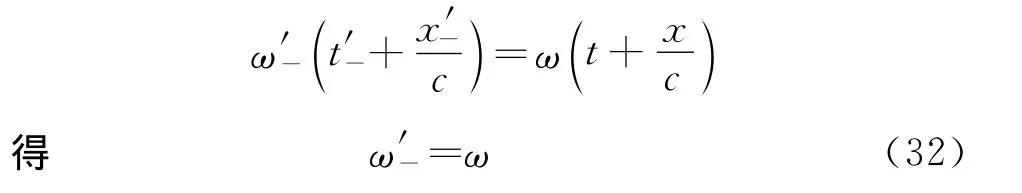
(3)电磁波相位的洛伦兹变换
根据此前给出的角频率共轭变换,运用中值定理来完成洛伦兹变换.
由式(29)和(31),得到正向电磁波频率为

同理,由式(30)和(32)得到逆向电磁波的频率
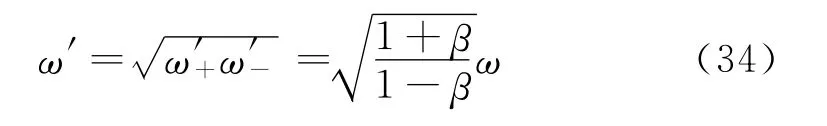
上述频率式(33)和(34),还可以直接对相位

进行洛伦兹变换而得到.
5 动系的平面电磁波方程
根据前述振幅和相位的共轭变换结果,给出动系的正向平面电磁波方程.
A变换,由式(19)得

B变换,由式(20)得
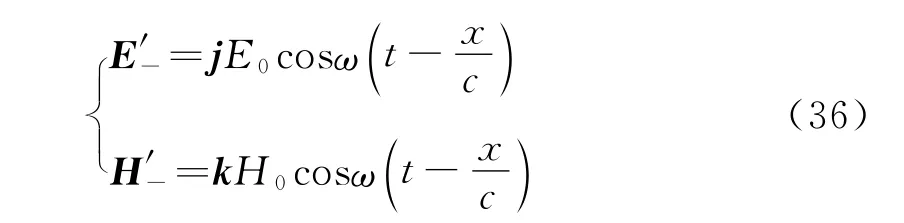
洛伦兹变换,根据比例中值定理得
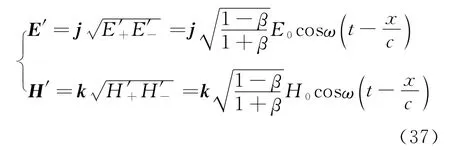
同理,得到逆向传播的电磁波方程
A变换)
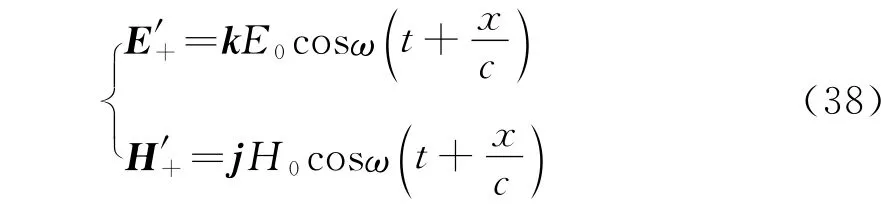
B变换
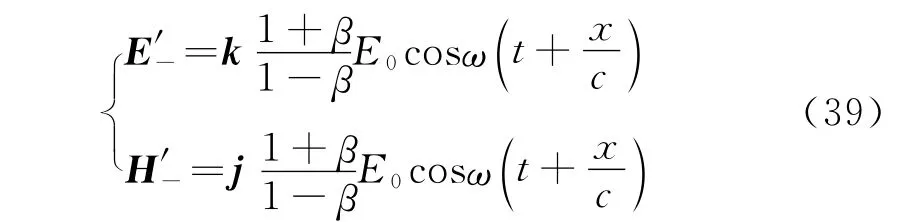
洛伦兹变换
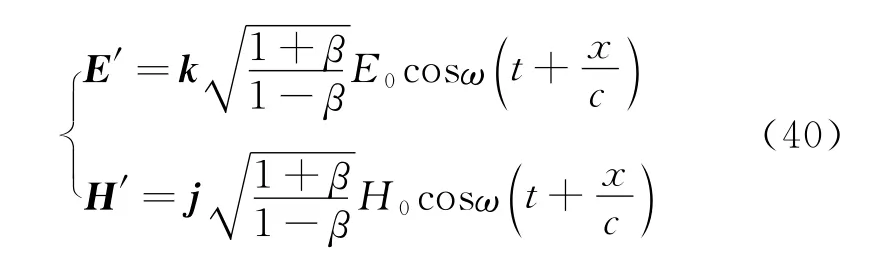
6 动系的平面电磁波能流矢量
根据电磁规律的协变性可知,动系的电磁波能流矢量为

对式(41)进行共轭变换,由式(35)和(36),得A,B变换分别为

然后,由中值定理给出洛伦兹变换下,正向电磁波能流矢量为
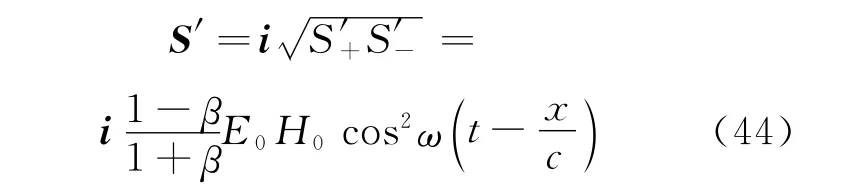
同理,对逆向传播的平面电磁波,也有形式相同的能流矢量
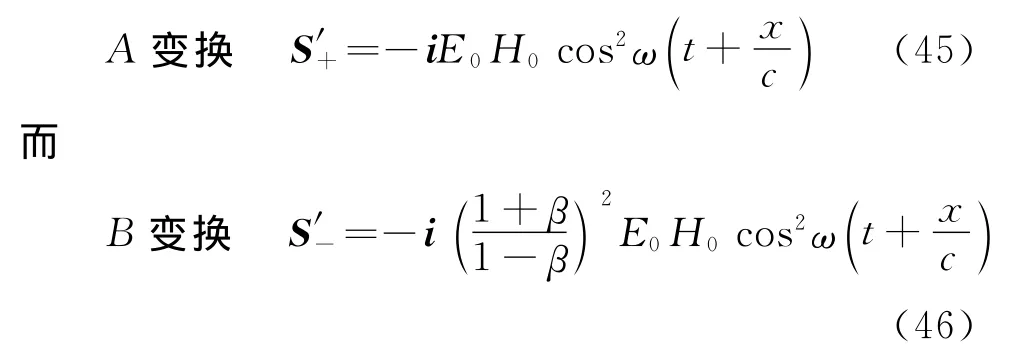
因此,洛伦兹变换下,逆向电磁波能流矢量为
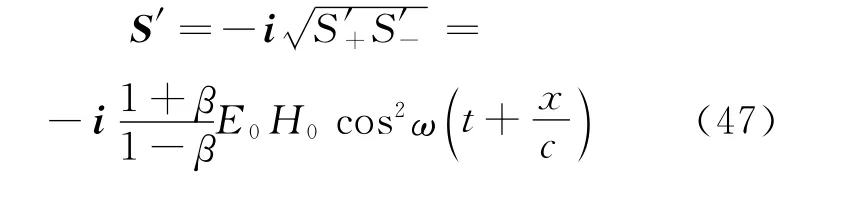
7 结论
(1)静系的平面电磁波方程

(2)动系的平面电磁波方程
A变换

B变换

洛伦兹变换
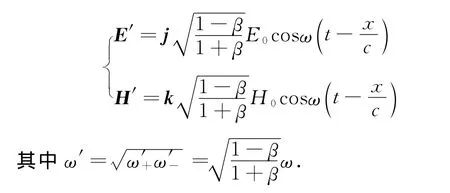
(3)动系中逆向传播的平面电磁波方程
A变换

B变换
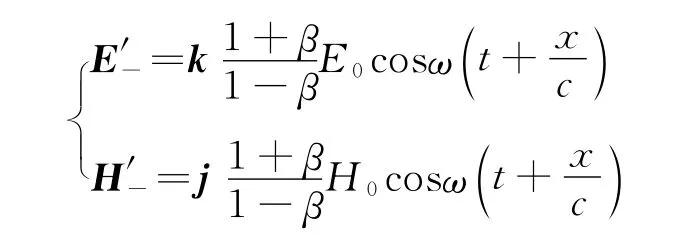
洛伦兹变换

(4)动系的正向平面电磁波能流

(5)动系中逆向平面电磁波能流

8 结束语
根据电磁波相位不变性原理,也可以得到多普勒效应的光频变换
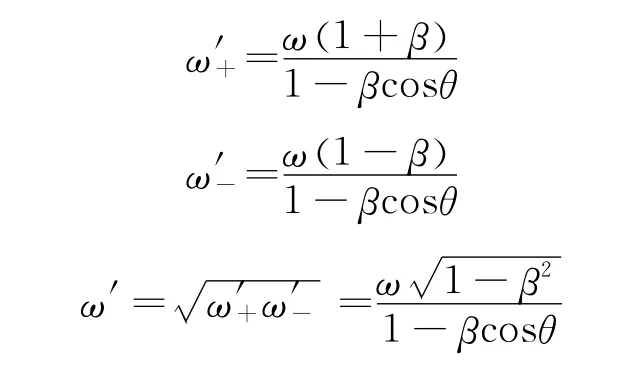
早在相对论创立之初,爱因斯坦阐明测量极隧射线的发射或吸收光频,取决于离子的运动速度,以及光源至接收器连接线的方向(即θ角).因此,借助此现象可用于检验“相位不变性”原理及推论.计算多普勒效应纵向光谱线的位移
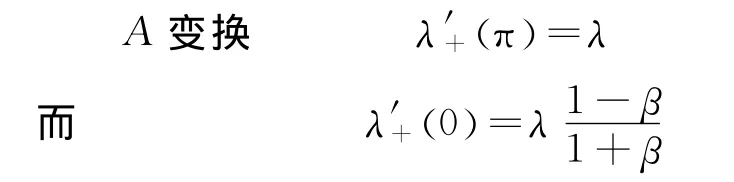
如果以λ为中心,那么纵向谱线移动为
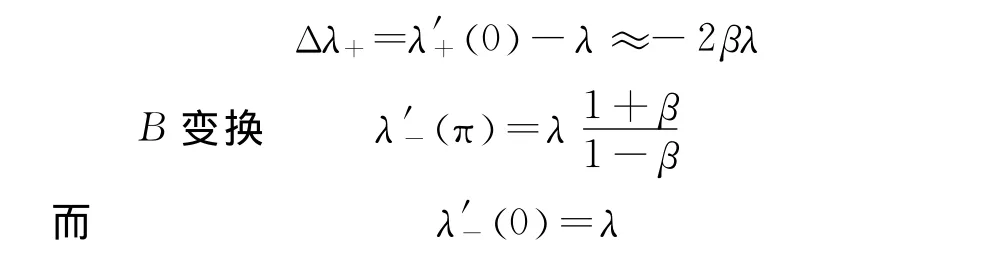
因此,得纵向光谱线移动

洛伦兹变换
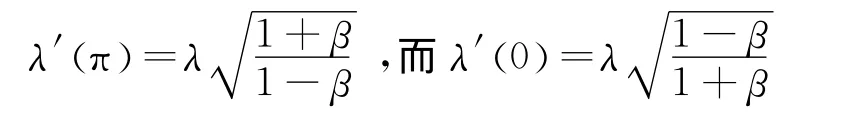
因此,得以λ为中心的纵向谱线移动

上述结论,需要用实验来证实.
1 爱因斯坦著.范岱年,等译.论动体的电动力学(文集第二卷).北京:商务印书馆,1977.83

