柴油中烷烃生成焓和前线轨道能的理论研究

曾秀琳，李敏，居学海

（1.淮南师范学院 化学与化工系，安徽 淮南 232001；2.南京理工大学 化学系，江苏 南京 210094）

为了使柴油在燃烧时表现为抗爆性能好，一般会在柴油中增加易氧化的或是自燃点低的正构烷烃的含量，从而降低不易氧化、自燃点高的异构烷烃以及芳烃在柴油中的含量[1,2]。在石油化工中，评价危险性化合物的爆炸性和安全性的一项重要参数就是生成焓。当然生成焓也是热化学的一项重要的研究内容[3,4]。对于稳定化合物，其实验生成焓可通过查表及各种手册获得；但对危险性化合物，用实验方法来测定这些物质的生成焓是困难的，有时还带有很大的危险性。故借助各种理论方法对物质生成焓加以计算或预估便成为热门课题[5,6]。分子轨道 （MO）方法现已被广泛使用。运用高水平的Ab initio MO 方法（如 QCISD(T)、Gn和 MPn等）基于求精确的总能量而计算生成焓，所耗机时极大，对系列较大分子难以实现。现在，可处理电子相关问题的密度泛函理论 （DFT）,尤其是其中B3LYP方法不仅能计算出可靠的几何构型和能量，而且对计算机的资源要求不高，故成为当前预测和计算化合物结构和生成焓的常用方法。比较计算值与实验值可以得知，B3LYP方法结合6-31+G**基组在计算有机物的生成焓方面具有相对较好的准确度[7]。本文使用B3LYP/6-31+G**方法计算了柴油中烷烃生成焓并准确地预测出含碳原子数较高的直链烷烃的生成焓。同时研究了柴油中烷烃前线轨道能（最低空轨道能ELUMO和最高占有轨道能EHOMO）及其差值（ΔE=ELUMO-EHOMO）。

1 计算方法

以分子CxHy为例，采用原子化反应计算在298 K下的标准生成焓[8]。

首先目标分子CxHy经过原子化反应分解为原子：

此反应在 0 K时的反应热 ΔH0，即目标分子CxHy的原子化能，由下式可以计算得出：

式中：ΔfH0,C，ΔfH0,H以及 ΔfH0,CxHy分别为原子 C、H和分子CxHy在 0 K时的生成焓。因此在0 K时，若已知 C原子和 H原子的实验生成焓ΔfHo(C,0K)，ΔfHo(H,0K)，想要求得 CxHy的生成焓，最关键的一步是求出式 (1)的反应热，由下式可得到式(1)的反应热：

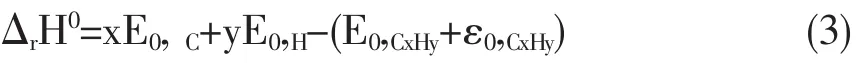
式中：E0,C，E0,H，E0,CxHy和 ε0,CxHy分别是指原子 C，H和分子CxHy在 0 K时的总能量以及分子CxHy在0 K时的零点振动能。由式(3)得到反应热后，由原子 C，H在 0 K时的实验生成焓 ΔfHo(C,0K)以及 ΔfHo(H,0K)，易由式 (2)得CxHy在 0K 时的生成焓ΔfHo(CxHy,0K)。从而进一步得到其在 298 K的标准生成焓ΔfHo(CxHy,298K)即可由下式求得：

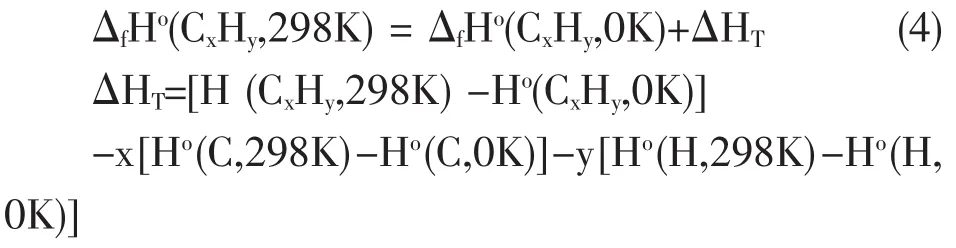
式中：Ho(CxHy,298K)，Ho(C,298K)，Ho(H,298K) 分别是指目标分子CxHy和原子C，H在298 K时的标准生成焓，Ho(CxHy,0K)，Ho(C,0K)和 Ho(H,0K)则分别是指CxHy和原子C，H在0K时的标准生成焓，这些标准生成焓数据都是可以从各种水平计算的热力学数据获得，因此标题物在298 K的标准生成焓ΔfHo(CxHy,298K)即可求得。所有分子及原子都是用B3LYP/6-31+G**方法进行几何构型全优化。在相同计算水平下的频率计算证实所得优化构型为稳定构象，即所有振动频率值为正，没有虚频存在，对应于势能面上的能量极小点。零点振动能的校正因子采用的是0.96[9]。本章节的计算都是采用的Gaussian03程序包完成[10]。

2 结果与讨论

2.1 高级烷烃生成焓的预测

表1 B3LYP/6-31+G**方法计算所得的生成焓与实验值的比较(298 K,kJ/mol)

图1 B3LYP/6-31+G**方法计算所得的生成焓与实验值的比较

表1中列出了 B3LYP/6-311++G**方法计算所得的生成焓值与实验值，经过对比发现两者之间的偏差会随着碳原子数的增加而变大，因此这里是以含碳原子数较少的正构烷烃及其自由基的实验值作为标准（如图1所示），然后对所得到的计算值进行线性回归分析，把所得到的计算值与链烃中的碳原子数相联系，建立了一个一元线性方程，其中以分子中的碳原子数作为自变量，预测生成焓值作为因变量，以便进一步增加计算结果相对的准确性。由含碳原子数为2到6个的正构烷烃的分子计算所得的生成焓的值，通过线性回归分析可得线性方程：

计算所得的 C2～C6正构烷烃的生成焓的平均绝对误差都在误差范围内，通过比较计算所得到的C2～C6正构烷烃的生成焓与实验数据，可以看出两者非常接近，说明B3LYP/6-311++G**方法可以较为准确地预测出含碳原子数较高的直链烷烃的生成焓。

表2中列出的是通过上述一元线性回归方程计算所得的各个正构烷烃的生成焓的结果，通过比较可以看出计算所得的生成焓的值都在误差范围以内。由表2中的数据可以看出，通过计算得到的正构烷烃生成焓的值多数要比实验值大，由此可以看出密度泛函方法还是没有能够达到量子化学理论里面所谓的Kohn-Sham方程极限。另外，由计算所得到的结果分析以及一些文献数据的对比也可以得出，在采用密度泛函方法计算热力学数据时，在选用方法以及基组方面对计算的准确性是非常重要的。

表2 通过线性方程预测的高级烷烃的生成焓与实验值的比较(298K,kJ/mol)

2.2 HOMO-LUMO的能隙

我们知道，物质的EHOMO越高，那么能隙ΔE越小，则电子较易从最高占有轨道向最低空轨道跃迁，从而易于引发热分解和爆炸。通常将此判据称为“最易跃迁原理”（PET）[12]。 即 ΔE 越小，电子最易跃迁，则其最不稳定而发生热分解。本论文对柴油中主要的正构烷烃以及多种主要带有支链的烷烃的初始构型用B3LYP/6-31+G**方法进行了结构优化，并且经过频率分析确定没有虚频，由此就得到了它们的稳定构型。通过对比最高占据轨道(HOMO)以及最低空轨道 (LUMO)能量之间的差别，由此得到各个能隙差 ΔEgap。

由表3可知，对含总碳原子数为 13，15的烷烃而言，ΔEgap大体趋势是随着侧链碳原子数的增加而减小。而且对于含总碳原子数不同的两大类烷烃，计算时特别选用了相对应的结构来研究，它们的ΔEgap的大体趋势也是相近的，图 2中 A表示的是含总碳原子数为 13的烷烃的 ΔEgap的值，B表示的是含总碳原子数为 15的烷烃的 ΔEgap的值，在图中也可看出总的相对应得烷烃中含总碳原子数为13的烷烃的 ΔEgap的值也总是比含总碳原子数为13的烷烃的ΔEgap的值要大。

表3 B3LYP/6-31+G**水平下所得总碳原子数为13和15的同分异构体HOMO和LUMO能量(a.u.)

图2 B3LYP/6-31+G**水平下得到的总碳原子数为13和15的同分异构体ΔEgap的比较

2.3 主链碳原子数相同的前线轨道能

主链含碳原子数一定的部分烷烃的计算结果列于表4。比较最低未占有轨道和最高已占有轨道之间的差值，对于直链烷烃，该差值随着碳原子数增加变化很小，表现在整体趋势上是只有略微的减小；对于含有侧链的烷烃而言，主链的碳原子数相同的烷烃，随着侧链碳原子数的增加，ΔEgap会有少量的减少，即对于主链碳原子数一定的烷烃而言，侧链碳原子数越多它的 ΔEgap会越小。表5中对C9～C16的正构烷烃的 EHOMO，ELUMO以及 ΔEgap进行了比较，图3中可以直观地看出，能隙之间的差值的整体走势是随着碳原子数的增大而随之略微有所减小，而且线性关系较为明显。

表4 B3LYP/6-31+G**水平下所得主链碳原子数相同的与HOMO和LUMO能量(a.u.)

表5 B3LYP/6-31+G**水平下计算所得HOMO和LUMO能量的比较(298K,a.u.)

图3 B3LYP/6-31+G**水平下计算所得HOMO和LUMO能量差值ΔEgap(a.u.)的比较

2.4 结论

通过B3LYP/6-31+G**方法先对含碳原子数较少的烷烃进行计算，并线性模拟出线性方程ΔfHmolecular=-21.08×n-31.32对高级烷烃的生成焓进行预测，所得结果在误差范围以内。烷烃的ΔEgap大体趋势是随着侧链碳原子数的增加而减小。总碳原子数为13的烷烃的ΔEgap的值总是要比相应的含总碳原子数为 15的烷烃的ΔEgap的值要大。对于主链的碳原子数相同的烷烃而言，比较最低未占有轨道和最高已占有轨道之间的差值ΔEgap，随着侧链的碳原子数的增加而有少量的减少。对于C9～C16的正构烷烃而言，能隙之间的差值的整体走势是随着碳原子数的增大而随之略微有所减小，而且线性关系较为明显。

[1]刘振杰.柴油碳数分布的测定探讨[J].当代化工,2003,32(1):60-62

[2]郭晓萍,王占杰.直喷式柴油机燃烧数值计算研究[J].工程热物理学报,2005,26(6):61-64

[3]Manuel A V.Ribeiro da Silva,Maria Agostinha R.Matos,Lui′sa MPF Amaral,Standard molar enthalpies of formation of 2-chloroquinoline,4-chloroquinoline,6-chloroquinoline and 4,7-dichloroquinoline by rotating-bombcalorimetry[J].J.Chem.Thermodynamics,2006,38(1):49-55

[4]RobertAA.Standardmolarentropies,standardentropies of formation,and standard transformed entropies of formationinthethermodynamicsofenzyme-catalyzed reactions[J].J.Chem.Thermodynamics,2006,38(4):396-404

[5]Curtises L A,Raghavachari K,Redfern P C et al.Assessment of Gaussian-2 and density functional theories for the computation of enthalpies of formation[J].J Chem Phys,1997,106(3):1063-1079

[6]Nicolaides A,Rauk A,Glukhovtsev M N,Radom L.Heats of Formation from G2,G2 (MP2),and G2(MP2,SVP)total energies [J].J.Phys.Chem.1996,100:17460-17464

[7]曾秀琳.硝酸酯热安定性的理论和实验研究[D].南京：南京理工大学，2007:7

[8]Curtiss L A,Raghavachari K,Redfern P C,Pople J A.Assessment of Gaussian-2 and Density Functional Theories for the Computation of Enthalpies of Formation[J].J.Chem.Phys.,1997,106(3):1063-1079

[9]Scott A P,Radom L.Harmonic.Vibrational Frequencies:An Evaluation ofHartree-Fock,Meller-Plesset,Quadratic Configuration Interaction,Density Functional Theory,and Semiempirical Scale Factors[J].J.Phys.Chem.,1996,100(41):16502-16513

[10]Frisch M J,Trucks G W,Schlegel H B,et al.Gaussian 03,Revision C.02[CP].Gaussian Inc.,Pittsburgh P A,2003

[11]Check C E,Gilbert T M.Progressive Systematic Underestimation of Reaction Energies by the B3LYP Model as the Number of C-C Bonds Increases:WhyOrganicChemistsShould Use Multiple DFT Models for Calculations Involving Polycarbon Hydrocarbons[J].J.Org.Chem.,2005,70(24):9828-9834

[12]肖鹤鸣.高能化合物的结构和性质[M].北京：国防工业出版社，2004