水汽液界面特性的平衡分子动力学模拟

王宝和，王蕴博，李 群，夏良志，王 刚

(1.大连理工大学化工学院，辽宁大连 116024;2.大连理工大学化机学院，辽宁大连 116024)

水是许多化学反应过程廉价的反应溶剂，也是化工生产过程常用的工质。汽液界面行为是研究水相变传热问题的基础。目前，工程上许多有关水蒸发、水蒸气冷凝、加热干燥等相变传热数据仍主要依赖于实验。随着分子模拟技术的发展，采用分子动力学模拟方法，从分子水平揭示水汽液界面特性的研究，引起了国内外许多学者的极大关注［1－3］。本文拟采用SPC模型，对水汽液界面特性进行平衡分子动力学模拟研究，探讨温度、截断半径、模拟分子数对水汽液界面特性的影响规律。

1 模拟方法

1.1 模拟体系的建立

采用直角坐标系，模拟盒子如图1所示，液相位于模拟盒子的中央，汽相分别处于液相的上下两侧，整个模拟体系中有两个汽液界面。模拟盒子在x、y方向的长度为Lx=Ly=L，在z方向的长度为Lz=3L。

图1 模拟盒子的示意图

对于水的分子动力学模拟研究，采用的势能模型有很多，如 SPC、SPC/E、TIP3P、TIP4P、TIP5P等［4－5］。本文采用SPC刚体势能模型，假设只有不同水分子的O原子之间存在短程L－J势能，不同水分子的H原子之间以及H原子和O原子之间存在长程静电势能。水分子的总势能由短程L－J势能和长程静电势能两部分组成，如式(1)所示［2，3］。SPC模型的势能参数如表1所示，其中qH和qO分别为水分子中H原子和O原子所带电荷，rOH为H原子与O原子之间的键长，θ为两个O—H键之间的角度(即键角)，σO为O原子之间L－J势能的尺度参数，εO为O原子之间L－J势能的能量参数，e为基本电荷(1e=1.6×10－19C)，kB为 Boltzmann常数(kB=1.3806 ×10－23J/K)。

表1 SPC模型的参数值

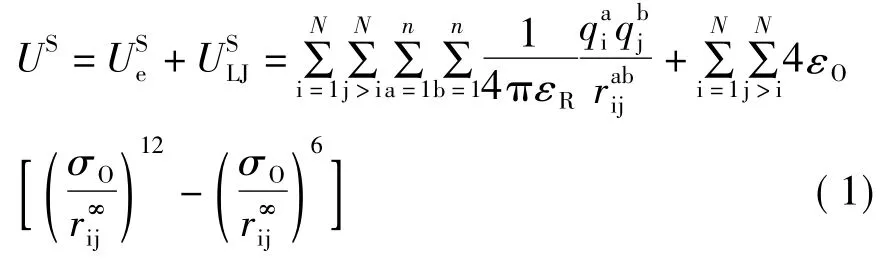
式中:US为总势能，kJ/mol;为长程静电势能，kJ/mol;为短程L－J势能，kJ/mol;N为模拟分子个数;n为每个水分子内受静电作用的作用点数量;i、j为模拟系统内2个不同的水分子;a、b为分子受静电作用的作用点;为i分子中a作用点所带电量，C;为j分子中b作用点所带电量，C;为i分子中a作用点与j分子中b作用点之间的距离，m;εR为真空中介电常数，εR=8.854 ×10－12F/m;i分子和j分子两个O原子之间的距离，m;σO为O原子之间L－J势能的尺度参数，m;εO为O原子之间L－J势能的能量参数，kJ/mol。

对于长程静电势能，采用作用场法。为避免L－J势能和静电势能在边界处发生截断而不连续，导致Hamiltonian函数不守恒问题。采用移位法来处理两种势能，如方程(2)和(3)所示［2－3，6］。

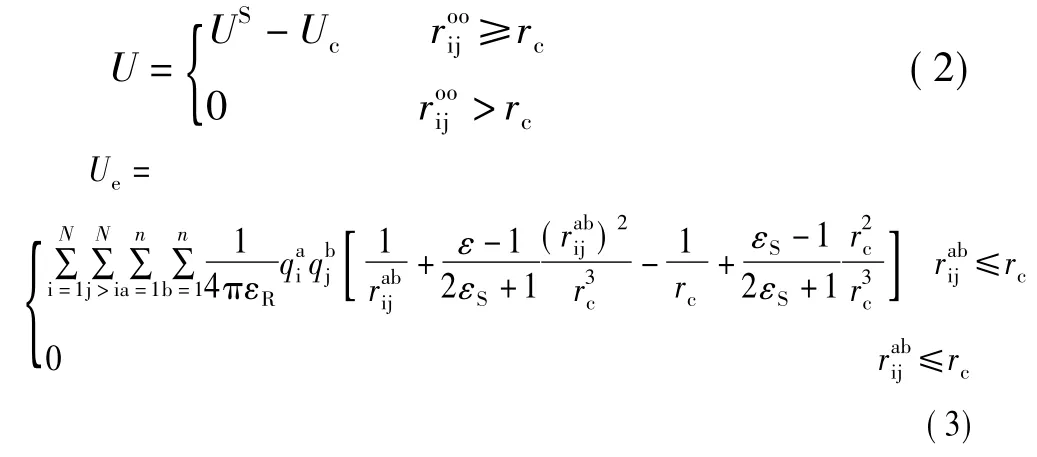
式中:rc为截断半径，m;U为校正后的势能，kJ/mol;Uc为截断半径处的势能，kJ/mol;εS为环境介电常数，通常取 εS= ∞［2，3，6］，因此，式(3)可以简化为方程(4)。

1.2 模拟细节

初始时刻，水分子初始位置为各分子的质心以面心立方晶格(FCC)均匀排列在边长为L的液相模拟盒中，液相区上下两侧的汽相区为真空。水分子质心(即O原子所在位置)为分子坐标的原点，H和O原子均在xy平面上，其中一个H原子位于x轴的正方向上，另一个H原子位于xy平面的第二象限区，O和H的位置矢量分别为rO(0，0，0)，rH(0.3159 σO，0，0)，rH( －0.1053σO，0.2978σO，0)。水分子初始平动速度由随机数发生器随机给定，初始转动速度为0。

在模拟过程中，对物理量进行无量纲化处理;x、y、z三个方向均采用周期性边界条件;保证系统的体积V、温度T和模拟分子数 N保持不变，采用Woodcock变标度恒温法实现系统恒温;不断对体系质心进行矫正，使之处于坐标原点;将模拟盒子沿z方向划分为300个等厚度的薄片;模拟时间步长为0.8fs，总模拟步数为60万步，其中前20万步用于使系统达到平衡，后40万步用于统计界面特性参数。

模拟计算程序是由本课题组采用Fortran语言编写的，其模拟流程如图2所示。模拟运算中所涉及到的方程如式(5) ～ (13)所示［2－3，6］。

图2 模拟流程简图

式中:U(k)为第k个切片的势能，Uij(k)为i、j分子在第k个切片内的势能，nk为第k个切片的分子数，Vs1为切片的体积，ρ(k)为第k个切片的数密度，rij为 i分子和 j分子之间的距离，xij、yij、zij为 rij分别在 x、y、z方向上的分量，、、分别为 i分子中的a原子和j分子中的b原子之间的距离在x、y、z方向上的分量，U()为势函数 U()对的导数，PN(k)、PT(k)分别为第k个切片的法向应力和切向应力，γ(k)为第k个切片的局部界面张力，Δz为切片厚度，γ为汽液界面张力，〈〉为系统统计平均，ρV、ρL分别为汽相主体、液相主体密度，NL、NV分别为液相、汽相切片数，UV、UL分别为汽相主体、液相主体势能(L－J势能、静电势能、总势能)，z(k)为第k个切片的位置，z0为Gibbs汽液界面的位置，d为汽液界面厚度。在统计切片内法向应力和切向应力时，若相互作用的原子a，b均在同一切片内，则计算全部作用;若相互作用原子只有一个原子在某一切片内，则计算一半作用。

2 模拟结果与讨论

2.1 温度对密度分布的影响

在模拟分子数N=256和截断半径rc=0.9498 nm 的条件下，当温度 T=400、450、500、550 和610 K时，模拟得到的密度分布如图3所示。统计得到的汽相主体密度ρV、液相主体密度ρL及汽液界面厚度d如表2所示。由图3及表2可见，汽相主体密度和汽液界面厚度随温度的提高而增加，而液相主体密度随温度的提高而减小。

图3 温度对水密度分布的影响

表2 不同温度下水的汽相主体密度、液相主体密度及界面厚度的模拟结果

液相主体密度与汽相主体密度之差(ρL－ρV)与温度T的关系如图4所示。可见，液、汽相主体密度之差随温度的升高而降低;从理论上讲，在临界点处，其差值应该趋近于零，这与图3所示的规律一致。液、汽相主体密度之差与温度的关系可以拟合成式(14)的形式。

式中水临界温度Tc=647.3 K，利用表2数据对式(14)进行拟合，得到参数 ρ0=1545.8 kg/m3，指数因子x=0.5516。

图4 液、汽相主体密度之差与温度之间的关系

2.2 温度对界面张力的影响

在模拟分子数N=256和截断半径rc=0.9498 nm 的条件下，当温度 T=400、450、500、550 和610 K时，水汽液界面张力的模拟结果见表3。

表3 不同温度下汽液界面张力模拟结果

图5为局部界面张力的分布曲线(500 K)。由图5可见，汽相主体的局部界面张力基本为零;从汽相主体向液相主体的过渡过程中，界面张力值逐渐增加，在汽液界面区达到峰值;在液相主体又在零值附近波动。水汽液界面张力模拟值随温度变化规律如图6所示。

图5 局部界面张力的模拟分布曲线(500 K)

图6 界面张力与温度的关系曲线

由图6可以看出，随着温度的提高，界面张力降低，模拟值与实验值之间的误差逐渐减小。界面张力与温度的关系可以拟合得到方程(15)。

将表3的数据对式(15)进行拟合，得到的参数γ0=254.3 mN·m－1，指数因子 k=1.305。

2.3 温度对势能分布的影响

在模拟分子数N=256和截断半径rc=0.9498 nm 的条件下，当温度 T=400、450、500、550 和610 K时，汽相主体总势能UV、液相主体总势能UL及总势能势阱深度ΔU的模拟结果如表4所示。图7为水分子的势能分布曲线(500 K)，图8为液相主体区域的势能随温度的变化趋势。

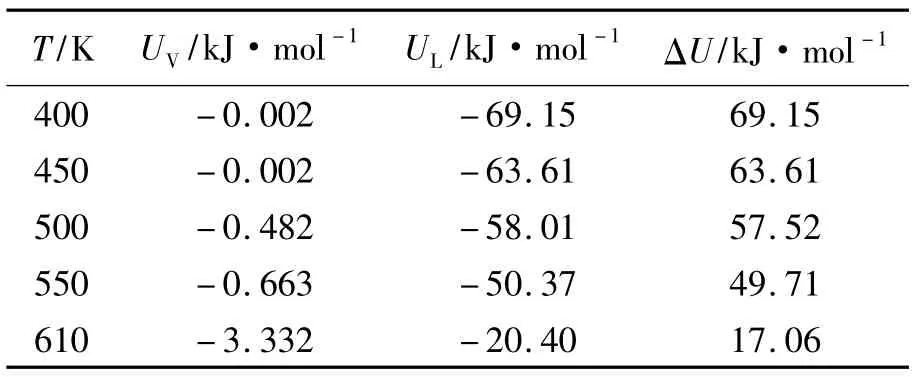
表4 不同温度下水分子势能的模拟结果

图7 水分子的势能分布曲线(500 K)

图8 液相主体区域的势能随温度的变化趋势

前已述及，水的势能分为L－J势能和静电势能。由图7可以看出，L－J势能均为正值，在液相区形成势垒，势垒高度ΔULJ为液相主体L－J势能与汽相主体L－J势能之差;静电势能均为负值，在液相区形成势阱，势阱深度ΔUe为汽相主体静电势能与液相主体静电势能之差;由于静电势能起主导作用，总势能也为负值，同样在液相区形成势阱，分子之间主要为吸引作用。从图8可以看出，汽相主体势能作用不明显，势垒高度随温度升高而降低，液相主体势能的势阱深度随体系温度的升高而减小。

2.4 模拟分子数对模拟结果的影响

在温度500 K和截断半径rc=0.9498 nm的条件下，当模拟分子数 N=108、256、500和864时，模拟得到的密度分布见图9。统计得到的汽相主体密度ρV、液相主体密度ρL及汽液界面厚度d见表5。

图9 水分子数对密度分布的影响

表5 不同水分子数下界面性质的模拟结果

由表5和图9可见，随着模拟分子数的增加，液相主体密度有所增加，液相主体区域宽度加大，汽液界面厚度稍有增大，汽相主体密度有所波动。

2.5 截断半径对模拟结果的影响

在温度为500 K和模拟分子数为864的条件下，当截断半径 rc=0.7915、0.9498、1.2660 nm时，模拟得到的密度分布如图10所示。统计平均得到的汽相主体密度ρV、液相主体密度ρL及汽液界面厚度d如表6所示。从表6和图10可以看出，随着截断半径的增加，液相主体密度增大，汽相主体密度减小，汽液界面厚度变化不大。

表6 不同截断半径下的水汽液界面性质模拟结果

图10 截断半径对密度分布的影响

3 结论

采用SPC模型，对水汽液界面特性的分子动力学模拟研究结果表明，随着温度的升高，汽相主体密度增加，汽液界面厚度增大，液相主体密度降低，界面张力逐渐减小，液相主体区域势能的势阱深度也逐渐降低。随着模拟分子数的增加，液相主体密度增加，汽液界面厚度稍有增大。随着截断半径的增加，液相主体密度增加，汽液界面厚度变化不大。

［1］李印实，何雅玲，孙 杰，等.不同水分子模型凝结系数的分子动力学模拟对比研究［J］.西安交通大学学报，2006，40(11):1272 －1275.

［2］陈正隆，徐为人，汤立达.分子模拟的理论与实践［M］.北京:化学工业出版社，2007.

［3］王蕴博.Mg(OH)2粉体干燥动力学及水分子动力学模拟［D］.大连:大连理工大学，2012.

［4］Jorgensen W L，Chandrasekhar J，Madura J D，et al.Comparison of simple potential functions for simulating liquid water［J］.J Chem Phys，1983，79(2):926 －935.

［5］Mahoney M W，Jorgensen W L.A five－site model for liquid water and the reproduction of the density anomaly by rigid，nonpolarizable potential function［J］.J Chem Phys，2000，112(20):8910 －8922.

［6］Rapaport D C.The art of molecular dynamics simulation［M］.Cambridge:Cambridge University Press，1995.