基于分数阶PI速度控制器的永磁同步电动机控制

王瑞萍 皮佑国

（1.广州民航职业技术学院 广州 510403 2.华南理工大学自动化科学与工程学院 广州 510641）

1 引言

PID控制作为线性最佳控制在工业过程控制中得到了广泛的应用。PID控制器依据对象模型进行设计，方法规范成熟，简单实用，是该控制律得以广泛应用的根本原因。然而，控制对象的现有模型往往是忽略许多时变、非线性等因素而简化得到的。对于高性能的控制系统，上述简化忽略的因素将直接影响系统的性能。为了实现系统的高性能控制，人们一般从建立更加贴近实际对象的模型和改变控制器的适应性两个方向进行研究[1-7]。

有学者将分数阶微积分学引入控制系统，认为“实际系统通常大都是分数阶的”[2]，但是对于分数阶建模，除有分数阶电容器的模型外[3]，尚未取得重大突破。在控制方面，越来越多的研究者关注分数阶微积分理论[4,5]和它在自动控制领域的应用[6-8]，想通过采用分数阶控制器来达到提高系统控制性能的目的[7,8]。近年来，有学者利用分数阶的相关特性，采用分数阶控制器控制整数阶对象，取得了一系列的研究成果。1993年，Oustaloup提出了 CRONE控制器[9]，1994年 Dorcak提出了 PDμ控制器[10]，1999年I.Podlubny将传统的整数阶PD控制器推广到了分数阶情形，提出了分数阶PIλDμ控制器[11]。其中积分与微分的阶次是实数，并得出 PIλDμ控制器性能优于传统PID控制器、且对参数变化的敏感性较小的结论。之后许多学者在分数阶 PIλDμ控制器的参数整定方面作了相关研究，如：Monje等提出了一种PIλDμ控制器的参数整定方法[12]，使系统具有“隔离阻尼”（iso-damping）特性，且有较好的干扰抑制作用，并将所提方法应用于液位系统；Zhao CN等针对一类分数阶系统给出了一种根据增益裕量和相位裕量进行分数阶 PIλDμ参数设计的方法[13]等。

本文以三相交流永磁同步电动机作为控制对象，研究分数阶比例积分（FO-PI）速度控制策略。将电流环校正后的对象作为等效对象，专注分数阶比例积分（FO-PI）速度控制，研究该系统的速度跟随性能。为了公平地评价分数阶控制器的控制性能，与按照最佳设计的整数阶比例积分（IO-PI）控制器的速度系统的跟随性能进行比较。

本文的主要贡献在于：①首次将分数阶速度控制器应用到三相交流永磁同步电动机控制系统中；②在Matlab/Simulink环境下进行仿真，研究FO-PI控制器在阶跃速度给定下的速度跟随性能以及达到的相关性能指标，并与按照最佳设计的 IO-PI控制器的速度跟随性能进行比较；③用自制驱动进行实验，得到FO-PI控制器在阶跃速度给定下的速度跟随性能以及达到的相关性能指标，并与按照最佳设计的IO-PI控制器跟随性能进行比较。

2 控制对象、控制器和设计准则

2.1 控制对象

本文采用的交流永磁同步电动机的参数如下：相电枢电阻为 R=0.29Ω，转矩常数 K=1.83N·m/A(rms)，电气性时间常数 t=19ms，转动惯量J=0.003 41kg·m2。采用矢量控制策略，令id=0后，转速-转矩控制为一典型的电流、转速双闭环控制。电流环采用PI调节器，参数整定后，得到电流闭环等效的惯性环节的时间常数为T=0.001 12s。进而得到控制对象的等效模型为

由于式（1）中的系统增益k可以转移到控制器的Kp中去，而不影响整个控制系统的系统增益，所以，不失一般性，将对象（1）中的系统增益规范化为1。

2.2 分数阶控制器与整数阶控制器

为了进行比较，分数阶和整数阶控制器都采用PI控制器。分数阶比例积分控制器具有如下形式

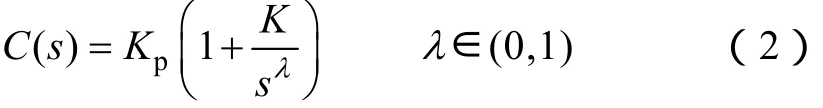
显然，这是通用的包含积分阶次λ 和微分阶次的μ 的分数阶 PIλDμ控制的一种特殊形式（μ=0）。整数阶PI控制器具有如下形式

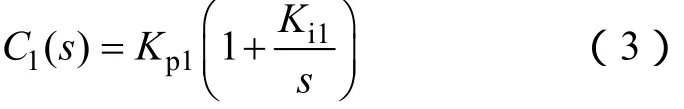
式中，Kp1和Ki1分别为比例和积分增益。

2.3 设计准则

假定截止频率ωc和相位裕度φm已知。为了满足系统稳定性和鲁棒性的要求，由截止频率和相位裕度的基本定理得到如下三个关于开环传递函数Gk(s)的相位和幅值的准则[14]：

（1）相位裕度准则

（2）系统增益变化的鲁棒性准则

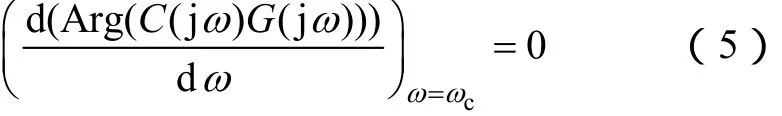
在给定截止频率处，相位的导数为零。也就是说，相位 Bode图在对应截止频率处是平的。即系统对开环增益变化的鲁棒性好以及对于阶跃响应的超调量应几乎不变。

（3）幅值准则

3 FO-PI和IO-PI控制器的设计

由式（1）知，控制对象的幅值和相位的频率为

3.1 分数阶控制器的设计

FO-PI控制器可写为

其幅值和相位的频率表示为

由式（7）和式（10），根据相位裕度准则，Gk(s)的相位可以表示为

由式（13）可得Ki和λ 之间的关系为

由式（15）可建立关于Ki和λ 之间的另一关系式为

显然，由式（14）、式（16）和式（18）三个方程，可以得到三个参数Ki、λ 和Kp的解。

3.2 设计步骤

根据式（14）和式（16），采用作图的方法来求解Ki和λ 。具体步骤如下

（1）给定系统截止频率ωc=200rad/s。

（2）给定期望的相位裕度φm=45°。

（3）根据式（14）、式（16）画出 Ki关于λ 的曲线，如图1所示。

（4）通过曲线交点得到Ki和λ 的图解值。

（5）根据式（18）计算Kp。

图1 Ki与λ 的关系曲线Fig.1 Ki versus λ

通过图1可以得到，λ=0.69，Ki=41.926 2。代入式（18）计算得 Kp=114.797 4。由设计出的分数阶FO-PI控制器画出系统Bode图如图2所示。可以看到，系统的截止频率和相位裕度都满足设计要求；在截止频率处，Bode图中相位曲线是平的；并且满足提出的三个准则的要求。

3.3 IO-PI控制器的设计方法

针对式（1）中描述的运动控制系统，设计如式（3）中描述的IO-PI控制器，可得其频率响应为

图2 采用FO-PI控制器的Bode图Fig.2 Bode diagram with FO-PI controller

通过相位裕度准则，G1k(j)ω的相位表示为

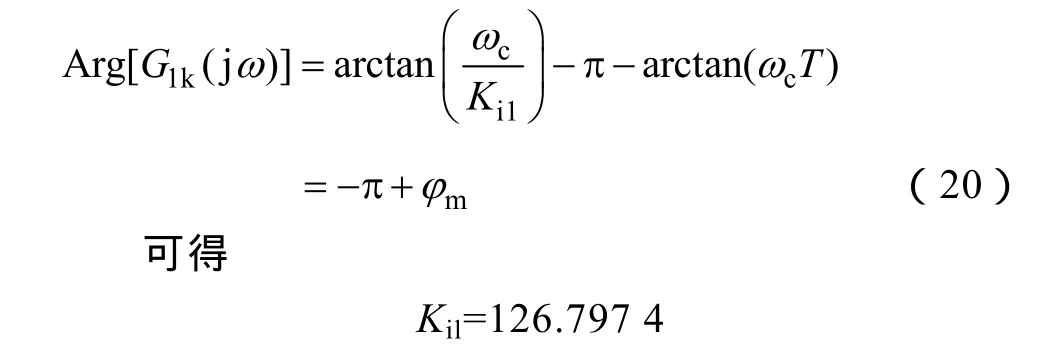
由鲁棒性准则得到

将Kil代入可知，等式不成立。这就意味着设计的 IO-PI控制器不能同时满足相位裕度准则和鲁棒性准则。

为了和传统的整数阶控制器进行比较，根据2.1节给出的电动机的参数且在满足速度超调量σ≤5%的条件下，本文采用工程设计的方法来设计双闭环系统的速度控制器的参数[15]，得到Kpl=2.3，Kil=33。

4 仿真研究

对于分数阶 PIλ分数阶算子 sλ采用 Oustaloup 递推滤波器近似[16]。假设需要逼近的频段为 （ωb, ωh），将 sλ视为一个连续的滤波器，则，用 Oustaloup算法近似的传递函数为

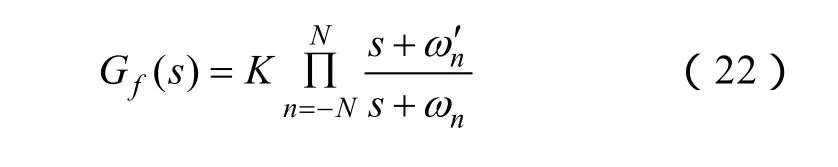
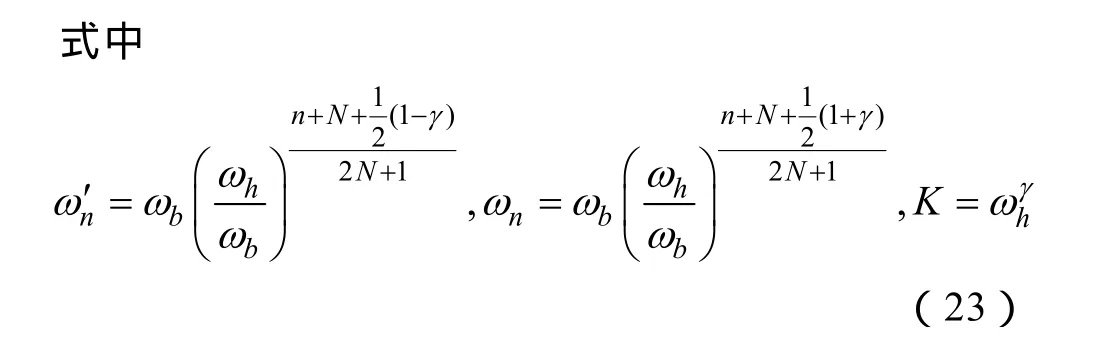
在仿真实验中，为实现分数阶算子sλ的近似，将频率范围选择为从0.000 1Hz到10 000Hz。在T,ωc, τ 和φm一定的情况下，分数阶 PIλ控制器的参数由3.2节得到。

PMSM 控制系统结构如图 3所示，主要包括PMSM、空间电压脉宽调制（SVPWM）、电流调节器（ACR）和速度调节器（IOC/FOC）等。

图3 PMSM控制系统结构图Fig.3 Block diagram of PMSM servo control system

在Matlab/Simulink环境下，按照实际的永磁同步电机模型建模与仿真，采用相同的电流内环，用阶跃信号作为输入，其放大的曲线如图4所示。

图4 阶跃响应曲线Fig.4 Step responses

为了更加直观地比较整数阶控制器和分数阶控制器的跟随性能，表1列出了其主要性能指标：上升时间 tr、超调量δ 和调节时间 ts（±2%稳态值）。可见，采用分数阶控制器的系统动态跟随性能优于采用整数阶PI控制器的系统。

表1 跟随性能指标Tab.1 Tracking performance index

图5为用正弦波和三角波作为输入信号的系统速度输出响应和跟随误差。由图5可见，用正弦波和三角波作为输入信号时，采用分数阶控制器的系统跟随性能优于采用整数阶PI控制器的系统。

图5 采用FO-PI和IO-PI控制器的跟随响应和误差曲线Fig.5 Tracking responses and error signals with FO-PI and IO-PI controllers

5 原型实验研究

实验方案如图6所示，控制对象为日本三洋公司的永磁同步电动机。伺服驱动装置为实验室自制，其中同步电动机采用SVPWM控制策略，控制器采用DSP2812芯片。实验用Ti Code Composer Studio（CCS）软件在PC上执行。

图6 实验装置Fig.6 Experiment plant of PMSM servo drive

根据3.2节得到的Kp是包含控制器和控制对象两部分的比例增益，实验中经过计算取 Kp=0.23。参考文献[17]得到分数阶 PIλ控制器的一种数字实现算法。将分数阶PI控制器算法及其参数和整数阶PI控制器算法及其参数在驱动装置的DSP中编程，实现速度控制器。电流环采用PI控制，其参数经过一定调试后在整个实验过程中保持不变。

实验中电动机转速采用标幺值（pu值），即将速度的实际值除以其同单位的基值。本实验中pu=1，表示转速为2000r/min。

试验中，首先研究在阶跃信号作用下的系统跟随性能，响应曲线图如图7所示，采用±2%作为稳态误差限，可得跟随性能指标见表2。

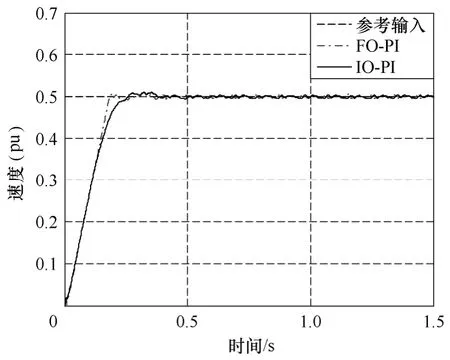
图7 阶跃响应曲线Fig.7 Step responses

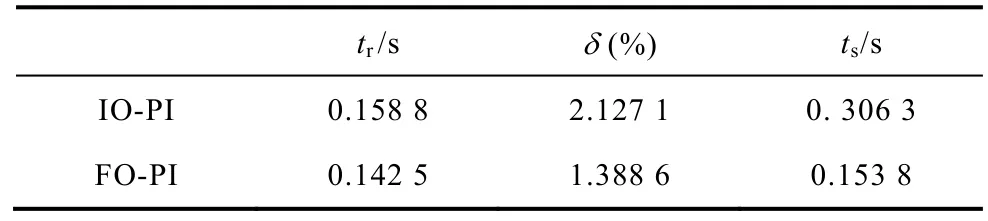
表2 跟随性能指标Tab.2 Tracking performance index

图8a、8b为在实验中采集到的采用整数阶速度调节器的系统三角波速度给定及其输出响应波形和采用分数阶速度调节器的系统三角波速度给定及其输出响应波形。为了能直观地比较整数阶控制器和分数阶控制器的跟随性能，用CCS软件采集数据，然后通过 Matlab软件将采集到的数据显示在同一个图形中，如图9所示。其中9a、9b、9c分别为采用三角波、梯形波和正弦波输入时的速度响应及其对应的误差曲线。

图8 跟随性能实验结果Fig.8 Tracking performance experiment results

图9 采用FO-PI和IO-PI控制器的跟随响应和误差曲线Fig.9 Tracking responses and error signals with FO-PI and IO-PI controllers

从表2和图7～图9可以看出，采用分数阶速度调节器的运动控制系统的速度响应时间要明显快于采用整数阶速度调节器的运动控制系统。在参考输入波形的转折处，采用 IO-PI速度调节器的误差要远远大于采用FO-PI速度调节器的误差。从误差曲线可以看出，采用 IO-PI速度调节器的转速误差都在50r（9%）左右，而采用FO-PI速度调节器的最大误差在 15r（2%）左右。就响应速度和跟随性能来看，仿真和实验结果都表明分数阶速度调节器的系统动态跟随性能要优于采用整数阶速度调节器的系统。

6 结论

本文研究交流永磁同步电动机的分数阶速度控制，在同等实验条件下，分别采用阶跃输入、三角波输入和正弦波输入，对采用FO-PI的速度控制系统与采用 IO-PI的速度控制系统的跟随性能进行了仿真研究和实验室原型实验研究；对于阶跃信号输入的速度响应，以±2%作为稳态误差限测量系统的上升时间、超调量和过渡过程时间等系统性能指标。理论分析和实验研究都表明：FO-PI速度控制器比IO-PI速度控制器具有更快的响应速度和更好的跟随性能，适合于更高跟随性能要求的速度控制系统中作为速度控制器。

[1]Podlubny I.F ractional-order systems and controllers[J].IEEE Transactions on Automatic Control, 1999, 44(1):208-214.

[2]Torvik P J, Bagley R L.On the appearance of the fractional derivative in the behavior of real material[J].J of Applied Mechanics, Transaction of the ASMF,1984, 51(2): 294-298.

[3]Gary W.Bohannan.Analog Realization of a Fractional Control Element –Revisited.2002.

[4]Richard L Magin.Fractional calculus in bioengineering[J].Critical Reviews TM in Biomedical Engineering, 2004, 32: 1-4.

[5]Lokenath Debnath.A brief historical introduction to fractional calculus[J].Int.J.Math.Educ.Sci.Technol.,2004, 35(4): 487-501.

[6]Chen Yangquan.Ubiquitous fractional order controllers[C].Proceedings of the 2nd IFAC Symposium on Fractional Derivatives and Applications(IFAC FDA06, Plenary Paper), 2006: 19-21.

[7]Xue D, Zhao C N, Chen Y Q.Fractional order pid control of a dc-motor with an elastic shaft: a case study[C].Proceedings of American Control Conference, 2006: 3182-3187.

[8]Blas M Vinagre, Chen Yangquan.Lecture notes on fractional calculus applications in automatic control and robotics[C].The 41st IEEE CDC2002 Tutorial Workshop#2, pages1-310.[Online]http://mechatronics.ece.usu.edu/foc/cdc02 tw2 ln.pdf, Las Vegas,Nevada, USA, 2002.

[9]Oustaloup A, Bluteau B.Systems Engineering in the Service of Humans[C].Proeeedings of International Conference on System, Man and Cybernetics, 1993:130-135.

[10]Dorcak L.Numerical models for simulation the fractionalorder control system[EB/OL].Kosice, Slovak Republic:The Academy of Science Institute of Experimental Physics, 1994.

[11]Podlubny I.Fractional-order systems and controllers[J].IEEE Transactions on Automatic Control, 1999, 44(1):208-214.

[12]Monje C A, Vinagre B M, Chen Y Q, et al.Proposals for fractional PIλDμ-tuning[C].Proceedings of the 1st IFAC Symposium on Fractional Differentiation and Its Applications, 2004: 1-6.

[13]Zhao C N, Xue D Y, Chen Y Q.A fractional order PID tuning algorithm for a class of fractional order systems[C].Proceedings of IEEE International Conference on Mechatronics & Automation, 2005:216-221.

[14]Li Hongsheng, Luo Ying, Chen Yangquan.A Fractional Order Proportional and Derivative (FOPD)Motion Controller: Tuning Rule and Experiments[J].IEEE Transactions on Control Systems Technology,2010, 18(2): 516-520.

[15]陈伯时.电力拖动自动控制系统——运动控制系统[M].北京: 机械工业出版社, 2003.

[16]Oustaloup A, Sabatier J, Lanusse P.From fractional robustness to CRONE control[J].Fractional Calculus Appl.Anal., 1999, 2(1): 1-30.

[17]Chen Yangquan.Impulse response invariant discretization of fractional order integrators/dierentiators compute a discrete-time finite dimensional(z)transfer function to approximate srwith r a real number.Category:Filter Design and Analysis, MATLAB Central,http://www.mathworks.com/matlabcentral/ fileexchange/loadFile.do objectId= 21342 objectType= FILE, 2008.