着陆过程中机载相机姿态估计的球面投影方法

侯强 陈茂银 周东华

(清华大学自动化系，北京 100084)(清华大学信息科学与技术国家重点实验室，北京 100084)

基于计算机视觉的自主飞行器着陆技术，是通过飞行器上安装的摄像机或照相机获取着陆区域的景象，利用视频或图像信息获取相机姿态，从而控制飞行器的着陆.20世纪90年代，美国一些大学和研究机构开展了相关的研究［1-2］，设计具有自主能力的无人直升机，实现基于视觉的无人机自主降落.着陆区域采用特殊的几何图形，利用图形随姿态变化规律实时计算相机姿态，实现无人机控制.Tsai等［3］采用“T”字母作为着陆平台的特征标识，张广军等［4］采用双圆图案作为着陆区域的标识物，实现了无人机的视觉着陆导航.这类基于具有特殊几何特征的着陆场坪的姿态估计方法，不仅处理速度较快，而且精度也较高.但这类方法将不适用于一般着陆跑道上的着陆，主要是由于着陆跑道的基本几何特征是两条平行的直线.近年来，国内学者进行了无人机在机场跑道上自主着陆的研究.南京航空航天大学研究小组［5］针对固定翼无人机的着陆问题，采用地平线及着陆跑道的特征，利用射影几何的理论，提出采用地平线获得无人机的滚动角，通过图像中跑道的灭点来解决姿态角求解问题.

本文以机场跑道作为着陆环境，采用机载相机拍摄图像中跑道边缘作为特征，基于球面投影，通过球面的几何性质就可以求出跑道边缘球面投影的交点.相机姿态不同时，跑道边缘的交点在球面上的位置也不相同.本文建立了姿态和球面上跑道边缘交点的对应关系，通过球面上的交点，就可以得到相机姿态.

1 直线的球面投影

球面投影多用于配备有全向(鱼眼)镜头摄像机的系统或应用环境.鱼眼镜头为近似球面，通过全景镜头拍摄的图像会发生较大形变，例如空间中的直线变为圆弧，空间中的平行直线变为相交直线，将图像恢复为人眼视觉可识图像时采用合适的球面投影模型必不可少.采用和图像大小相关的球面模型对平面图像投影，图像中内部元素间的几何关系将被扩大或缩小.

1.1 球面投影模型

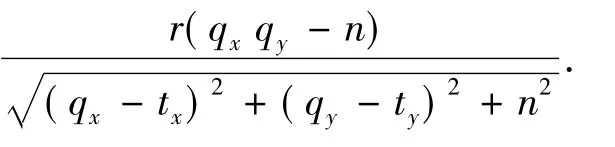
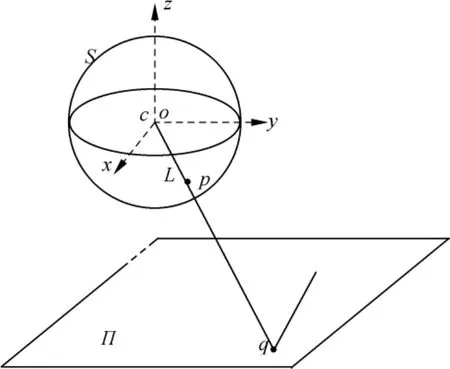
图1 球面投影模型

1.2 直线的球面投影

采用球面投影，空间中的直线经过投影后为球面上的大圆.图像中的直线(线段)经过投影变换后为球面大圆上的一段圆弧.采用检测球面大圆的方法可以实现图像中直线的检测，利用球面圆弧的有限性可以方便实现图像中直线(线段)端点检测［6-11］.

利用球面投影及球面大圆检测图像直线的步骤如下:

①利用Canny算子提取图像的边缘.将提取边缘后的图像二值化处理，边缘点记录为1，图像的其他点为0.

②将二值化图像中的边缘点投影到球面上.投影采用如上的变换关系.

③采用球面霍夫变换［7］的方法检测球面大圆，获取球面大圆参数.

图像中不同直线在球面上的投影为不同大圆.球面的不同大圆必然相交，利用大圆的交点可以求出直线间的交点.

2 姿态估计的球面投影方法

相机固定安装在飞行器上，估计出相机在空间中的姿态就可获得飞行器的姿态.着陆区域的景象在航拍图像中的形态会随飞行器姿态变化而变化.对于机场着陆区，典型的景象特征为机场跑道，一般机场跑道为细长型的矩形区域.航拍图像中由于透视投影，矩形区域发生形变，图像中机场跑道的边缘线将不平行.对图像中机场跑道的边缘延长，将交于一点.采用球面投影，跑道边缘延长线的交点在球面上的投影为边缘线在球面投影大圆的交点.当相机姿态变化时，跑道边缘在球面上的投影将随着相机位置变化在球面上移动，其相应的交点也在球面上移动.通过球面上圆弧及交点的移动可估计相机姿态.

2.1 球面大圆的交点

球面上两大圆的交点可以通过球心和大圆所在平面的法向量求得.球面的大圆和球心确定一个平面.平面间的交线和球面的交点为两球面大圆的交点.通过两相交平面的法向量可求出交线的方向向量，交线经过球心，利用交线就可获得交点.

取球心为原点，大圆所在平面的法向量通过球面大圆上两点获得.两平面法向量的外积为交线的方向向量，且交线通过球心，即通过两平面法向量的外积可获得交线.交线和球面的交点即为两大圆的交点.求解原理如图2所示.

图2 球面交点求解原理

2.2 姿态估计球面投影算法

飞行器在空间中的运动为刚体运动，刚体运动可分解为刚体中心的平移和刚体绕中心的旋转.若固定空间坐标系不动，利用坐标系间的变换，飞行器相对于空间坐标的姿态估计可以转化为飞行器绕其中心姿态变化的估计.

结合相机距离跑道的高度及水平距离，当相机在固定位置拍摄着陆区域时，采用合适的球面投影可以使图像中机场跑道边缘在球面上投影的形状不随姿态的变化而形变，而投影的位置随姿态改变而移动，同理跑道边缘投影延长线的交点亦会随着相机姿态的改变而在球面上移动.由此利用交点在球面上的位置来估计相机的姿态.

图3为相机在空间一点不同姿态下，拍摄机场跑道的图像和图像中跑道边缘在球面上的投影.

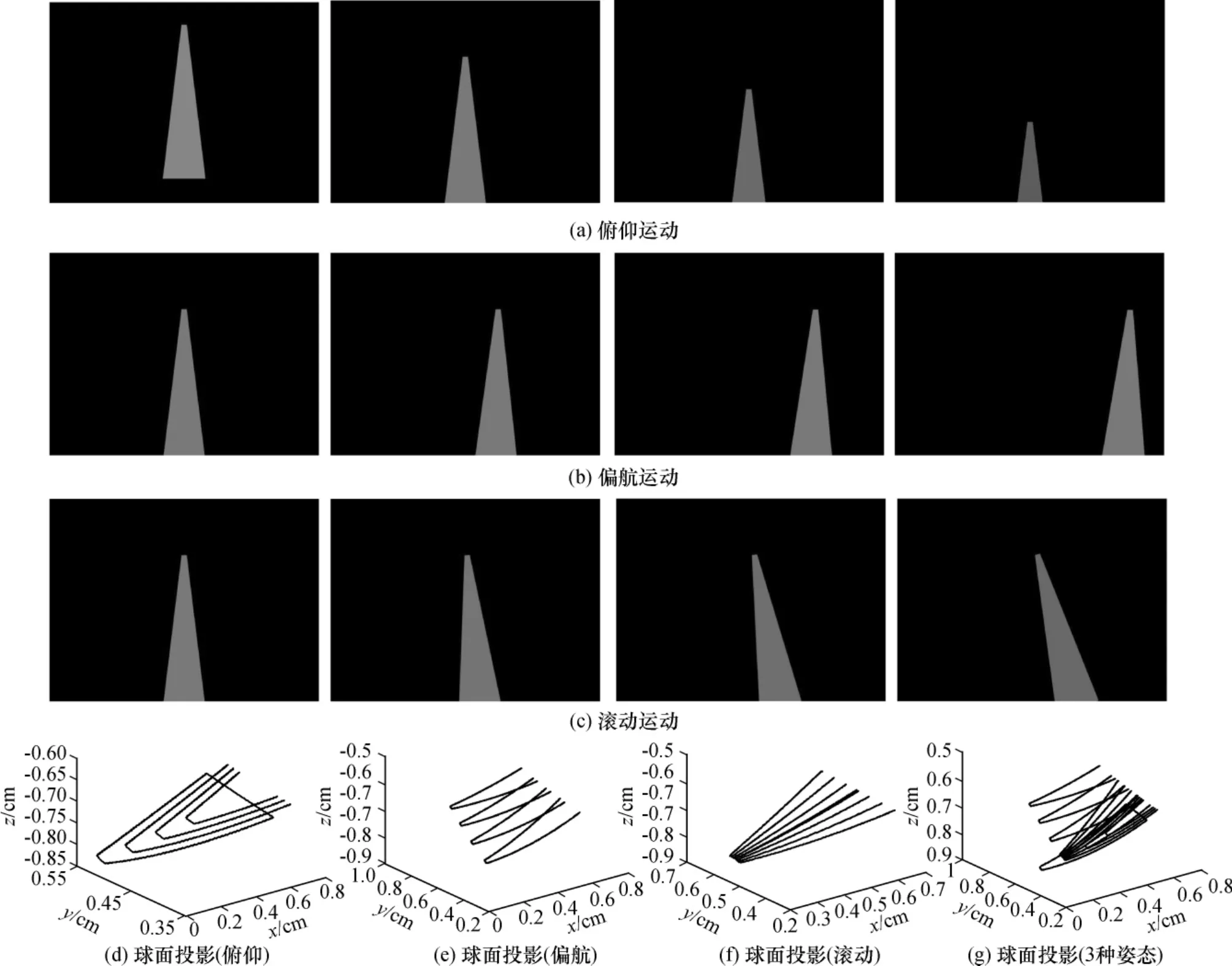
图3 相机姿态不同时跑道边缘在球面上投影

若实现快速飞行器姿态估计，有效的方法是预先计算相机在各个姿态下拍摄的机场跑道在球面上投影的交点，建立为姿态-交点基准数组.飞行器着陆过程中实时拍摄机场跑道，对获取图像进行边缘提取，投影求取交点，搜索姿态-交点数组，确定姿态.

相机距离机场跑道中心的高度和水平距离不同，相机拍摄图像中机场跑道的大小是不同的.如图4所示，相机在不同高度，同一姿态角下拍摄的机场跑道的在图像中占有的区域大小不同.相机到机场中心越远，跑道在图像中的成像区域越小.

图4 相机不同高度拍摄机场跑道的不同成像

在图像球面投影采用的模型中，图像所在平面到原点的距离n为可调参数，n越大投影变得越小.在姿态估计中，相机到机场中心越远，可取n越小，使得跑道在球面上占有的区域大小不变，进行姿态估计时可滤去相机空间位置不同对算法的影响.

算法的详细步骤为:

①离线计算相机在各种姿态下拍摄图像中跑道边缘在球面上投影延长线的交点.设定姿态量化的最小角度，建立姿态-交点坐标对应表.

②相机固定安装在飞行器上，着陆过程中，保持相机相对于飞行器的姿态固定，实时获取图像，对图像提取边缘.

③将图像的边缘投影到球面上，利用上节中提到的方法检测球面大圆参数.

④利用大圆法向量求取大圆间的交点.

⑤在姿态-交点坐标对应表中搜索最近交点坐标，获得相机姿态.

3 实验仿真

图像数据获取来自于虚拟三维仿真环境(见图5)，机场跑道为3200 m×50 m，以机场跑道的中心为空间坐标原点，相机焦距为50 mm，视野为39.598°，远距范围 25.146 m.相机成像的分辨率28.346像素/cm，相机成像大小为640×480像素.将相机放置于200 m高度，距离原点水平距离2000 m位置，不同姿态下拍摄图像.利用拍摄的图像通过文中设计的算法估计相机姿态.

图5 虚拟仿真环境

如表1所示，当姿态角发生变化时，跑道边缘在球面上投影的夹角变化比较小，而跑道边缘在球面上投影的夹角的位置随着姿态角的变化而发生变化.

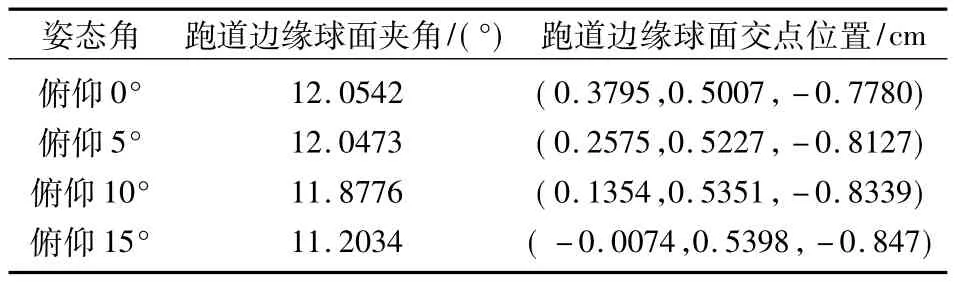
表1 姿态角变化时跑道边缘球面投影的交点及夹角信息

通过实验仿真得到当飞行器存在俯仰和偏航姿态时，利用跑道边缘球面投影交点的位置可以得到飞行器的姿态.当飞行器在不同滚动姿态角下，跑道边缘球面投影交点的位置相同，由此该方法不能很好的分离滚动姿态角.

4 结语

本文主要研究了着陆过程中飞行器的姿态估计.在着陆过程中飞行器拍摄图像中最主要的特征为机场跑道，当飞行器的姿态变化时，图像中机场跑道的位置及形态发生变化，这种变化性主要集中在图像中跑道边缘的交点的位置不同上.利用球面投影可以将机场跑道边缘检测并较方便的得到交点位置，利用交点位置区分不同的姿态，该方法对于飞行器存在俯仰和偏航姿态角时有较好的估计性能，但不能很好的估计滚动角.对于滚动角可以研究采用两跑道边缘球面投影长度的不同来估计.

References)

［1］Saripalli S，Montgomery J F，Sukhatme G S.Visionbased autonomous landing of an unmanned aerial vehicle［C］//Preceeding of IEEE International Conference on Robotics and Automation.Washington，DC，2002:2799-2804.

［2］Sharp C S，Shakeernia O，Sastry S S.A vision system for landing an unmanned aerial vehicle［C］//Preceeding of IEEE Conference on Robotics and Automation.Seoul Korea 2001:1720-1727.

［3］Tsai Allen C，Gibbens Peter W，Stone R Hugh.Terminal phase vision-based target recognition and 3d pose estimation for a tail-sitter，vertical takeoff and landing unmanned air vehicle［C］//Pacific-rim Symposium on Image and Video Technology.Hsinchu，Taiwan，Chi-na，2006，4319:672-681.

［4］张广军，周富强.基于双圆特征的无人机着陆位置姿态视觉测量方法［J］.航空学报，2005(3):344-348.Zhan Guangjun，Zhou Fuqiang.Position and orientation estimation method for landing of unmanned aerial vehicle with two circle based computer vision［J］.Acta Aeronau Tica Et Astronau Tica Sinica，2005(3):344-348.(in Chinese)

［5］刘新华.基于视觉的无人机着陆姿态检测和跑道识别［D］.南京:南京航空航天大学，2004.

［6］Torii A，Imiya A.The randomized Hough transform based method or great-circle detection on sphere ［J］.Pattern Recognition Letters，2007，28(10):1186-1192.

［7］Dell Acqua A，Sarti A，Tubaro S.3D motion from structures of points，lines and planes［J］.Image and Vision Computing，2008，26(4):529-549.

［8］Dorst L，Fontijne D.Geometric algebra for computer science:an object-oriented approach to geometry［M］.Morgan Kaufmann，2007.

［9］Kim H，Lee S.A novel line matching method based on intersection context［C］//Proceedings of IEEE International Conference on Robotics and Automation.Anchorage，AK，USA，2010，2010:1014-1021.

［10］Lopez-Franco C，Arana-Daniel N，Bayro-Corrochano E.Vision-based robot control with omnidirectional cameras and conformal geometric algebra［C］//Proceedings of IEEE International Conference on Robotics and Automation.Anchorage，AK，USA，2010:2543-2548.

［11］Dai B，Pan Y，Liu H，et al.An improved RHT algorithm to detect line segments［C］//Proceedings of IEEE International Conference on Image Analysis and Signal.Xiamen，China，2010:407-410.