基于CSSD-DE通道选择算法的ECoG分类研究

王金甲 尹 涛

1(燕山大学信息科学与工程学院，秦皇岛 066004)

2(河北省计算机虚拟技术与系统集成重点实验室，秦皇岛 066004)

引言

脑机接口(BCI)是一种不依赖于周围神经系统和肌肉，只需利用大脑想象，便可实现与其它设备进行通信的系统。它可以帮助一些由于外周神经或肌肉通道受损而不能正常交流的人们，提高生活质量[1]。BCI系统在大脑上安装多个电极，以准确捕捉事件相关去同步化(ERD)和事件相关同步化(ERS)现象[2]，而电极数量过多，就必然会有噪声和伪迹，通道选择就成为了重要的研究问题。

ECoG称为皮层脑电信号，是直接采集于大脑的皮层处，因此具有信噪比高，信号稳定等特点[3]，对BCI研究具有重要的意义。由脑皮层获得的皮层脑电信号比脑电图信号具有较高的空间分辨率，较宽的频带和较大的振幅，并且比脑磁图信号具有较少的伪迹干扰。近些年来，基于ECoG研究逐渐成为热点。在2004年 Leuthardt等首次使用 EcoG信号在一维空间中对鼠标进行快速而准确的控制[4];Lal等通过提取ECoG信号中的自适应模型系数和通道回归消除方法取得了较好的分类识别效果[5];Graiman等使用小波包分析及遗传算法选择基于事件相关同步和去同步的特征来识别人体的动作[6]。总之提高ECoG的分类正确率是BCI研究的关键问题[7]。

但是ECoG的原理是侵入式的[8]，对受试者的身体造成了很大的创伤。因此通道选择更是ECoG脑机接口研究的重要问题。通道选择研究可以利用特征选择的算法。常用的特征选择算法可以分为两类，一类是基于滤波评价策略的特征选择算法，该算法主要是考虑使用合适的准则评价特征的好坏，跟所选的分类器无关;另一类是基于嵌入式评价策略的特征选择算法，该算法与使用的分类器有很大的关系[9]。基于ECoG脑机接口通道选择近阶段的研究成果主要有：魏庆国等采用遗传算法-共空间模式(GA-CSP)相结合的通道选择算法，应用到ECoG中，最后选出了9个通道达到了92%的识别正确率[10];吕俊等采用二进制粒子群优化算法(BPSO)与CSP相结合的算法，通过参数ρ的取值，得出2个通道就达到92%的正确率[11];赵海滨等将Fisher线性判别分析，L0范数，SVM-RFE三种方法应用在ECoG数据中，得出令人满意的结果[12]。

本研究采用基于微分进化算法的嵌入式特征选择算法，分类器选用逻辑线性分类器。在脑机接口中，对选择好的通道进行特征提取也很关键。共空域子空间分解CSSD作为BCI特征提取的方法已经十分成功[13]。微分进化的目标函数是训练集上选择通道的CSSD特征的分类错误率。因此称这个方法为共空域子空间分解-微分进化算法(CSSD-DE)的脑机接口通道选择方法。当最优通道个数为6，识别正确率达到93%，优于2005年脑机接口竞赛III数据集 I的第1名的正确率91%。此外，提出将最大相关最小冗余度(mRMR)和支持向量机回归特征消去(SVM-RFE)算法应用于通道选择进行对比，实验结果表明 CSSD-DE的正确率最好。

1 基于CSSD-DE的通道选择方法

1.1 微分进化(DE)算法

微分进化算法是求解连续变量全局优化问题的算法，具有简单，快速，鲁棒性好等优点，已经得到了广泛的关注[14]。和其它进化算法不同的是，DE算法的变异算子由种群中任意选取的多对向量的差值得到，而其它的一些进化算法的变异算子是定义的概率分布函数。DE算法主要应用于实参数优化问题，在非线性和不可微的连续空间问题上优于其它进化算法[15]。设 DE算法的种群规模是 P，每个个体有N维变量，则第G代的个体可以表示为Xi，G，i=0，1，…，P-1 。DE 算法的主要算子包括变异，交叉和选择[16]。

当目标向量表示为 xi=(x0，i，…，xN-1，i)T，试验向量为 vi=(v0，i，…，vN-1，i)，i=0，1，…，P-1 时，常用的5种变异算子分别为

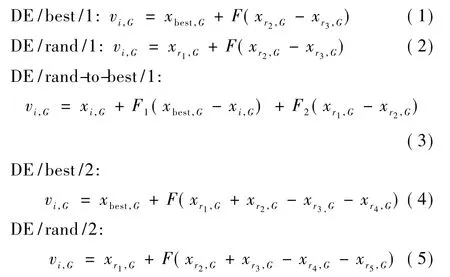
式中，r1，r2，r3，r4，r5∈[0，P-1]，是各不相同的整数，它们与i也不相等，且 F＞0，是一个实数，用于控制差值的放大倍数。

交叉算子是为了增加参数向量的多样性，计算向量 ui=(u0，i，…，uN-1，i)T为

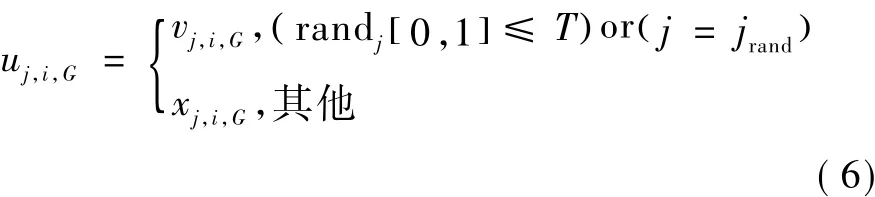
式中，j=0，1，…，N-1，i=0，1，…，P-1，T ∈[0，1]，jrand∈[0，N-1]，T是交叉概率。如果T值较大，DE收敛速度较快，如果T值较小，DE鲁棒性会更好，但同时增加问题的执行时间。

选择算子根据式(7)选择下一代个体，假设所求全局优化问题为求解最小化问题。

如果ui对应的目标函数值比xi对应的目标函数值小，ui将取代xi进入到下一代种群中，也就是说xi，G+1将被设置为ui的值;否则将在下一代种群中保留 xi，也就是说 xi，G+1的值被设置为 xi的值。

微分进化算法主要进行3个参数的调节，分别为差分向量的放大系数F，交叉概率T以及种群大小P。F控制DE的收敛速度，T对DE起到微调的作用，P越大搜索能力越强，但会增加DE计算量。

1.2 共空域子空间分解(CSSD)

将选好的通道数据用于CSSD算法进行特征提取，CSSD的算法可以用源分解的模型来描述[17]。假定XA和XB分别是两种不同任务模式诱发的脑电信号，采样复合源的模型来描述事件相关脑电信号XA和XB

式中，SA和SB分别代表任务A和任务B的源活动，CA和CB分别是由两种源活动相应的空间模式组成，空间模式为源活动在头皮各电极分布的权重向量;SC是两种任务下共有的源活动，CC由SC的空间模式组成。CSSD方法的目标是提取出原始脑电信号中与任务A和B相关的特定成分CASA和CBSB。用CSSD算法设计的空域滤波器表示为对应任务A的FA和对应任务B的FB。设X是原始多导联的脑电信号，可以得到与 X中任务相关的脑电成分为：

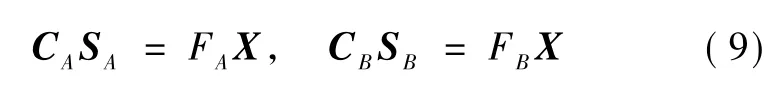
与任务A相关的成分CASA在A任务模式下的能量高于B任务模式，而与任务B相关的成分CBSB在B任务模式下的能量则高于A任务模式。在脑电模式分类问题下，通常把任务转化为提取与任务相关的源活动，即SA和SB[18]。

1.3 基于CSSD-DE的通道选择算法

通过微分进化算法选择通道子集的过程如图1所示。经过带通滤波以后的ECoG数据首先通过微分进化算法进行通道选择，然后选出的通道子集输入到CSSD中进行特征提取，最后提取的特征矢量输入到逻辑线性分类器中进行分类，得出的目标函数值被返回到微分进化算法中作为所选通道子集的评价标准。通过不断迭代，直到最后获得了一个最低目标函数值的通道子集。

图1 基于脑机接口通道选择的流程图Fig.1 The flowchart of channel selection for brain computer interface

当使用微分进化算法进行通道选择时，种群编码方案如下。假设一个群体有20个个体，每个个体用n位二进制字符串表示，n即代表ECoG中的通道个数。微分进化算法对这样的字符串群体进行操作，通过优化目标函数来选择通道数。当任意一位的数值为1时，表示这一位对应的通道被选中，如果数值为0时，表示这一位对应的通道被消去。由于通道选择的目标，一方面是降低想象任务识别的错误率，另一方面是降低识别过程中的成本，即减少通道的个数[10]。因此引入正则化方法，基于正则化参数λ(0＜λ＜1)的目标函数为f(z)=λf1(z)+(1-λ)f2(z)，其中 z为选择的通道，f1(z)代表一个选择的通道子集所产生的错误率;f2(z)表示所选的通道子集个数占总的通道数的比例。在本次实验中设λ=0.7，使用微分进化算法时变异算子采用公式(2)即 DE/rand/1，交叉算子采用式(6)，选择算子采用式(7)。设最大迭代次数为200，差值放大倍数 F=1，种群个体数为20，种群规模64为ECoG的通道个数。在整个过程中，只有训练集参与通道选择，训练集错误率都是通过十倍交叉验证获得。最后将选择的通道子集应用到测试集中得到分类结果。

2 相关特征选择方法对比

2.1 最大相关最小冗余度(mRMR)

mRMR称为最大相关最小冗余度，是一种基于互信息的特征选择算法，由于该算法是单纯地考虑评价特征的标准，与所选择的分类器无关，因此它属于基于滤波的特征选择算法。mRMR是根据交互信息的最大统计独立标准来研究怎样选择好的特征，但是在实施最大统计独立标准时存在一些问题，因此采用另外一种等价的形式，即最大相关最小冗余度的统计标准[20]。

最大相关指的是在每个特征xi和类别C之间互信息的平均值最大，表示为

最小冗余度是指两个特征之间要彼此很独立，如果其中一个特征被移除时，类别的区分能力不会下降很多，表示为

将这两个标准联合起来就是mRMR(最大相关最小冗余度)，定义该函数为maxφ(D，R)，φ =DR，假定已经有特征集Sm-1，这个特征集中有m-1个特征。从剩下的特征集{X-Sm-1}中选择第m个特征，选择特征的过程通过最大化函数 φ来实现。整个搜索过程为[21]

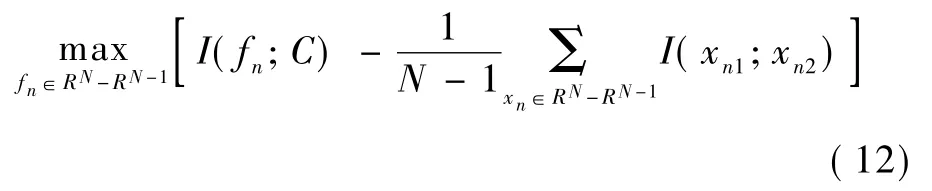
2.2 支持向量机回归特征消去(SVM-RFE)

基于支持向量机的回归特征消去算法是由法国学者I.Guyon提出的，在对特征进行排序时使用支持向量机判别函数的信息来实现[22]，而 RFE(回归特征消去)可以保证在特征排序的过程中保留最优特征子集，将这两者结合起来，就可以得到一个最优特征集合的排序。RFE回归特征消去方法是一个循环的过程，首先用当前数据集训练分类器，根据分类器获得所使用特征的相关信息。其次，根据特征的相关信息，得出所有特征的排序准则值，最后，在当前数据集中移除对应于最小排序准则值的特征。该算法执行到特征集中最后一个变量时停止，最后输出的结果是一系列按特征重要性进行排序的特征编号[23]。SVM-RFE是使用支持向量机中最优分类面的权系数向量作为特征排序标准的，因为在筛选特征时结合分类器进行判别，因此该算法属于嵌入式的特征选择算法。

3 实验结果与分析

3.1 实验数据描述

因为ECoG的信号采集原理是将金属电极放置在大脑皮层来探测信号的，对人的大脑是侵入式的，在实验阶段采集实际的在线数据有一定的困难。2008年脑机接口竞赛数据(BCI Competition IV dataset IV)中的目标是从大脑皮层记录的ECoG信号中预测单个手指的弯曲程度，是一个回归问题，不方便进行分类实验。因此采用ECoG实验数据采用公开的 2005年脑机接口竞赛数据[24](BCI Competition III dataset I)进行仿真。BCI Competition III dataset I有278个训练数据和100个测试数据，每个数据有64个通道，它是由德国的Tuebingen大学提供。在采集数据的过程中，采用8 cm×8 cm的脑皮层64导电极，它完全地覆盖了大脑右侧的运动皮层区，每次实验一共有4 s的想象时间，是从第1 s到第5 s。受试者根据提示来想象左小手指运动和舌头运动，这两种想象任务都是随机出现的，每次实验的持续时间是7 s，采样率为1000 Hz。为了减轻计算负担，对原始数据进行降采样，采样率为100 Hz，然后采用8～30 Hz带通滤波器进行滤波。训练数据包括278次任务实验，包括139次属于类别‘1’，是指想象左手小手指运动;139次属于类别‘-1’，是指想象舌头运动，而测试数据包括100次任务实验，最后目的就是对测试数据判断类别，即判断是类别‘1’还是类别‘-1’。以下实验所采用的分类器均为逻辑线性分类器。

3.2 实验仿真结果记录及分析

3.2.1 CSSD-DE方法实验结果记录

在CSSD-DE通道选择方法中，每次的训练集错误率都是通过十倍交叉验证获得。表1是当取不同的交叉概率(T)进行CSSD-DE算法的不断迭代以后所得出的最优通道个数，将这些最优通道数分别应用到训练集和测试集中进行分类，所得出的实验结果。

由表1看出，当T取值不同时，最后的结果也不同，T取0.7时，最后选择的通道个数为11，分别是[12，15，30，33，35，45，47，50，56，58，63]。将这些通道应用于测试集时，错误率为0.080，f(z)的值为0.1076。而全部通道用于测试集时，错误率为0.110，f(z)的值为0.3770，与后者相比，前者的错误率降低0.030，f(z)的值减少0.2694。由于BCI Competition III dataset I的64个电极通道是按照自上向下，自右向左的顺序逐行编号的，因此对取不同的T所得出的通道进行比较，得出标号为12，21，30，31的通道被选中的几率较大，因此这些通道对运动想象任务下的ECoG的分类识别很重要。说明通过微分进化算法选出的通道子集的分类表现要优于使用所有通道的分类表现。

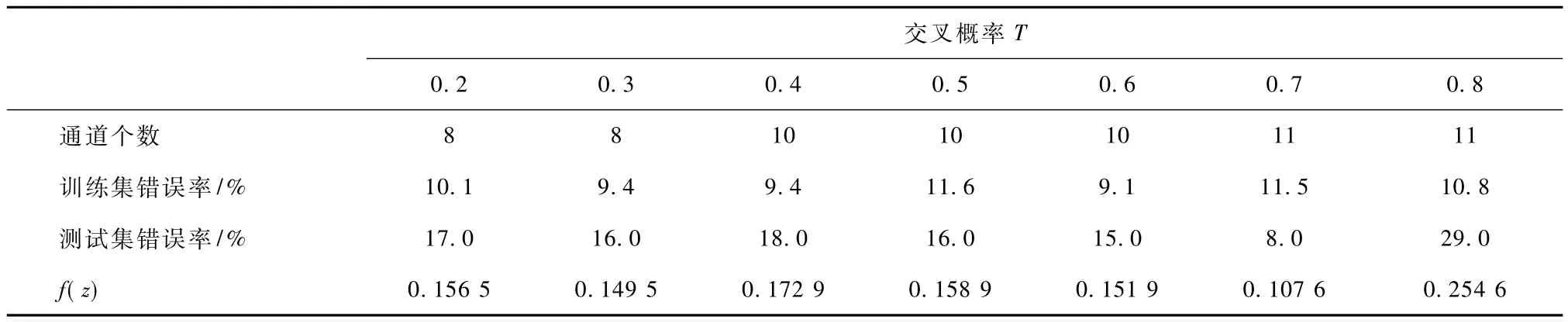
表1 CSSD-DE通道选择方法的输出结果Tab.1 Results of CSSD-DE channel selection method

但是，由于本实验数据所采集的通道个数是64个，微分进化算法要进行264次搜索才能得到全局最优的结果，这是十分耗费时间的。因此本研究采用了一种减少微分进化算法搜索次数的改进方法，即固定选择的通道个数，具体策略见文献[25]。这样就会大大减少搜索的时间，并且也可以找到最优结果。称之为CSSD-DE2算法。

在CSSD-DE2算法中，每次的训练集错误率都是通过十倍交叉验证获得，表2是 CSSD-DE2算法取不同的T进行不断迭代后所得出的最优通道个数，将这些最优通道数分别应用到训练集和测试集中进行分类，所得出的实验结果。由表2可知，当交叉概率T取0.6时，目标函数f(z)的值最小，相应的测试集错误率最低。

表2 CSSD-DE2算法的通道选择方法输出结果Tab.2 Results of CSSD-DE2channel selection method

将CSSD-DE通道选择算法所得的最优结果和运行效率与CSSD-DE2算法的最优结果和运行效率进行比较，并且将所提出的这两种算法与文献[13]中提出的GA-CSP通道选择算法的最优结果和运行效率进行对比，对比结果如表3所示。

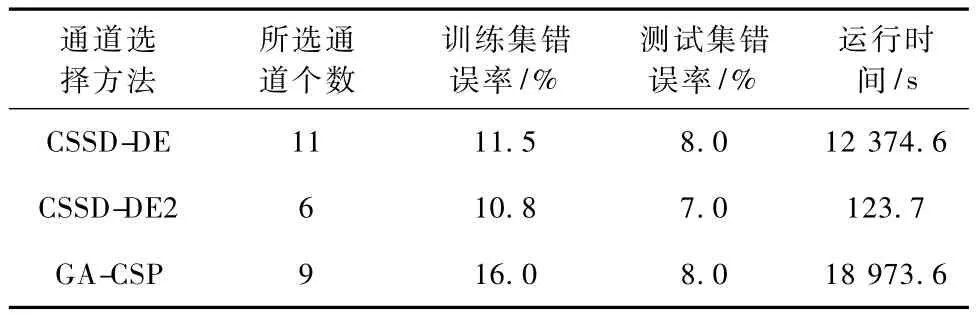
表3 3种通道选择算法输出结果和运行速度对比Tab.3 The contrast of the results and the running speed of three channel selection algorithms

由表2和表3可以看出，CSSD-DE2算法达到了93%识别正确率的效果，而且选择的通道个数从11个降到了 6 个，为[12，26，38，48，57，59]，f(z) 的值从0.1076降到了0.0771，降低了0.0305，搜索时间也大大地缩短了。而将这两种算法与GA-CSP从最优结果和运行效率上进行对比，由表3可知，CSSD-DE2算法选择的通道个数为6，测试集错误率为7.0%，优于GA-CSP算法所选出的9个通道和测试集错误率8.0%。而且从运行速度上看出，CSSDDE和CSSD-DE2算法的运行时间要大大少于GACSP算法，运行速度优于GA-CSP算法。这是由于微分进化算法是目前比较新的进化算法，它无论是从搜索速度还是运行复杂度上都要优于遗传算法。而以往的竞赛结果表明，CSSD的特征提取算法要优于CSP特征提取算法，因为它预先定义了一个伪白化矩阵。实验说明CSSD-DE算法无论在搜索时间还是搜索结果上都有了很大的改善。

3.2.2 mRMR通道选择算法实验结果

使用mRMR对实验数据进行特征排序，每个通道采用300个采样点的方差作为mRMR的输入，K为所要选择的通道数。得出的通道重要性排序[39，2，1，10，3，33，4，57，49，11，41，34，27，56，8，58，35，63，55，48，18，20，42，50，47，43，17，5，19，24，12，6，37，64，32，28，59，25，46，45，51，16，13，36，7，62，26，9，15，40，31，44，54，14，23，21，22，29，52，60，30，38，53，61]。得出的结果如表4所示，其中目标函数f(z)=λf1(z)+(1-λ)f2(z)，λ取不同的值。

表4 mRMR得出的特征的测试集错误率及目标函数值Tab.4 The error rate of the test set and objective function values of mRMR channel selection algorithm

从表4中看出，λ=0.9，K =7，f(z) =0.1279; λ =0.7，K=7，f(z)=0.1238; λ =0.6，K=7，f(z)=0.1218。这三组分别是其对应参数的最小值，选出的通道个数和错误率都得出了比较令人满意的结果，即当通道个数为7时，错误率为0.130。因此mRMR方法比较适用于该竞赛数据，可以在较短时间内选择出较令人满意的通道。

3.2.3 SVM-RFE通道选择算法实验结果

使用SVM-RFE进行特征排序，每个通道取300个采样点的方差作为SVM-RFE的输入，输出结果是通道重要性的排序，得出的通道排序结果为[2，12，18，58，43，30，11，19，21，6，3，37，40，8，1，27，4，24，10，5，57，49，45，53，34，52，14，17，29，62，31，47，54，6139，16，23，7，35，50，60，59，9，64，25，46，55，51，42，44，38，36，56，26，28，33，48，22，41，20，13，15，32，63]。同 mRMR 方法的评价标准一样，通过λ的不同取值，比较目标函数的值。

从表5中可以看出，而当 λ =0.7，K=3或6时，f(z)=0.1611是最小值，当λ=0.6，K=3时，f(z)=0.1447是最小值。这说明当该通道选择算法选出少数的特征时，测试集错误率大于使用全部特征得出的错误率，但是目标函数值大大减小。

3.2.4 CSSD-DE与其相关通道选择算法的结果对比

将所提出的CSSD-DE通道选择算法及CSSDDE2算法，与其它通道选择算法和文献结果进行比较，如表6所示。

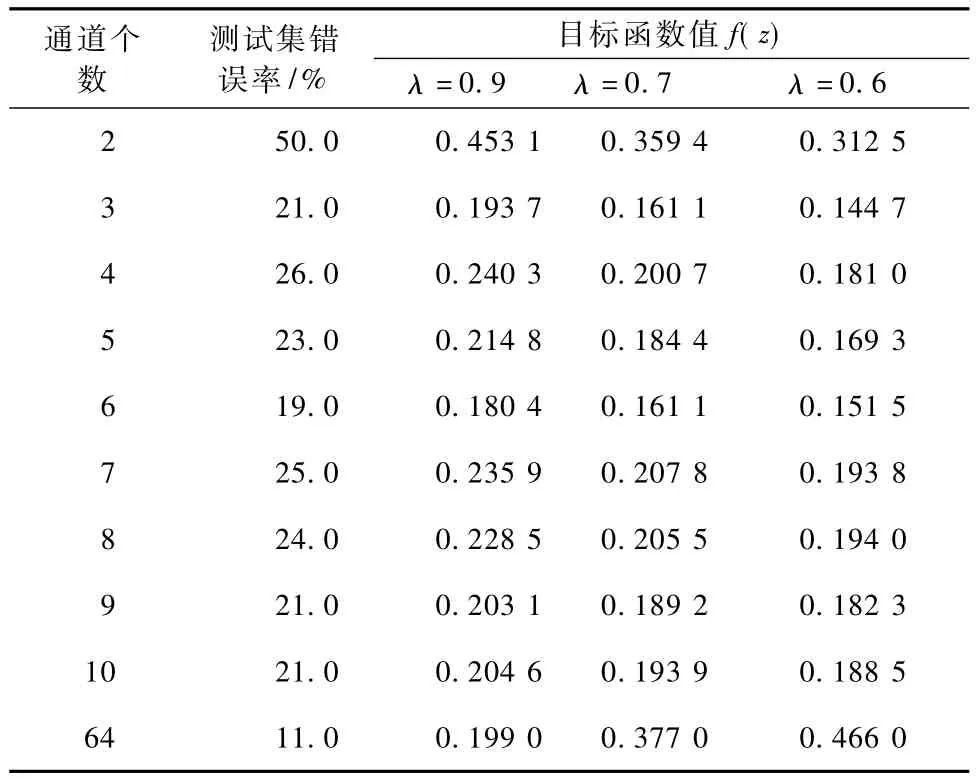
表5 SVM-RFE得出的特征的测试集错误率及目标函数值Tab.5 The error rate of the test set and objective function values of SVM-RFE channel selection algorithm

表6 不同通道选择方法的错误率比较Tab.6 The contrast of the results of different channel selection algorithms

由表6中可知，CSSD-DE2算法的测试集错误率要低于其它通道选择算法，说明CSSD-DE2算法在脑机接口通道选择中有一定的研究价值，对通道选择方面有较大的贡献。

将所提出的CSSD-DE2算法的实验结果与BCI竞赛前三名的实验结果进行比较，如表7所示：

表7 CSSD-DE算法与BCI竞赛结果的对比Tab.7 The contrast of the results of CSSD-DE algorithm and the competition of BCI

由表7可知，使用所提出的CSSD-DE方法对通道进行选择，剔除冗余通道，再进行 CSSD特征提取，显著提高了识别正确率，优于 BCI竞赛三数据一的前3名。

4 结论

笔者研究了ECoG分类中的通道选择算法，提出了 CSSD-DE通道选择算法，并应用到 BCI Competition III dataset I中。

CSSD-DE通道选择算法，首先通过微分进化算法选出通道子集，然后进行CSSD特征提取，最后输入到逻辑线性分类器中进行判别，得出的正则化目标函数值作为评价最优通道子集的标准。要注意只有训练集参与通道选择(避免使用测试集)，并且采用十倍交叉验证，然后将选择的通道子集应用到测试集，最后得到分类结果。实验结果表明：交叉概率选择为0.7时，选择通道数为11，测试集正确率为80%，错误率比使用全部通道子集降低了3%。

为了减少微分进化算法搜索的次数和时间，提出了选择固定通道个数的CSSD-DE2算法。测试集正确率达到了93%，优于竞赛第一名的91%正确率，而且选择通道个数从11个降到了6个，搜索时间也大大地缩短了。

为了对比，将另外两种特征选择算法应用到脑机接口通道选择中。一种是最大相关最小冗余度算法，mRMR在所选通道个数为7至10时，错误率比较接近于所有通道的错误率。一种是支持向量机回归特征消去算法，SVM-RFE在选择较少通道时，错误率并不能明显的减少。这两种算法在通道选择方面的效果都不如CSSD-DE算法令人满意，但有其特点，也值得深入研究。

可以进一步研究其它脑电特征提取方法和通道选择算法的结合，固定通道和随机通道选择策略的区别。这种思想也可以用到其它特征提取和特征选择的混合方法中，也可用到其它生物医学数据或模式分类中。

[1]Wolpaw JR，Birbaumer N，Heetderks WJ.Brain-computer interface technology.A review of the first intermational meeting[J].IEEE Transactions Rehabilitation Engineering，2000，8(2)：164-173.

[2]Toro C，Deuschl G，Thatcher R， et al. Even-related desynchronization and movement related cortical potentials on the ECoG and EEG [ J]. Electronencephalography and ClinicalNeurophysiology，1994，93(5)：380-389.

[3]吕俊，谢胜利.基于运动想象的皮层脑电图频域模式滤波[J].华南理工大学学报(自然科学版)，2008，36(5)：101-103.

[4]Leuthardt E，Schalk G，Wolpaw J，et al.A brain-computer interface using electrocorticographic signals in humans[J].Neural Eng，2004，1：63-71.

[5]Lalt N，Hinterberger T，Widman G，et al.Methods towards invasive human brain computer interface[J].Advances in Neural Information Processing System(NIPS).2005，17：737-744.

[6]Grainmann B，Huggins J，Levine S，et al.Towards a direct brain interface based on human subdural recordings and wavelet packet analysis[J].IEEE Trans Biomed Eng，2004，51：954-962.

[7]刘冲，赵海滨，李春胜，等.基于频带能量归一化和 SVM-RFE的 ECoG 分类[J].仪器仪表学报，2011，32(3)：534-535.

[8]赵海滨，刘冲，喻春阳，等.利用频带能量和k近邻分类器进行皮层脑电图分类[J].计算机应用，2010，30(11)：3105-3106.

[9]毛勇，周晓波，夏铮，等.特征选择算法的研究综述[J].模式识别与人工智能，2007，20(2)：211-218.

[10]Wei Qingguo，Lu Zongwu，Chen Kui，et al.Channel selection for optimizing feature extraction in an electrocorticogram-based braincomputer interface[J].Journal of Clinical Neurophysiology.2010，27(5)：321-326.

[11]吕俊，基于CSP_BPSO的脑-机接口电极选择[J].华南理工大学学报(自然科学版)，2010，38(10)：7-13.

[12]刘冲，李春胜，赵海滨，等.特征选择算法在ECoG分类中的应用[J].东北大学学报(自然科学版)，2011，32(5)：658-660.

[13]刘琳，魏庆国.CSSD+AAR模型在脑电信号处理中的应用[J].通信技术，2008，42(10)：207-209.

[14]苏海军，杨煜普，王宇嘉.微分进化算法的研究综述[J].系统工程与电子技术，2008，30(9)：1793-1796.

[15]赵光权，彭喜元，孙宁.基于混合优化策略的微分进化改进算法[J].电子学报，2006，34(12)：2402-2403.

[16]赵光权，彭喜元，孙宁.带局部增强算子的微分进化改进算法[J].电子学报，2007，35(5)：849-850.

[17]叶柠，孙宇舸，王旭.基于共空间模式和神经元网络的脑 -机接口信号的识别[J].东北大学学报(自然科学版).2010，31(1)：12-15.

[18]唐艳，刘建新，龚安栋.ICA-CSSD的脑机接口分类[J].电子科技大学学报，2008，37(3)：466-467.

[19]Wang Yijun，Zhang Zhiguang，Li Yong.BCI competition 2003-data set IV：an algorithm based on CSSD and FDA for classifying signal-trial EEG[J].IEEE Trans Biomedl Eng，2004，51(6)：1081-1086.

[20]Peng Hanchuan，Long Fuhui，Ding Chris.Feature selection based on mutual information： Titeria of Max-dependency， Max-Relevance，and Min-Redundancy[J].IEEE Trans PatternAnalysis and Machine Intelligence，2005，27(8)：1226-1237.

[21]Peng Hanchuan，Ding Chris，Long Fuhui.Minimum redundancy maximum relevance feature selection[J].IEEE Intelligent Systems，2005，20(6)：70-71.

[22]Guyon I，Weston J，Barnhill S，et al.Gene selection for cancer classification using support vector machines[J]. Machine Learning，2002，46(1-3)：389-422.

[23]游伟，李树涛，谭明奎.基于 SVM-RFE-SFS的基因选择方法[J].中国生物医学工程学报，2010，29(1)：93-95.

[24]Blankertz B，Muller K，Krusienski DJ，et al.The BCI Competition III：Validating Alternative Approaches to Actual BCI Problem[J].IEEE Trans Neural Sys Rehab Eng，2006，14(2)：153-159.

[25]王金甲，李静，张涛，等.二次映射和遗传算法用于鉴别可视化特征提取[J].系统仿真学报.2009，21(6)：5081-5082.